back home
Small-normed projections onto polynomial and
spline spaces
Summary
Small-normed projections onto a 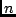 -dimensional subspace
-dimensional subspace 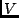 of
of
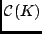 are investigated by way of small-conditioned bases of
are investigated by way of small-conditioned bases of 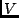 .
The
.
The 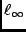 -condition number
-condition number
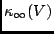 of the space
of the space 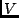 ,
or
its Banach-Mazur distance to
,
or
its Banach-Mazur distance to 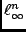 , is shown to equal the
minimal norm of generalized interpolating projections onto
, is shown to equal the
minimal norm of generalized interpolating projections onto 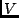 when
when 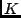 is the interval
is the interval ![$[-1,1]$](img8.png) or the unit circle.
The subsequent inequalities involving the projection constant and the interpolating projection
constant, namely
or the unit circle.
The subsequent inequalities involving the projection constant and the interpolating projection
constant, namely
are studied in details
for some polynomial spaces of low dimension.
For spline spaces, it is relevant to estimate
these projection constants only in terms of the order of the
splines.
For instance, if
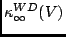 represents the least condition number of a weak Descartes basis of
represents the least condition number of a weak Descartes basis of
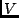 , the inequality
, the inequality
gives the opportunity to bound the
interpolating projection constant of a spline space
by the condition number of the B-spline basis.
In an attempt to
evaluate the latter accurately,
we are led to establish a Markov-type interlacing
property for Chebyshevian B-splines.
More precisely, we prove that if the knots of two Chebyshevian B-splines of
identical support interlace, then the zeros of their appropriate
derivatives also interlace.
As for the projection constant of a spline space, it may be estimated
independently of the underlying knot sequence via the orthogonal projection onto the
space.
Indeed, the supremum over all knot sequences of the max-norm of this projection is
known to be finite,
although the exact value of the supremum, or merely its order, remains to be found.
We make a step in this direction by determining precise bounds of order 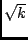 in the cases of continuous and of differentiable splines.
in the cases of continuous and of differentiable splines.
If you wish to obtain the whole dissertation, do contact me at simon.foucart@centraliens.net
and I will e-mail you the pdf file.