Superfluid Vortices

Instructor: Dr Natalia Berloff Office: CMS G1.02 E-mail: N.G.Berloff@damtp.cam.ac.uk Lecture: MR 15 Class web page: www.damtp.cam.ac.uk/user/ngb23/SV/

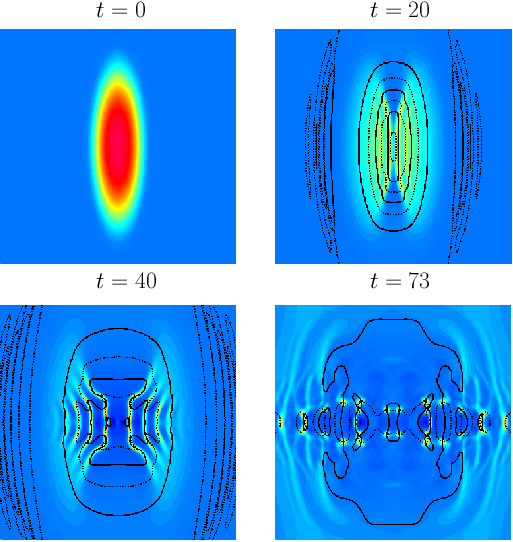
Vortices are often associated with fluid dynamics: in this course we shall concentrate on quantized vortices. These are vortices in nonlinear fields (superfluid flow fields being but one example) that owe their existence and perseverance to the topology of the order-parameter field describing a medium with broken symmetry. The basic Ginzburg-Landau model serves to describe the vortex core structure in systems as diverse as chemical patterns, liquid crystals, atomic condensates, superconductors, and relativistics strings.

Most of the course will be devoted to superfluid motion that, in its simplest form, can be formulated as a conservative dynamical system. At the most basic level, the theory is projected on the classical inviscid compressible fluid dynamics. But it will be shown that acoustic dispersion creates an effective dissipation mechanism, replacing friction, and the latter makes a comeback when more realistic models are considered.

The topics covered are: Introduction to order parameter space, broken symmetry and foundations of topological theory of defects. Dissipative Ginzburg-Landau equations. Vortices in liquid crystals. Vortices in superfluids. Gross-Pitaevskii equation (GPE). Solitary waves of the GPE: vortex rings and rarefaction pulses and their stability. Vortex nucleations. Superfluid helium. Landau two-fluid model and HVBK model. Motion of vortex lines. Dissipative and nonlocal GPE. Vortices in non-uniform Bose-Einstein condensates. Systems with special properties, more intricate topology with applications to superconductors, systems far from equilibrium, cosmic strings etc.

Pre-requisites for the course include previous attendance at a first course in fluid mechanics. Familiarity with solution methods for partial differential equations will be assumed.

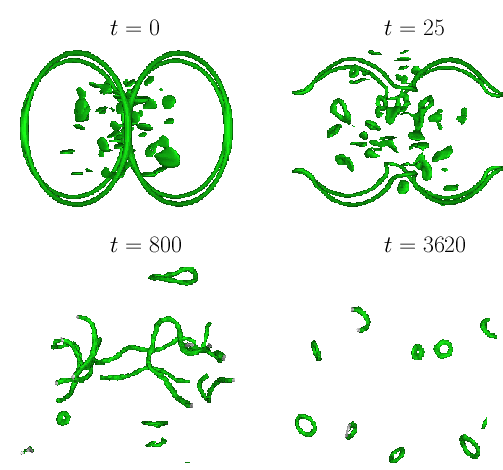
Reading to complement course material L.M. Pismen ``Vortices in nonlinear fields: from liquid crystals to superfluids; from non-equilibrium patterns to cosmic strings'', International series of monographs in physics 100, Clarendon Press Oxford, 1999. R.J. Donnelly: Quantized Vortices in Helium II, Cambridge University Press, Cambridge, 1991. P.H. Roberts and N.G. Berloff, ``Nonlinear Schrodinger equation as a model of superfluid helium,'' "Quantized Vortex Dynamics and Superfluid Turbulence" edited by C.F. Barenghi, R.J. Donnelly and W.F. Vinen, Lecture Notes in Physics, volume 571, Springer-Verlag, 2001. (Available also here ) A.L. Fetter and A.A. Svidzinsky ``Vortices in a trapped dilute Bose-Einstein condensate'', J. Phys.: Condens. Matter 13, R135-R194 (2001).