2 The Hot Universe
As we wind the clock back towards the Big Bang, the energy density in the universe increases. As this happens, particles interact more and more frequently, and the state of the universe is well approximated by a hot fluid in equilibrium. This is sometimes referred to as the primeval fireball of the Big Bang. The purpose of this section is to introduce a few basic properties of this fireball.
It is worth sketching the big picture. First we play the movie in reverse. As we go back in time, the Universe becomes hotter and hotter and things fall apart. Running the movie forward, the Universe cools and various objects form.
For example, there is an important event, roughly 300,000 years after the Big Bang, when atoms form for the first time. Prior to this, the temperature was higher than the 13.6 eV binding energy of hydrogen, and the electrons were stripped from the protons. This moment in time is known as recombination and will be described in Section 2.3. (Obviously a better name would simply be “combination” since the electrons and protons combined for the first time, but we don’t get to decide these things). This is a key moment in the history of the universe. Prior to this time, space was filled with a charged plasma through which light is unable to propagate. But when the electrons and protons form to make (mostly) neutral hydrogen, the universe becomes transparent. The cosmic microwave background, which will be discussed in Section 2.2, dates from this time.
At yet earlier times, the universe was so hot that nuclei fail to cling together and they fall apart into their constituent protons and neutrons. This process – which, running forwards in time is known as nucleosynthesis – happens around 3 minutes after the Big Bang and is understood in exquisite detail. We will describe some of the basic reactions in Section 2.5.3.
As we continue to trace the clock further back, the universe is heated to extraordinary temperatures, corresponding to the energies probed in particle accelerators and beyond. Taking knowledge from particle physics, even here we have a good idea of what happens. At some point, known as the QCD phase transition, protons and neutrons melt, dissolving into a soup of their constituents known as the quark-gluon plasma. Earlier still, at the electroweak phase transition, the condensate of the Higgs boson melts. Beyond this, we have little clear knowledge but there are still other events that we know must occur. The purpose of this chapter is the tell this story.
2.1 Some Statistical Mechanics
Our first task is to build a language that allows us to describe stuff that is hot. We will cherry pick a few key results that we need. A much fuller discussion of the subject can be found in the lectures on Statistical Physics and the lectures on Kinetic Theory.
Ideas such as heat and temperature are not part of the fundamental laws of physics. There is no such thing, for example, as the temperature of a single electron. Instead, these are examples of emergent phenomena, concepts which arise only when a sufficiently large number of particles are thrown together. In domestic situations, where we usually apply these ideas, large means particles. As we will see, in the cosmological setting can be substantially larger.
When dealing with such a large number of particles, we need to shift our point of view. The kinds of things that we usually discuss in classical physics, such as the position and momentum of each individual particle, no longer hold any interest. Instead, we want to know coarse-grained properties of the system. For example, we might like to know the probability that a particle chosen at random has a momentum . In what follows, we call this probability distribution .
Equilibrium
In general, the distribution will be very complicated. But patience brings rewards. If we wait a suitably long time, the individual particles will collide with each other, transferring energy and momentum among themselves until, eventually, any knowledge about the initial conditions is effectively lost. The resulting state is known as equilibrium and is described by a time-independent probability distribution . In equilibrium, the constituent particles are flying around in random directions. But, if you focus only on the coarse-grained probability distribution, everything appears calm.
Equilibrium states are characterised by a number of macroscopic quantities. These will be dealt with in detail in the Statistical Physics course, but here we summarise some key facts.
The most important characteristic of an equilibrium state is temperature. This is related to the average energy of the state in a way that we will make precise below. The reason that temperature plays such an important role is due to the following property: suppose that we have two different systems, each individually in equilibrium, one at temperature and the other at temperature . We then bring the two systems together and allow them to exchange energy. If , then the two systems remain unaffected by this, and the combined system is in equilibrium. In contrast, if , then then a net energy will flow from the hotter system to the colder system, and the combined system will eventually settle down to a new equilibrium state at some intermediate temperature. Two systems which have the same temperature are said to be in thermal equilibrium.
Other kinds of equilibria are also possible. One that we will meet later in this section arises when two systems are able to exchange particles. Often we will be interested in this when one type of particle can transmute into another. In this case, we characterise the system by another quantity known as the chemical potential. (The name comes from chemical reactions although, in this course, will be more interested in processes in atomic or particle physics.) The chemical potential has the property that if two systems have the same value then, when brought together, there will not be a net transfer of particles from one system to the other. In this case, the systems are said to be in chemical equilibrium.
2.1.1 The Boltzmann Distribution
For now we will focus on states in thermal equilibrium. The thermal properties of a state are closely related to its energy which, in turn, is related to the momentum of the constituent particles. This means that understanding thermal equilibrium is akin to understanding the momentum distribution of particles. We will see a number of examples of this in what follows.
A microscopic understanding of thermal equilibrium was first provided by Boltzmann. It turns out that the result is somewhat easier to state in the language of quantum mechanics, although it also applies to the classical world. Consider a system with discrete energy eigenstates , each with energy . In thermal equilibrium at temperature , the probability that the system sits in the state is given by the Boltzmann distribution,
| (2.89) |
Here is the Boltzmann constant, defined to be
This fundamental constant provides a translation between temperatures and energies. Meanwhile is simply a normalisation constant designed to ensure that
This normalisation factor has its own name: it is called the partition function and it plays a starring role in most treatments of statistical mechanics. For our purposes, it will suffice to keep firmly in the background.
It is possible to derive the Boltzmann distribution from more elementary principles. (Such a derivation can be found in the lectures on Statistical Physics.) Here, we will simply take the distribution (2.89) to be the definition of both thermal equilibrium and the temperature.
The Boltzmann distribution gives us some simple intuition for the meaning of thermal equilibrium. We see that the any state with has a more or less equal chance of being occupied, while any state with has a vanishingly small chance of being occupied. In this way sets the characteristic energy scale of the system.
We’ll see many variations of the Boltzmann distribution in what follows. It gets tedious to keep writing . For this reason we define
We will be careless in what follows and also refer to as “temperature”: obviously it is actually (proportional to) the inverse temperature. The Boltzmann distribution then reads
Above, we mentioned the key property of temperature: it determines whether two systems sit in thermal equilibrium. We should check that this is indeed obeyed by the Boltzmann distribution. Suppose that we have two systems, and , both at the same temperature , but with different microscopic constituents, meaning that their energy levels differ. If we bring the two systems together, we expect that the combined system also sits in a Boltzmann distribution at temperature . Happily, this is indeed the case. To see this note that we have independent probability distributions for and , so the combined probability distribution is given by
But this is again of the Boltzmann form. The denominator can be written as
where we recognise this final expression as , the partition function of the combined system . This had to be the case to ensure that the joint probability distribution is correctly normalised.
It’s worth re-iterating what we have learned. You might think that if we combined two systems, separately in equilibrium, then there would be no energy transfer from one to the other if the average energies coincide, i.e. , with
However, this is not the right criterion. As we have seen above, the average energies of the two systems can be very different. It is the temperatures that must coincide.
2.1.2 The Ideal Gas
As our first application of the Boltzmann distribution, consider a gas of non-relativistic particles, each of mass . We will assume that there are no interactions between these particles, so the energy of each is given by
| (2.90) |
Before we proceed, I should mention a subtlety. We’ve turned off interactions in order to make our life simpler. Yet, from our earlier discussion, it should be clear that interactions are crucial if we are ever going to reach equilibrium, since this requires a large number of collisions to share energy and momentum between particles! This is one of many annoying and fiddly issues that plague the fundamentals of statistical mechanics. We will argue this subtlety away by pretending that the interactions are strong enough to drive the system to equilibrium, but small enough to ignore when describing equilibrium. Obviously this is unsatisfactory. We can do better, but it is more work. (See, for example, the discussion of the interacting gas in the lectures on Statistical Physics or the derivation of the approach to equilibrium in the lectures on Kinetic Theory.) We will also see this issue rear its head in a physical context in Section 2.3.4 when we discuss the phenomenon of decoupling in the early universe.
We consider a gas of particles. We’ll assume that each particle is independent of the others, and focus on the state of a just single particle, specified by the momentum or, equivalently, the velocity . If the momentum is continuous (or finely spaced) we should talk about the probability that the velocity lies in some some volume centred around . We denote the probability distribution as . The Boltzmann distribution (2.89) tells us that this is
| (2.91) |
where is a normalisation factor that we will determine shortly.
Our real interest lies in the speed . The corresponding speed distribution is
| (2.92) |
Note that we have an extra factor of when considering the probability distribution over speeds , as opposed to velocities . This reflects the fact that there’s “more ways” to have a high velocity than a low velocity: the factor of is the area of the sphere swept out by a velocity vector .
We require that
Finally, we find the probability that the particle has speed between and to be
| (2.93) |
This is known as the Maxwell-Boltzmann distribution. It tells us the distribution of the speeds of gas molecules in this room.
Pressure and the Equation of State
We can use the Maxwell-Boltzmann distribution to compute the pressure of a gas. The pressure arises from the constant bombardment by the underlying atoms and can be calculated with some basic physics. Consider a wall of area that lies in the -plane. Let denote the density of particles (i.e. where is the number of particles and the volume). In some short time interval , the following happens:
-
•
A particle with velocity will hit the wall if it lies within a distance of the wall and if it’s travelling towards the wall, rather than away. The number of such particles with velocity centred around is
with a factor of picking out only those particles that travel in the right direction.
-
•
After each such collision, the momentum of the particle changes from to , with and left unchanged. As before, this holds only for the initial . We therefore write the impulse imparted by each particle as .
-
•
This impulse is equated with where is the force on the wall. The force arising from particles with velocity in the region about is
where we dropped the modulus signs on the grounds that the sign of the momentum is the same as the sign of the velocity .
-
•
The pressure on the wall is the force per unit area, . We learn that the pressure from those particles with velocity in the region of is
At this stage we invoke isotropy of the gas, which means that . We therefore have
(2.94)
The last stage is to integrate over all velocities, weighted with the probability distribution. In the final form (2.94), the pressure is related to the speed rather than the (component of the) velocity . This means that we can use the Maxwell-Boltzmann distribution over speeds (2.93) and write
| (2.95) |
This coincides with our earlier result (1.33) (albeit using slightly different notation for the probability distributions).
The expression (2.95) holds for both relativistic and non-relativistic systems, a fact that we will make use of later. For now, we care only for the non-relativistic case with . Here we have
The integral is straightforward: it is given by
Using this, we find a familiar friend
This is the equation of state for an ideal gas.
We can also calculate the average kinetic energy. If the gas contains particles, the total energy is
| (2.96) |
This confirms the result (1.37) that we met when we first introduced non-relativistic fluids.
2.2 The Cosmic Microwave Background
The universe is bathed in a sea of thermal radiation, known as the cosmic microwave background, or the CMB. This was the first piece of evidence for the hot Big Bang – the idea that the early universe was filled with a fireball – and remains one of the most compelling. In this section, we describe some of the basic properties of this radiation.
2.2.1 Blackbody Radiation
To start, we want to derive the properties of a thermal gas of photons. Such a gas in known, unhelpfully, as blackbody radiation.
The state of a single photon is specified by its momentum , with the wavevector. The energy of the photon is given by
where is the (angular) frequency of the photon.
Blackbody radiation comes with a new conceptual ingredient, because the number of photons is not a conserved quantity. This means that when considering the possible states of the gas, we should include states with an arbitrary number of photons. We do this by stating how many photons sit in the state .
In thermal equilibrium, we will not have a definite number of photons , but rather some probability distribution over the number of photons, Focussing on a fixed state , the average number of particles is dictated by the Boltzmann distribution
We can easily do both of these sums. Defining , the partition function is given by
Meanwhile the numerator of takes the form
We learn that the average number of particles with momentum is
| (2.97) |
For , the number of photons is exponentially small. In contrast, when , the number of photons grows linearly as .
Density of States
Our next task is to determine the average number of photons with given energy . To do this, we must count the number of states which have energy .
It’s easier to count objects that are discrete rather than continuous. For this reason, we’ll put our system in a square box with sides of length . At the end of the calculation, we can happily send . In such a box, the wavevector is quantised: it takes values
This is true for both a classical wave or a quantum particle; in both cases, an integer number of wavelengths must fit in the box.
Different states are labelled by the integers . When counting, or summing over such states, we should therefore sum over the . However, for very large boxes, so that is much bigger than any other length scale in the game, we can approximate this sum by an integral,
| (2.98) |
where is the volume of the box. The formula above counts all states. But the final form has a simple interpretation: the number of states with the magnitude of the wavevector between and is . Note that the term is reminiscent of the term that appeared in the Maxwell-Boltzmann distribution; both have the same origin.
We would like to compute the number of states with frequency between and . For this, we simply use
This tells us that the number of states with frequency between and is .
There is one final fact that we need. Photons come with two polarisation states. This means that the total number of states is twice the number above. We can now combine this with our earlier result (2.97). In thermal equilibrium, the average number of photons with frequency between and is
We usually write this in terms of the number density . Moreover, we will be a little lazy and drop the expectation value signs. The distribution of photons in a thermal bath is then written as
| (2.99) |
This is the Planck blackbody distribution. For a fixed temperature, , the distribution tells us how many photons of a given frequency – and hence, of a given colour – are present. The distribution peaks in visible light for temperatures around K, which is the temperature of the surface of the Sun. (Presumably the Sun evolved to be at exactly the right temperature so that our eyes can see it. Or something.)
The Equation of State
We now have all the information that we need to compute the equation of state. First the energy density. This is straightforward: we just need to integrate
| (2.100) |
Next the pressure. We can import our previous formula (2.95), now with . But this gives precisely the same integral as the energy density; it differs only by the overall factor of ,
This, of course, is the relativistic equation of state that we used when describing the expanding universe.
Finally, we can actually do the integral (2.100). In fact, there’s a couple of quantities of interest. The energy density is
Meanwhile, the total number density is
Both of these integrals take a similar form. Here we just quote the general result without proof:
| (2.101) |
The Gamma function is the analytic continuation of the factorial function to the real numbers; when evaluated on the integers it gives . Meanwhile, the Riemann zeta function is defined, for , as . It turns out that , giving us . In contrast, there is no such simple expression for . It is sometimes referred to as Apéry’s constant. A derivation of (2.101) can be found in Section 3.5.3 of the lectures on Statistical Physics.
We learn that the energy density is
| (2.102) |
Meanwhile, the total number density is
| (2.103) |
Notice, in particular, that the number density of photons varies with the temperature. This will be important in what follows.
2.2.2 The CMB Today
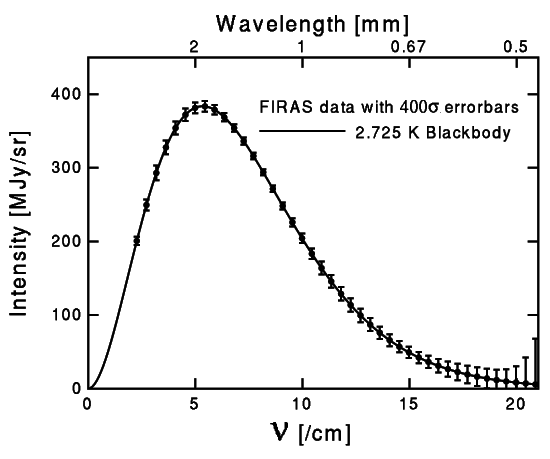
The universe today is filled with a sea of photons, the cosmic microwave background. This is the afterglow of the fireball that filled the universe in its earliest moments. The frequency spectrum of the photons is a perfect fit to the blackbody spectrum, with at a temperature
| (2.104) |
This spectrum is shown in Figure 29. There are small, local deviations in this temperature at the level of
These fluctuations will be discussed further in Section 3.4.
From the temperature (2.104), we can determine the energy density and number density in photons. From (2.102), the energy density is given by
We can compare this to the critical energy density (1.69), to find
This is the value (1.68) that we quoted previously. There are, of course, further photons in starlight, but they are dwarfed in both energy and number by the CMB.
From (2.103), the number density of CMB photons is
We can compare this to the number of baryons (i.e. protons and neutrons). The density of baryons is (1.72) , so the total mass in baryons is
The mass of the proton and neutron are roughly the same, at . This places the number density of baryons as
We see that there are many more photons in the universe than baryons: the ratio is
| (2.105) |
This is one of the fundamental numbers in cosmology. As we will see, this ratio has been pretty much constant since the first second or so after the Big Bang and plays a crucial role in both nucleosynthesis (the formation of heavier nuclei) and in recombination (the formation of atoms). We do not, currently, have a good theoretical understanding of where this number fundamentally comes from: it is something that we can only derive from observation.
The CMB is a Relic
There is an important twist to the story above. We have computed the expected distribution of photons in thermal equilibrium, and found that it matches perfectly with the spectrum of the cosmic microwave background. The twist is that the CMB is not in equilibrium!
Recall that equilibrium is a property that arises when particles are constantly interacting. Yet the CMB photons have barely spoken to anyone for the past 13 billion years. The occasional photon may bump into a planet, or an infra-red detector fitted to a satellite, but most just wend their merry way through the universe, uninterrupted.
How then did the CMB photons come to form a perfect equilibrium spectrum? The answer is that this dates from a time when the photons were interacting frequently with matter. Fluids like this, that have long since fallen out of thermal equilibrium, but nonetheless retain their thermal character, are called relics.
There are a couple of questions that we would like to address. The first is: when were the photons last interacting and, hence, last genuinely in equilibrium? This is called the time of last scattering, and we will compute it in Section 2.3 below. The second question is: what happened to the distribution of photons subsequently?
We start by answering the second of these questions. Once the photons no longer interact, they are essentially free particles. As the universe expands, each photon is redshifted as explained in Section 1.1.3. This means that the wavelength is stretched and, correspondingly, the frequency is decreased as the universe expands.
| (2.106) |
At the same time, the number of photons is diluted by a factor of as the universe expands. Putting these two effects together, an initial blackbody distribution (2.99) will, if left alone, evolve as
The dilution factor is absorbed into the frequency in the and terms. But not in the exponent. However, the resulting distribution can be put back into blackbody form if we think of the temperature as time dependent
where the , with the time varying temperature
| (2.107) |
We see that, left alone, a blackbody distribution will keep the same overall form, but with the temperature scaling as .
This means that, if we can figure out the temperature when the photons were last in equilibrium, then we can immediately determine the redshift at which this occurred . We’ll compute both of these in Section 2.3.
2.2.3 The Discovery of the CMB
In 1964, two radio astronomers, Arno Penzias and Robert Wilson, got a new toy. The microwave horn antenna was originally used by their employers, the Bell telephone company, for satellite communication. Now Penzias and Wilson hoped to do some science with it, measuring the radio noise emitted in the direction away from the plane of the galaxy.
To their surprise, they found a background noise which did not depend on the direction in which they pointed their antenna. Nor did it depend on the time of day or the time of a year. Taken seriously, this suggested that the noise was a message from the wider universe.

There was, however, an alternative, more mundane explanation. Maybe the noise was coming from the antenna itself, some undiscovered systematic effect that they had failed be take into account. Indeed, they soon found a putative source of the noise: a pair of pigeons had taken roost and deposited what Penzias called “a white dielectric material” over much of the antenna. They removed this material (and shot the pigeons), but the noise remained. What Penzias and Wilson had on their hands was not pigeon shit, but one of the great discoveries of the twentieth century: the afterglow of the Big Bang itself, with a temperature that they measured to lie between 2.5 K and 4.5 K. In 1965 they published their result with the attention-grabbing title: “A Measurement of Excess Antenna Temperature at 4080 Mc/s”.
Penzias and Wilson were not unaware of the significance of their finding. In the year since they first found the noise, they had done what good scientists should always do: they talked to their friends. They were soon put in touch with the group in nearby Princeton where Jim Peebles, a theoretical cosmologist, had recently predicted a background radiation with a temperature of a few degrees, based on the idea of nucleosynthesis in the very early universe (an idea we will describe in Section 2.5.3). Meanwhile, three experimental colleagues, Dicke, Roll and Wilkinson had cobbled together a small antenna in the hope of searching for this radiation. These four scientists wrote a companion paper, outlining the importance of the discovery. In 1978, Penzias and Wilson were awarded the Nobel prize. It took another 39 years before Peebles gained the same recognition.
In fact there had been earlier predictions of the CMB. In the 1940s, Gammow together with Alpher and Herman suggested that the early universe began only with neutrons and, through somewhat dodgy calculations, concluded that there should be a background radiation at 5 K. Later other scientists, including Zel’dovich in the Soviet Union, and Hoyle and Taylor in England, used nucleosynthesis to predict the existence of the CMB at a few degrees. Yet none of these results were taken sufficiently seriously to search for the signal before Penzias and Wilson made their serendipitous discovery.
Detecting the CMB was just the beginning of the story. The radiation is not, it turns out, perfectly uniform but contains small anisotropies. These contain precious information about the make-up of the universe when it was much younger. A number of theorists, including Harrison, Zel’dovich, and Peebles and Yu, predicted that these anisotropies could be observed at a level of to . These were finally detected by the NASA COBE satellite in the early 1990s. Since then a number of ground based telescopes, including BOOMERanG and MAXIMA, and a two full sky maps from the satellites WMAP and Planck, have mapped out the CMB in exquisite detail. We will describe these anisotropies in Section 3.
2.3 Recombination
We’ve learned that the CMB is a relic, with its perfect blackbody spectrum a remnant of an earlier, more intense time in the universe, when the photons were in equilibrium with matter. We would like to gain a better understanding of this time.
Photons interact with electric charge. Nowadays, the vast majority of matter in the universe is in the form of neutral atoms, and electrons interact only with the charged constituents of the atoms. Such interactions are relatively weak. However, there was a time in the early universe when the temperature was so great that electrons and protons could no longer bind into neutral atoms. Instead, the universe was filled with a plasma. In this era, the matter and photons interacted strongly and were in equilibrium.
The CMB that we see today dates from this time. Or, more precisely, from the time when electrons and protons first bound themselves into neutral hydrogen, emitting a photon in the process
| (2.108) |
The moment at which this occurs is called recombination. As the arrows illustrate, this process can happen in both directions.
Interactions like (2.108) involve one particle type transmuting into a different type. This means that the number of, say, hydrogen atoms is not fixed but fluctuating. We need to introduce a new concept that allows us to deal with such situations. This concept is the chemical potential.
2.3.1 The Chemical Potential
The chemical potential offers a slight generalisation of the Boltzmann distribution which is useful in situations where the number of particles in a system is not fixed. It was, as the name suggests, originally introduced to describe chemical reactions but we will re-purpose it to describe atomic reactions like (2.108) (and, later, nuclear reactions).
Although our ultimate goal is to describe atomic reactions, we can first introduce the chemical potential in a more mundane setting. Suppose that we have a fixed number of atoms in a box of size . If we focus attention on some large, fixed sub-volume , then we would expect the gas in to share the same macroscopic properties, such as temperature and pressure, as the whole gas in . But particles can happily fly in and out of and the total number in this region is not fixed. Instead, there is some probability distribution which has the property that the average number density coincides with .
In this situation, it’s clear that we should consider states of all possible particle number in . There is a possibility, albeit a very small one, that contains no particles at all. There is also a small possibility that it contains all the particles.
If we work in the language of quantum mechanics, each state in the system can be assigned both an energy and a particle number . Correspondingly, equilibrium states are characterised by two macroscopic properties: the temperature and the chemical potential . These are defined through the generalised Boltzmann distribution
| (2.109) |
where is again the appropriate normalisation factor. In the language of statistical mechanics, this is referred to as the grand canonical ensemble.
Clearly, the distribution has the same exponential form as the Boltzmann distribution. This is important. We learned in Section 2.1.1 that two isolated systems which sit at the same temperature will remain in thermal equilibrium when brought together, meaning that there will be no transfer of energy from one system to the other. Exactly the same argument tells us that if two isolated systems have the same chemical potential then, when brought together, there will be no net flux of particles from one system to the other. In this case, we say that the systems are in chemical equilibrium.
Notice that the requirement for equilibrium is not that the number densities of the systems are equal: it is the chemical potentials that must be equal. This is entirely analogous to the statement that it is temperature, rather than energy density, that determines whether systems are in thermal equilibrium.
We’ll see examples of how to wield the chemical below, but before we do it’s worth mentioning a few issues.
-
•
In general, we can introduce a different chemical potential for every conserved quantity in the system. This is because conserved quantities commute with the Hamiltonian, and so it makes sense to label microscopic states by both the energy and a further quantum number. One familiar example is electric charge . Here, the corresponding chemical potential is voltage.
This leads to an almost-contradictory pair of statements. First, we can only introduce a chemical potential for any conserved quantity. Second, the purpose of the chemical potential is to allow this conserved quantity to fluctuate! If you’re confused about this, then think back to the volume , or to the meaning of voltage in electromagnetism, both of which give examples where these statements hold.
-
•
The story above is very similar to our derivation of the Planck blackbody distribution for photons. There too we labeled states by both energy and particle number, but we didn’t introduce a chemical potential. What’s different now? This is actually a rather subtle issue. Ultimately it is related to the fact that we ignore interactions while simultaneously pretending that they are crucial to reach equilibrium. As soon as we take these interactions into account, the number of photons is not conserved so we can’t label states by both energy and photon number. This is what prohibits us from introducing a chemical potential for photons. In contrast, we can introduce a chemical potential in situations where particle number (or some other quantity) is conserved even in the presence of interactions.
2.3.2 Non-Relativistic Gases Revisited
For our first application of the chemical potential, we’re going to re-derive the ideal gas equation. At first sight, this will appear to be only a more complicated derivation of something we’ve seen already. The pay-off will come only in Section 2.3.3 where we will understand recombination and the atomic reaction (2.108).
We consider non-relativistic particles, with energy
As with our calculation of photons, we now consider states that have arbitrary numbers of particles. We choose to specify these states by stating how many particles have momentum . For each choice of momentum, the number of particles77 7 Actually, there is a subtlety here: I am implicitly assuming that the particles are bosons. We’ll look at this more closely in Section 2.4. can be . The generalised Boltzmann distribution (2.109) then tells us that the average number of particles with momentum is
where the normalisation factor (or, in fancy language, the grand canonical partition function) is given by the geometric series
This is exactly the same calculation as we saw for photons in Section 2.2.1, but with the additional minor complication of a chemical potential. Note that computing allows us to immediately determine the expected number of particles since we can write
| (2.110) |
This is known as the Bose-Einstein distribution and will be discussed further in Section 2.4.
To compute the average total number of particles, we simply need to integrate over all momenta . We must include the density of states, but this is identical to the calculation we did for photons, with the result (2.98). The total average number of particles is then
where we’ve been a little lazy and dropped the brackets on . We usually write this in terms of the particle density ,
| (2.111) |
where, in the second equality, we have chosen to integrate using spherical polar coordinates, picking up a factor of from the angular integrals and a factor of in the Jacobian for our troubles. We have also used the explicit expression for the energy in the distribution.
At this stage, we have an annoying looking integral to do. To proceed, let’s pick a value of the chemical potential such that . (We’ll see what this means physically below.) We can then drop the in the denominator and approximate the integral as
| (2.112) |
Let’s try to interpret this. Read naively, it seems to tell us that the number density of particles depends on the temperature. But that’s certainly not what happens for the gas in this room, where and depend on temperature but the number density is fixed. We can achieve this by taking the chemical potential to also depend on temperature. Specifically, we wish to describe a gas with fixed , then we simply invert the equation above to get an expression for the chemical potential
| (2.113) |
Before we proceed, we can use this result to understand what the condition , that we used to do the integral, is forcing upon us. Comparing to the expression above, it says that the number density is bounded above by
This is sensible. It’s telling us that the ideal gas can’t be too dense. In particular, the average distance between particles should be much larger than the length scale set by . This is the average de Broglie wavelength of particles at temperature . If is increased so that the separation between particles is comparable to then quantum effects kick in and we have to return to our original integral (2.111) and make a different approximation to do the integral and understand the physics. (This path will lead to the beautiful phenomenon of Bose-Einstein condensation, but it is a subject for a different course.)
So far, the chemical potential has not bought us anything new. We have simply recovered old results in a slightly more convoluted framework in which the number of particles can fluctuate. But, as we will now see, this is exactly what we need to deal with atomic reactions.
2.3.3 The Saha Equation
We would like to consider a gas of electrons and protons in equilibrium at some temperature. They have the possibility to combine and form hydrogen, which we will think of as an atomic reaction, akin to the chemical reactions that we met in school. It is
The question we would like to ask is: what proportion of the particles are hydrogen, and what proportion are electron-proton pairs?
To simplify life, we will assume that the hydrogen atom forms in its ground state, with a binding energy
In fact, this turn out to be a bad assumption! We explain why at the end of this section.
Naively, we would expect hydrogen to ionize when we reach temperatures of . It’s certainly true that for temperature , the electrons can no longer cling on to the protons, and any hydrogen atom is surely ripped apart. However, it will ultimately turn out that hydrogen only forms at temperatures significantly lower than .
We’ll treat each of the massive particles – the electron, proton and hydrogen atom – in a similar way to the non-relativistic gas that we met in Section 2.3.2. There will, however, be two differences. First, we include the rest mass energy of the atoms, so each particle has energy
This will be useful as we can think of the binding energy as the mass difference
| (2.114) |
Secondly, each of our particles comes with a number of internal states. The electron and proton each have corresponding to the two spin states, referred to as “spin up” and “spin down”. (These are analogous to the two polarisation states of the photon that we included when discussing blackbody radiation.) For hydrogen, we have ; the electron and proton spin can either be aligned, to give a spin 0 particle, or anti-aligned to give 3 different spin 1 states.
With these two amendments, our expression for the number density (2.112) of the different species of particles is given by
| (2.115) |
Note that the rest mass energy in the energy can be absorbed by a constant shift of the chemical potential.
Now we can use the chemical potential for something new. We require that these particles are in chemical equilibrium. This means that there is no rapid change from pairs into hydrogen, or vice versa: the numbers of electrons, protons and hydrogen are balanced. This is ensured if the chemical potentials are related by
| (2.116) |
This follows from our original discussion of what it means to be in chemical equilibrium. Recall that if two isolated systems have the same chemical potential then, when brought together, there will be no net flux of particles from one system to the other. This mimics the statement about thermal equilibrium, where if two isolated systems have the same temperature then, when brought together, there will be no net flux of energy from one to the other.
There is no chemical potential for photons because they’re not conserved. In particular, in addition to the reaction there can also be reactions in which the binding results in two photons, , which is ultimately why it makes no sense to talk about a chemical potential for photons. (Some authors write this, misleadingly, as .)
We can use the condition for chemical equilibrium (2.116) to eliminate the chemical potentials in (2.115) to find
| (2.117) |
In the pre-factor, it makes sense to approximate . However, in the exponent, the difference between these masses is crucial; it is the binding energy of hydrogen (2.114). Finally, we use the observed fact that the universe is electrically neutral, so
We then have
| (2.118) |
This is the Saha equation.
Our goal is to understand the fraction of electron-proton pairs that have combined into hydrogen. To this end, we define the ionisation fraction
where, in the second equality, we’re ignoring neutrons and higher elements. (We’ll see in Section 2.5.3 that this is a fairly good approximation.) Since , if it means that all the electrons are free. If , it means that only 10% of the electrons are free, the remainder bound inside hydrogen.
Using , we have and so
The Saha equation gives us an expression for . But to translate this into the fraction , we also need to know the number of baryons. This we take from observation. First, we convert the number of baryons into the number of photons, using (2.105),
Here we need to use the fact that has remained constant since recombination. Next, we use the fact that photons sit at the same temperature as the electrons, protons and hydrogen because they are all in equilibrium. This means that we can then use our earlier expression (2.103) for the number of photons
Combining these gives our final answer
| (2.119) |
Suppose that we look at temperature , which is when we might naively have thought recombination takes place. We see that there are two very small numbers in the game: the factor of and , where the electron mass is . These ensure that at , the ionisation fraction is very close to unity. In other words, nearly all the electrons remain free and unbound. In large part this is of the enormous number of photons, which mean that whenever a proton and electron bind, one can still find sufficient high energy photons in the tail of the blackbody distribution to knock them apart.
Recombination only takes place when the factor is sufficient to compensate both the and factors. Clearly recombination isn’t a one-off process; it happens continuously as the temperature varies. As a benchmark, we’ll calculate the temperature when , so 90% of the electrons are sitting happily in their hydrogen homes. From (2.119), we learn that this occurs when , or
This corresponds to a redshift of
This is significantly later than matter-radiation equality which, as we saw in (1.71), occurs at . This means that, during recombination, the universe is matter dominated, with . We can therefore date the time of recombination to,
After recombination, the constituents of the universe have been mostly neutral atoms. Roughly speaking this means that the universe is transparent and photons can propagate freely. We will look more closely at this statement a little more closely below.
Mea Culpa
The full story is significantly more complicated than the one told above. As we have seen, at the time of recombination the temperature is much lower than the 13.6 eV binding energy of the 1s state of hydrogen. This means that whenever a 1s state forms, it emits a photon which has significantly higher energy that the photons in thermal bath. The most likely outcome is that this high energy photon hits a different hydrogen atom, splitting it into its constituent proton and electron, resulting in no net change in the number of atoms! Instead, recombination must proceed through a rather more tortuous route.
The hydrogen atom doesn’t just have a ground state: there are a whole tower of excited states. These can form without emitting a high energy photon and, indeed, at these low temperatures the thermal bath of photons is in equilibrium with the tower of excited states of hydrogen. There are then two, rather inefficient processes, which populate the 1s state. The 2s state decays down to 1s by emitting two photons (to preserve angular momentum), neither of which have enough energy to re-ionize other atoms. Alternatively, the 2p state can decay to 1s, emitting a photon whose energy is barely enough to excite another hydrogen atom out of the ground state. If this photon experiences redshift, then it can no longer do the job and we increase the number of atoms in the ground state. More details can be found in the book by Weinberg. These issues do not greatly change the values of and that we computed above.
2.3.4 Freeze Out and Last Scattering
Photons interact with electric charge. After electrons and protons combine to form neutral hydrogen, the photons scatter much less frequently and the universe becomes transparent. After this time, the photons are essentially decoupled.
Similar scenarios play out a number of times in the early universe: particles, which once interacted frequently, stop talking to their neighbours and subsequently evolve without care for what’s going on around them. This process is common enough that it is worth exploring in a little detail. As we will see, at heart it hinges on what it means for particle to be in “equilibrium”.
Strictly speaking, an expanding universe is a time dependent background in which the concept of equilibrium does not apply. In most situations, such a comment would be rightly dismissed as the height of pedantry. The expansion of the universe does not, for example, stop me applying the laws of thermodynamics to my morning cup of tea. However, in the very early universe this can become an issue.
For a system to be in equilibrium, the constituent particles must frequently interact, exchanging energy and momentum. For any species of particle (or pair of species) we can define the interaction rate . A particle will, on average, interact with another particle in a time . It makes sense to talk about equilibrium provided that the universe hasn’t significantly changed in the time . The expansion of the universe is governed by the Hubble parameter, so we can sensibly talk about equilibrium provided
In contrast, if then by the time particles interact the universe has undergone significant expansion. In this case, thermal equilibrium cannot be maintained.
For many processes, both the interaction rate and temperature scale with , but in different ways. The result is that particles retain equilibrium at early times, but decouple from the thermal bath at late time. This decoupling occurs when and is known as freeze out.
We now apply these ideas to photons, where freeze out also goes by the name of last scattering. In the early universe, the photons are scattered primarily by the electrons (because they are much lighter than the protons) in a process known as Thomson scattering
The scattering is elastic, meaning that the energy, and therefore the frequency, of the photon is unchanged in the process. For Thomson scattering, the interaction rate is given by
where is the cross-section, a quantity which characterises the strength of the scattering. We computed the cross-section for Thomson scattering in the lectures on Electromagnetism (see Section 6.3.1 of these lectures) where we showed it was given by
Note the dependence on the electron mass ; the corresponding cross-section for scattering off protons is more than a million times smaller.
Last scattering occurs at the temperature such that . We can express the interaction rate by replacing the number density of electrons with the number density of photons,
| (2.120) |
Meanwhile, we can trace back the current value of the Hubble constant, through the matter dominated era, to last scattering. Meanwhile, to compute , we use the formula (1.66)
Evaluated at recombination, radiation, curvature and the cosmological constant are all irrelevant, and this formula becomes
Using the fact that temperature scales as , we then have
Equating this with (2.120) gives
Using (2.119) to solve for (which is a little fiddly) we find that photons stop interacting with matter only when
We learn that the vast majority of electrons must be housed in neutral hydrogen, with only 1% of the original electrons remaining free, before light can happily travel unimpeded. This corresponds to a temperature
and, correspondingly, a time somewhat after recombination,
After this time, the universe becomes transparent. The cosmic microwave background is a snapshot of the universe from this time.
2.4 Bosons and Fermions
To better understand the physics of the Big Bang, there is one last topic from statistical physics that we will need to understand. This follows from a simple statement: quantum particles are indistinguishable. It’s not just that the particles look the same: there is a very real sense in which there is no way to tell them apart.
Consider a state with two identical particles. Now swap the positions of the particles. This doesn’t give us a new state: it is exactly the same state as before (at least up to a minus sign). This subtle effect plays a key role in thermal systems where we’re taking averages over different states. The possibility of a minus sign is important, and means that quantum particles come in two different types, called bosons and fermions.
Consider a state with two identical particles. These particles are called bosons if the wavefunction is symmetric under exchange of the particles.
The particles are fermions if the wavefunction is anti-symmetric
Importantly, if you try to put two fermions on top of each other then the wavefunction vanishes: . This is a reflection of the Pauli exclusion principle which states that two or more fermions cannot sit in the same state. For both bosons and fermions, if you do the exchange twice then you get back to the original state.
There is a deep theorem – known as the spin-statistics theorem – which states that the type of particle is determined by its spin (an intrinsic angular momentum carried by elementary particles). Particles that have integer spin are bosons; particles that have half-integer spin are fermions.
Examples of spin particles, all of which are fermions, include the electron, the various quarks, and neutrinos. Furthermore, protons and neutrons (which, roughly speaking, consist of three quarks) also have spin and so are fermions.
The most familiar example of a boson is the photon. It has spin 1. Other spin 1 particles include the W and Z-bosons (responsible for the weak nuclear force) and gluons (responsible for the strong nuclear force). The only elementary spin 0 particle is the Higgs boson. Finally, the graviton has spin 2 and is also a boson.
While this exhausts the elementary particles, the ideas that we develop here also apply to composite objects like atoms. These too are either bosons or fermions. Since the number of electrons is always equal to the number of protons, it is left to the neutrons to determine the nature of the atom: an odd number of neutrons and it’s a fermion; an even number and it’s a boson.
2.4.1 Bose-Einstein and Fermi-Dirac Distributions
The generalised Boltzmann distribution (2.109) specifies the probability that we sit in a state with some fixed energy and particle number .
In what follows, we will restrict attention to non-interacting particles. In this case, there is a simple way to construct the full set of states starting from the single-particle Hilbert space. The state of a single particle is specified by its momentum . (There may also be some extra, discrete internal degrees of freedom like polarisation or spin; we’ll account for these later.) We’ll denote this single particle state as . For a relativistic particle, the energy is
| (2.121) |
To specify the full multi-particle state , we need to say how many particles occupy the state . The possible values of depend on whether the underlying particle is a boson or fermion:
In our previous discussions of blackbody radiation in Section 2.2.1 and the non-relativistic gas in Section 2.3.2, we did the counting appropriate for bosons. This is fine for blackbody radiation, since photons are bosons, but was an implicit assumption in the case of a non-relativistic gas.
The other alternative is a fermion. For these particles, the Pauli exclusion principle says that a given single-particle state is either empty or occupied. But you can’t put more than one fermion there. This is entirely analogous to the way the periodic table is constructed in chemistry, by filling successive shells, except now the states are in momentum space. (A better analogy is the way a band is filled in solid state physics as described in the lectures on Quantum Mechanics.) For bosonic particles, there is no such restriction: you can pile up as many as you like.
Now we can compute some quantities, like the average particle number and average energy. We deal with bosons and fermions in turn
For bosons, the calculation is exactly the same as we saw in Section 2.3.2. For a given momentum , the average number of photons is
where the normalisation factor is given by the geometric series
As in the previous section, we will be a little lazy and drop the expectation value, so . Then we have
| (2.122) |
This is known as the Bose-Einstein distribution.
For fermions, the calculation is easier still. We can have only or 1 particles in a given state so the average occupation number is
Again, keeping the expectation value signs implicit, we have
| (2.123) |
This is the Fermi-Dirac distribution.
For both bosons and fermions, the calculation of the density of states (2.98) proceeds as before, so that if we integrate over all possible momenta, it should be weighted by
with the pre-factor telling us how quantum states are in a small region .
If we include the degeneracy factor , which tells us the number of internal states of the particle, the number density is given by
| (2.124) |
Similarly, the energy density is
| (2.125) |
and the pressure (2.95) is
| (2.126) |
We’ll now apply these in various examples.
The Non-Relativistic Gas Yet Again
In Section 2.3.2, we computed various quantities of a non-relativistic gas, so that the energy of each particle is
When we evaluated various quantities using the chemical potential approach, we implicitly assumed that the constituent atoms of the gas were bosons so, for example, our expression for the expression for the number density (2.111),
If, instead, we have a gas comprising of fermions then we should replace this expression with
We can then ask: how does the physics change?
If we focus on the high temperature regime of non-relativistic gases, the answer to this question is: very little! This is because we evaluate these integrals using the approximation , and we can immediately drop the in the denominator. This means that both bosons and fermions give rise to the same ideal gas equation.
We do start to see small differences in the behaviour of the gases if we expand the integrals to the next order in . We see much larger differences if we instead study the integrals in a very low-temperature limit. These stories are told in the lectures on Statistical Physics but they hold little cosmological interest.
Instead, the difference between bosons and fermions in cosmology is really only important when we turn to very high temperatures, where the gas becomes relativistic.
2.4.2 Ultra-Relativistic Gases
As we will see in the next section, as we go further back in time, the universe gets hot. Really hot. For any particle, there will be a time such that
In this regime, particle-anti-particle pairs can be created in the fireball. When this happens, both the mass and the chemical potential are negligible. We say that the particles are ultra-relativistic, with their energy given approximately as
just as for a massless particle. We can use our techniques to study the behaviour of gases in this regime.
We start with ultra-relativistic bosons. We work with vanishing chemical potential, . (This will ensure that we have equal numbers of particles an anti-particles. The presence of a chemical potential results in a preference for one over the other, and will be explored in Examples Sheet 3.) The integral (2.124) for the number density gives
while the energy density is
where we’ve used the definition (2.101) of the integral
In both cases, the integrals coincide with those that we met for blackbody radiation
Meanwhile, for fermions we have
and
where, this time, we get the integral
The upshot of these calculations is that the number density is
and the energy density is
The differences are just small numerical factors but, as we will see, these become important in cosmology.
Ultimately, we will be interested in gases that contain many different species of particles. In this case, it is conventional to define the effective number of relativistic species in thermal equilibrium as
| (2.127) |
As the temperature drops below a particle’s mass threshold, , this particle is removed from the sum. In this way, the number of relativistic species is both time and temperature dependent. The energy density from all relativistic species is then written as
| (2.128) |
To calculate in different epochs, we need to know the matter content of the Standard Model and, eventually, the identity of dark matter. We’ll make a start on this in the next section.
2.5 The Hot Big Bang
We have seen that for the first 300,000 years or so, the universe was filled with a fireball in which photons were in thermal equilibrium with matter. We would like to understand what happens to this fireball as we dial the clock back further. This collection of ideas goes by the name of the hot Big Bang theory.
2.5.1 Temperature vs Time
It turns out, unsurprisingly, that the fireball is hotter at earlier times. This is simplest to describe if we go back to when the universe is radiation dominated, at or . Here, the energy density scales as (1.41),
We can compare this to the thermal energy density of photons, given by (2.102)
To see that the temperature scales inversely with the scale factor
| (2.129) |
This is the same temperature scaling that we saw for the CMB after recombination (2.107). Indeed, the underlying arguments are also the same: the energy of each photon is blue-shifted as we go back in time, while their number density increases, resulting in the behaviour. The difference is that now the photons are in equilibrium. If they are disturbed in some way, they will return to their equilibrium state. In contrast, if the photons are disturbed after recombination they will retain a memory of this.
What happens during the time , before recombination but when matter was the dominant energy component? First consider a universe with only non-relativistic matter, with number density . The energy density is
The first term drives the expansion of the universe and is independent of temperature. The second term, which we completely ignored in Section 1 on the grounds that it is negligible, depends on temperature. This was computed in (2.96) and is given by .
As the universe expands, the velocity of non-relativistic particles is red-shifted as . (This is hopefully intuitive, but we have not actually demonstrated this previously. We will derive this redshift in Section 3.1.3.) This means that, in a universe with only non-relativistic matter, we would have
So what happens when we have both matter and radiation? We would expect that the temperature scaling sits somewhere between and . In fact, it is entirely dominated by the radiation contribution. This can be traced to the fact that there are many more photons that baryons; . A comparable ratio is expected to hold for dark matter. This means that the photons, rather than matter, dictate the heat capacity of the thermal bath. The upshot is that the temperature scales as throughout the period of the fireball. Moreover, as we saw in Section 2.2, the temperature of the photons continues to scale as even after they decouple.
Doing a Better Job
The formula gives us an approximate scaling. But we can do better.
We start with the continuity equation (1.39) for relativistic matter, with , is
| (2.130) |
But for ultra-relativistic gases, we know that the energy density is given by (2.131), have
| (2.131) |
where is the effective number of relativistic degrees of freedom (2.127). Differentiating this with respect to time, and assuming that is constant, we have
where the second expression comes from (2.130). This is just re-deriving the fact that . However, now we have use the Friedmann equation to determine the Hubble parameter in the radiation dominated universe,
This leaves us with a straightforward differential equation for the temperature,
| (2.132) |
We choose to set the integration constant to zero. This means that the temperature diverges as we approach the Big Bang singularity at . All times will be measured from this singularity.
To turn this into something physical, we need to make sense of the morass of fundamental constants in . The presence of Newton’s constant is associated with a very high energy scale known as the Planck mass with the corresponding Planck energy,
Meanwhile, the value of Planck’s constant is
These combine to give
Putting these numbers into (2.132) gives is an expression that tells us the temperature at a given time ,
| (2.133) |
Ignoring the constants of order 1, we say that the universe was at a temperature of approximately 1 second after the Big Bang.
As an aside: most textbooks derive the relationship (2.133) by assuming conservation of entropy (which, it turns out, ensures that is constant). The derivation given above is entirely equivalent to this.
To finish, we need to get a handle on the effective number of relativistic degrees of freedom . In the very early universe many particles were relativistic and is bigger. As the universe cools, it goes through a number of stages where drops discontinuously as the heavier particle become non-relativistic.
For example, when temperatures are around , the relativistic species are the photon (with ), three neutrinos and their anti-neutrinos (each with ) and the electron and positron (each with ). The effective number of relativistic species is then
| (2.134) |
As we go back in time, more and more species contribute. By the time we get to , all the particles of the Standard Model are relativistic and contribute .
In contrast, as we move forward in time, decreases. Considering only the masses of Standard Model particles, one might naively think that, as electrons and positrons annihilate and become non-relativistic, we’re left only with photons, neutrinos and anti-neutrinos. This would give
Unfortunately, at this point one of many subtleties arises. It turns out that the neutrinos are very weakly interacting and have already decoupled from thermal equilibrium by the time electrons and protons annihilate. When the annihilation finally happens, the bath of photons is heated while the neutrinos are unaffected. We can still use the formula (2.131), but we need an amended definition of to include the fact that neutrinos and electrons are both relativistic, but sitting at different temperatures. For now, I will simply give the answer:
| (2.135) |
I will very briefly explain where this comes from in Section 2.5.4.
A Longish Aside on Neutrinos
Why do neutrinos only contribute 1 degree of freedom to (2.134) while the electron has 2? After all, they are both spin- particles. To explain this, we need to get a little dirty with some particle physics.
First, for many decades we thought that neutrinos are massless. In this case, the right characterisation is not spin, but something called helicity. Massless particles necessarily travel at the speed of light; their spin is aligned with their direction of travel. If the spin points in the same direction as the momentum, then it is said to be right-handed; if it points in the opposite direction then it is said to be left-handed. It is a fact that we’ve only ever observed neutrinos with left-handed helicity and it was long believed that the right-handed neutrinos simply do not exist. Similarly, we’ve only observed anti-neutrinos with right-handed helicity; there appear to be no left-handed anti-neutrinos. If this were true, we would indeed get the count that we saw above.
However, we now know that neutrinos do, in fact, have a very small mass. Here is where things get a little complicated. Roughly speaking, there are two different kinds of masses that neutrinos could have: they are called the Majorana mass and the Dirac mass. Unfortunatey, we don’t yet know which of these masses (or combination of masses) the neutrino actually has, although we very much hope to find out in the near future.
The Majorana mass is the simplest to understand. In this scenario, the neutrino is its own anti-particle. If the neutrino has a Majorana mass then what we think of as the right-handed anti-neutrino is really the same thing as the right-handed neutrino. In this case, the counting goes through in the same way, but we drape different words around the numbers: instead of getting from each neutrino + anti-neutrino, we instead get spin states for each neutrino, and no separate contribution from the anti-neutrino.
Alternatively, the neutrino may have a Dirac mass. In this case, it looks much more similar to the electron, and the correct counting is 2 spin states for each neutrino, and another 2 for each anti-neutrino. Here is where things get interesting because, as we will explain in Section 2.5.3, we know from Big Bang nucleosynthesis that the count (2.134) of was correct a few minutes after the Big Bang. For this reason, it must be the case that 2 of the 4 degrees of freedom interact very weakly with the thermal bath, and drop out of equilibrium in the very early universe. Their energy must then be diluted relative to everything else, so that it’s negligible by the time we get to nucleosynthesis. (For example, there are various phase transitions in the early universe that could dump significant amounts of energy into half of the neutrino degrees of freedom, leaving the other half unaffected.)
2.5.2 The Thermal History of our Universe
The essence of the hot Big Bang theory is simply to take the temperature scaling and push it as far back as we can, telling the story of what happens along the way.
As we go further back in time, more matter joins the fray. For some species of particles, this is because the interaction rate is sufficiently large at early times that it couples to the thermal bath. For example, there was a time when both neutrinos and (we think) dark matter were in equilibrium with the thermal bath, before both underwent freeze out.
For other species of particle, the temperatures are so great (roughly ) that particle-anti-particle pairs can emerge from the vacuum. For example, for the first six seconds after the Big Bang, both electrons and positrons filled the fireball in almost equal numbers.
The goal of the Big Bang theory is to combine knowledge of particle physics with our understanding of thermal physics to paint an accurate picture for what happened at various stages of the fireball. A summary of some of the key events in the early history of the universe is given in the following table. In the remainder of this section, we will tell some of these stories.
| What | When | When | When |
| Inflation | s ? | ? | ? |
| Baryogenesis | ? | ? | ? |
| Electroweak phase transition | s | K | |
| QCD phase transition | s | K | |
| Dark Matter Freeze-Out | ? | ? | ? |
| Neutrino Decoupling | 1 second | K | |
| Annihilation | 6 second | K | |
| Nucleosynthesis | 3 minutes | K | |
| Matter-Radiation Equality | 50,000 years | 3400 | 8700 K |
| Recombination | years | 1300 | 3600 K |
| Last Scattering | 350,000 years | 1100 | 3100 K |
| Matter- Equality | years | 0.4 | 3.8 K |
| Today | years | 0 | 2.7 K |
2.5.3 Nucleosynthesis
One of the best understood processes in the Big Bang fireball is the formation of deuterium, helium and heavier nuclei from the thermal bath of protons and neutrons. This is known as Big Bang nucleosynthesis. It is a wonderfully delicate calculation, that involves input from many different parts of physics. The agreement with observation could fail in a myriad of ways, yet the end result agrees perfectly with the observed abundance of light elements. This is one of the great triumphs of the Big Bang theory.
Full calculations of nucleosynthesis are challenging. Here we simply offer a crude sketch of the formation of deuterium and helium nuclei.
Neutrons and Protons
Our story starts at early times, second, when the temperature reached MeV. The mass of the electron is
so at this time the thermal bath contains many relativistic electron-positron pairs. These are in equilibrium with photons and neutrinos, both of which are relativistic, together with non-relativistic protons and neutrons. Equilibrium is maintained through interactions mediated by the weak nuclear force
These reactions arise from the same kind of process as beta decay, .
The chemical potentials for electrons and neutrinos are vanishingly small. Chemical equilibrium then requires , and the ratio of neutron to proton densities can be calculated using the equation (2.112) for a non-relativistic gas,
The proton and neutron have a very small mass difference,
This mass difference can be neglected in the prefactor, but is crucial in the exponent. This gives the ratio of protons to neutrons while equilibrium is maintained
For , there are more or less equal numbers of protons and neutrons. But as the temperature falls, so too does the number of neutrons.
However, the exponential decay in neutron number does not continue indefinitely. At some point, the weak interaction rate will drop to , at which point the neutrons freeze out, and their number then remains constant. (Actually, this last point isn’t quite true as we will see below but let’s run with it for now!)
The interaction rate can be written as . where is the cross-section. At this point, I need to pull some facts about the weak force out of the hat. The cross-section varies as temperature as with a constant that characterises the strength of the weak force. Meanwhile, the number density scales as . This means that .
The Hubble parameter scales as in the radiation dominated epoch. So we do indeed expect to find at early times and at later times. It turns out that neutrons decouple at the temperature
Putting this into (2.133), and using , we find that neutrons decouple around
after the Big Bang.
At freeze out, we are then left with a neutron-to-proton ratio of
In fact, this isn’t the end of the story. Left alone, neutrons are unstable to beta decay with a half life of a little over 10 minutes. This means that, after freeze out, the number density of neutrons decays as
| (2.136) |
where second. If we want to do something with those neutrons (like use them to form heavier nuclei) then we need to hurry up: the clock is ticking.
Deuterium
Ultimately, we want to make elements heavier than hydrogen. But these heavier nuclei contain more than two nucleons. For example, the lightest is which contains two protons and a neutron. But the chance of three particles colliding at the same time to form such a nuclei is way too small. Instead, we must take baby steps, building up by colliding two particles at a time.
The first such step is, it turns out, the most difficult. This is the step to deuterium, or heavy hydrogen, consisting of a bound state of a proton and neutron that forms through the reaction
The binding energy is
Both the proton and neutron have spin , and so have . In deuterium, the spins are aligned to form a spin 1 particle, with . The fraction of deuterium is then determined by the Saha equation (2.117), using the same arguments that we saw in recombination
Approximating in the pre-factor, the ratio of deuterium to protons can be written as
We calculated the time-dependent neutron density in (2.136). We will need this time-dependent expression soon, but for now it’s sufficient to get a ballpark figure and, in this vein, we will simply approximate the number of neutrons as
The baryon-to-photon ratio has not had the opportunity to significantly change between nucleosynthesis and the present day, so we have . (The last time it changed was when electrons and positrons annihilated, with .) Using the expression from (2.103) for the number of photons, we then have
| (2.137) |
We see that we only get an appreciable number of deuterium atoms when the temperature drops to a suitably small value. This delay in deuterium formation is mostly due to the large number of photons as seen in the factor . These same photons are responsible for the delay in hydrogen formation 300,000 years later: in both cases, any putative bound state is quickly broken apart as it is bombarded by high-energy photons at the tail end of the blackbody distribution.
Solving (2.137), we find that only when , or
Importantly, this is after the neutrinos have decoupled. Using (2.133), again with , we find that deuterium begins to form at
This is around six minutes after the Big Bang. Fortunately (for all of us), six minutes is not yet the 10.5 minutes that it takes neutrons to decay. But it’s getting tight. Had the details been different so that, say, it took 12 minutes rather than 6 for deuterium to form, then we would not be around today to tell the tale. Building a universe is, it turns out, a delicate business.
Helium and Heavier Nuclei
Heavier nuclei have significantly larger binding energies. For example, the binding energy for is 7.7 MeV, while for it is 28 MeV. In perfect thermal equilibrium, these would be present in much larger abundancies. However, the densities are too low, and time too short, for these nuclei to form in reactions involving three of more nucleons coming together. Instead, they can only form in any significant levels after deuterium has formed. And, as we saw above, this takes some time. This is known as the deuterium bottleneck.
Once deuterium is present, however, there is no obstacle to forming helium. This happens almost instantaneously through
Because the binding energy is so much higher, all remaining neutrons rapidly bind into nuclei. At this point, we use the time-dependent form for the neutron density (2.136) which tells us that the number of remaining neutrons at this time is
Since each atom contains two neutrons, the ratio of helium to hydrogen is given by
A helium atom is four times heavier than a hydrogen atom, which means that roughly 25% of the baryonic mass sits in helium, with the rest in hydrogen. This is close to the observed abundance.
Only trace amounts of heavier elements are created during Big Bang nucleosynthesis. For each proton, approximately deuterium nuclei and nuclei survive. Astrophysical calculations show that this a million times greater than the amount that can be created in stars. There are even smaller amounts of and , all in good agreement with observation.
The time dependence of the abundance of various elements in shown88 8 This figure is taken from Burles, Nollett and Turner, Big-Bang Nucleosynthesis: Linking Inner Space and Outer Space”, astro-ph/99033. in Figure 31. You can see the red neutron curve start to drop off as the neutrons decay, and the abundance of the other elements rising as finally the deuterium bottleneck is overcome.
Any heavier elements arise only much later in the evolution of the universe when they are forged in stars. Because of this, cosmologists have developed their own version of the periodic table, shown in the Figure 32. It is, in many ways, a significant improvement over the one adopted by atomic and condensed matter physicists.
Dependence on Cosmological Parameters
The agreement between the calculated and observed abundancies provides strong support for the seemingly outlandish idea that we know what we’re talking about when the universe was only a few minutes old. The results depend in detail on a number of specific facts from both particle physics and nuclear physics.
One input into the calculation is particularly striking. The time at which deuterium finally forms is determined by the equation (2.133) which, in turn, depends on the number of relativistic species . If there are more relativistic species in thermal equilibrium with the heat bath then the deuterium bottleneck is overcome sooner, resulting in a larger fraction of helium. Yet, the contribution from the light Standard Model degrees of freedom (i.e. the photon and neutrinos) gives excellent agreement with observation.
This puts strong constraints on the role of dark matter in the early universe. Given its current prominence, we might naively have thought that the relativistic energy density in the early universe would receive a significant contribution from dark matter. The success of Big Bang nucleosynthesis tells us that this is not the case. Either there are no light particles in the dark sector (so the dark sector is dark even if you live there) or hot dark particles fell out of equilibrium long before nucleosynthesis took place and so sit at a much lower temperature when the all action is happening.
2.5.4 Further Topics
There are many more stories to tell about the early universe. These lie beyond the scope of this course, but here is a taster. Going back in time, we have…
Electron-Positron Annihilation
Prior to nucleosynthesis, the fireball included both electrons and positrons. At around these annihilate, injecting energy into the thermal bath of photons and slightly raising their temperature.
We can give an estimate for this. Prior to annihilation, the photons and electron-positron pairs were in equilibrium, giving
Afterwards, there are only photons with
So far, we haven’t looked closely at what happens when changes. This is because we need an important concept that we haven’t yet introduced: entropy. This is discussed in detail in the lectures on Statistical Physics where we show that the entropy of an ultra-relativistic gas is proportional to .
The annihilation of electron-positron pairs is an adiabatic process, which means that entropy is conserved. Since decreases by a factor of , this means that increases by . Or
There is one last twist to the story. The electrons and positrons do not all annihilate. There must be a very slight excess of electrons that are left over at the end. This, of course, is the stuff we’re made of.
Before annihilation, the number of electron-positron pairs was the same order of magnitude as the number of photons, and these have persisted to the present day. Meanwhile, electric neutrality of the universe ensures that the number of left over electrons is comparable to the number of baryons currently in the universe. This means that the slight excess of electrons in the early universe must be roughly equal to the famous ratio of baryons to photons in the present day. In other words, in the early universe there was one extra electron for every billion electron-positron pairs. Understanding the origin of this imbalance is the goal of baryogenesis and is briefly described below.
Neutrino Decoupling
Neutrinos are very weakly interacting. They decouple from the thermal bath at temperatures of . Neutrinos have masses between an meV and an eV (the exact masses are not well known) so they are very relativistic when they decouple. Like the photons after recombination, neutrinos preserve their relativistic distribution even after they decouple.
However, in contrast to the photons, neutrinos do not get the energy boost from electron-positron annihilation. This means that their temperature after this event lags behind the photon temperature, with
This relation persists to the present day. It is expected that there is a cosmic neutrino background filling the universe, with a temperature . This has not yet been observed although there is an experiment, currently in the design phase, which aims to detect it.
When we have relativistic species that sit at different temperatures, we need to revisit our formula for the effective number of degrees of freedom . We can continue to write the total energy density as
if we now define to be the sum over all relativistic species, whether or not they are in equilibrium,
where is the temperature of each species. In particular, after annihilation, when nucleosynthesis occurs, the relativistic species are photons and electrons with
This is the value quoted in (2.135) and used when discussing nucleosynthesis.
QCD Phase Transition
At a temperature of , protons and neutrons melt. They disassociate into a soup of quarks and gluons, known as the quark-gluon plasma. This state of matter has been created at particle accelerators here on Earth, freeing the quarks from their nucleon prison for the first time in 13.8 billion years.
Electroweak Phase Transition
In the Standard Model, fundamental particles such as the electron and quarks get their mass from the Higgs mechanism. Above , this mechanism ceases to work. At this point all particles in the Standard Model are massless and in thermal equilibrium.
Dark Matter Freeze Out
Clearly there are many things we don’t know about dark matter. We don’t, for example, know if it has any interactions with the stuff we’re made of. We can, however, make some assumptions and see where it leads us.
One of the most popular candidates for dark matter is a stable, massive particle that interacts only weakly with itself and with the Standard Model. These are known as weakly interacting massive particles, or WIMPs. Nearly all theories that go beyond the Standard Model predict such objects.
If the particle interacts even weakly with the Standard Model then there will be a time when dark matter is in equilibrium with the thermal bath. As the temperature lowers, the dark matter will freeze out. With very little input — just the mass and cross-section of the dark matter — we can then compute the expected abundance of dark matter seen today.
Here something nice happens. If we take the mass to be around , which is the energies probed by the LHC, and the cross-section to be , which is the strength of the weak nuclear force, then we do indeed find the observed abundance of dark matter. With an overblown rhetorical flourish, this coincidence is known as the WIMP miracle. It was one of the reasons for optimism that it might be possible to create dark matter at the LHC. Needless to say, this was not borne out. Furthermore, a slew of impressive experiments, designed to directly detect passing dark matter, have so-far, offered only null results. While WIMPs remain a possible candidate for dark matter, there is no compelling observation beyond the coincidence above to suggest they are intimately tied to the weak force at the 100 GeV scale.
Baryogenesis
The universe contains lots of matter but very little anti-matter. How did this asymmetry come to be?
One possibility is that it is an initial condition on the universe. Another is that the universe started with equal amounts of matter and anti-matter, but somehow a small dynamical shift took place that preferred one over the other. This latter process is known as baryogenesis.
We don’t have an established theory of baryogenesis; whatever caused it must lie beyond the Standard Model. Nonetheless, there are criteria, known as the Sakharov conditions that must be obeyed for baryogenesis to occur:
-
•
The first criterion is the most obvious: baryon number cannot be a conserved quantity. Here “baryon number” refers to baryons minus anti-baryons. In a symmetric universe, this starts off as zero. We want it to end up non-zero.
In the Standard Model, baryon number is conserved. (In fact, strictly speaking is conserved where is baryon number and is lepton number, but this is a story for another day.) But it is straightforward to cook up interactions at higher energy scales which violate baryon number.
-
•
There is a symmetry known as CP which, roughly speaking, says that particles and anti-particles behave the same. This too must be violated for baryogenesis to occur, since particles should be favoured over anti-particles.
In fact, CP is violated in the Standard Model. It’s not clear if this is sufficient, or if further CP violation is needed in the interaction beyond the Standard Model.
-
•
The final criterion is the least obvious: the early universe must deviate from thermal equilibrium. This is needed so that the interactions in one direction differ from the interactions running in reverse.
A deviation from thermal equilibrium occurs when the universe undergoes a first order phase transition. (You can read more about phase transitions in the lectures on Statistical Physics and Statistical Field Theory.) The electroweak phase transition appears to be a fairly smooth crossover, which is not violent enough to do the job. For baryogenesis to occur, we most likely need a different phase transition early in the universe.
There are many models of baryogenesis, but currently no smoking gun experiment or observation to determine which, if any, is correct.