The Partonic Nature of Instantons
This page contains mathematica notebooks to accompany the paper "The Partonic Nature of Instantons", arXiv:0905.2267 [hep-th] by Ben Collie and David Tong.
![[Squashing]](research/cp1a.jpeg)
Squashing CP1
This notebook computes the energy density of a single BPS lump with target
space CP1. As the squashing parameter is varied, the
lump decomposes into two partons.
The notebook can be downloaded here.
Notes: The equations in this notebook are derived from the Bogomolnyi equation (2.9) in the paper, along with the equation (2.5) for H and equations (2.6) and (2.10) for σ. If we set m=1 then we find:
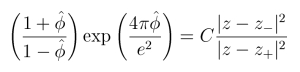
|
The constant C on the RHS gives the limit as z → ∞ of the LHS. In this notebook, C is set to 1. The quantity Ω in the notebook is proportional to the topological charge density, and is given by:
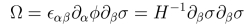
|
![[Changing Vacuum]](research/cp1b.jpeg)
Changing the Vacuum
This notebook studies the CP1 lump as the vacuum
is vared and the parton distribution function changes.
The notebook can be downloaded here.
Notes: The equations in this notebook are essentially the same as in the previous one, but now the constant C is allowed to depend on the vacuum value of phi-hat.
![[Squashing]](research/cp2a.jpeg)
Squashing CP2
This notebook computes the energy density of a single BPS lump with target
space CP2. As the squashing parameter is varied, the
lump decomposes into three partons.
The notebook can be downloaded here.
Notes:The equations in this notebook are derived from the Bogomolynyi equation at the start of section 3.2 of the paper, together with the equations (3.8) for H-hat and (3.9) for σ-hat. We find:
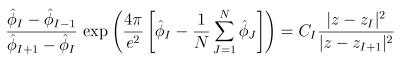
|
where C_I is the limit of the LHS as z → ∞. This equation is rewritten in terms of new variables
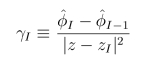
|
which are everywhere regular. We assume that phihat1 = - phihat2 = - m/2 in the vacuum. The quantity Ω that is proportional to the topological charge density is then defined by
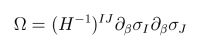
|
![[Moving]](research/cp2b.jpg)
Moving the Partons
This notebook shows how the three partons inside the CP2
lump move as the "orientation modes" are varied, with the scale size kept fixed.
The notebook can be downloaded here.
Notes: The equations in this notebook are essentially the same as in the previous one, except now the parton positions are given parametrically in terms of three parameters. The first is the soliton scale size r:
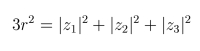
|
The other two are internal orientation parameters:
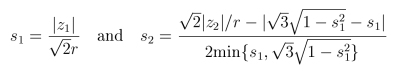
|
![[Toric]](research/toric.jpg)
The Toric Image in CP2
This interactive notebook computes the image of the CP1
submanifold of the lump inside CP2 in toric
coordinates.
The notebook can be downloaded here.
Notes: We choose co-ordinates on the plane so that the three partons sit on a circle centered at the origin. We then construct phihatI for each point within this circle using equation (3.9) from the paper.
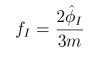
|