Theoretical physics is the effort to create mathematical models that describe phenomena in nature and to make predictions with these models that can be tested through experiment and observation. The standard model (SM) of particle physics and Einstein's theory of general relativity (GR) are the two main pillars of modern day theoretical physics that provide us with a magnificent framework to understand much of what we see in the universe. From the microscopic regime of elementary particles colliding near the speed of light at the Large Hadron Collider at CERN to the gravitational wave symphony of black holes and the cosmological evolution of the observable universe itself, the model gives us highly accurate predictions that have been verified in numerous experiments and observation programs. Background and Motivation
And yet, there are gaps in this exquisite picture and indications that something is not quite right or, at least, incomplete about our understanding of the world of physics. None of these observations are in direct conflict with the SM+GR model, but they require us to add increasingly enigmatic ingredients to the model. For example, galactic rotation curves, strong gravitational lensing and precision measurements of the cosmic microwave background cannot be explained in terms of the visible matter. Either we accept the existence of an unknown form of dark matter, whose form we can, at present, not satisfactorily explain within the standard model of particle physics, or we are prepared to modify the laws of gravity beyond Einstein's relativity. Likewise, the accelerated expansion of the universe calls for an even more exotic substance dubbed dark energy or, equivalently, the introduction of a cosmological constant (the very constant Einstein introduced himself but later discarded as "the biggest blunder of his life"). By now, the cosmological constant is regarded as a perfectly legitimate ingredient in Einstein's theory, but its value is problematic. The value it needs to have to explain observations in cosmology is about 60 orders of magnitude smaller than expected from the zero-point energy predicted by the standard model of particle physics. Further chinks in the armor of the SM+GR model include the hierarchy problem of physics, i.e. the extraordinary weakness of gravity relative to the other forces of nature, and the seeming irreconcilability of general relativity with quantum theory. These questions are deeply related to the nature of gravity and the quest for answers forms the core of our RISE project "Strong Gravity and High-Energy Physics".
When Isaac Newton presented his theory of the gravitational interaction in the 1680s, he had developed the first ever comprehensive scientific theory of a fundamental physical interaction in mathematical terms. The power of the Newtonian Theory of Gravity is so enormous that it has even been used in many applications in the 20th and 21st century including, as a most dramatic and successful example, the Apollo moon landing in 1969. It may seem surprising therefore, that gravitation remains to this day the most enigmatic of the four fundamental forces of nature. Over the course of the 20th century, the other three forces (electromagnetism, the strong and the weak nuclear force) have been combined into a joint framework that has passed a wealth of experimental tests and underlies much of modern technology -- this is the standard model of particle physics. However, all efforts to bring Gravity into this family have not yet succeeded. It is for this reason that we speak of the SM+GR model rather than one single theory encompassing all four interactions. And indeed, there is something special about gravitation that has already been noticed as early as the turn of the fifth century by Philoponus and later on by Galileo, Newton himself and eventually Einstein.
All forces in nature can be regarded as the effect of a "charge", best known to us in the case of the electric charge that drives our computers, televisions, chemistry and our own bodies. Also, all objects have inertia, the higher their inertia, the stronger a force is required to change the object's state of motion. This inertia is a characteristic of a body that has nothing to do with its electric charge nor with its characteristic charge for the weak and strong nuclear forces. But, and that's the critical point, the inertia happens to be exactly the same as the gravitational charge: the inertial mass of any body is exactly the same as its gravitational mass. This fact underlies the well-known feature that all bodies fall the same way, as demonstrated by astronauts on the moon when they dropped a feather and a hammer. This special feature lead Einstein to the revolutionary (but now ubiquitously accepted) idea that gravity is not really a force at all and not even a feature of any particular body but is a quality of the fabric of space and time the bodies move in -- this is called the equivalence principle.
But even with Einstein's theory, we are left with the questions listed above. In our search for answers, we can now employ a new channel to observing the universe that only became available about two years ago: Gravitational waves. On February 11, 2016, the LIGO-Virgo Scientific Collaboration replaced US Presidential hopefuls in the newspaper headlines by announcing the first detection of gravitational waves which also provided the first direct observation of a black hole.

Snapshot of a numerical simulations of 2 black holes with parameters similar to the GW150914 event detected by LIGO during the inspiral phase. The gravitational waves are propagating outwards from the black-hole binary. (Courtesy of Markus Kunesch)
More specifically, the goals of our project can be summarized as follows. (1) What can we learn about the enigmatic dark matter from observing black holes? There is a wide variety of phenomena, such as runaway resonance effects in the interaction between dark-matter candidate fields and black holes, that may yield characteristic signatures in gravitational and electromagnetic radiation. (2) Are black holes really the specific class of objects described by general relativity or is there yet another twist to them? Gravitational waves are our best hope of testing this, and our computations search for differences between the radiation signal emitted by black holes and that from more exotic alternatives. (3) Can we directly observe the spacetime distortion created by black holes? This may be possible in the form of the shadow cast by a black hole and the obscuration or lensing of luminous objects located behind it. (4) How can we test whether Einstein's theory is also correct in the regime of extremely strong gravity? Do we need to generalize the theory? We calculate "smoking gun" phenomena that alternative theories of gravity predict for black holes, neutron stars or other astrophysical objects. (5) Our world has four dimensions, one time and three space directions. Or does it? There are suggestions that there may be extra dimensions inaccessible to anything but gravity. This would explain why gravitation is so weak in laboratory experiments. And it would predict potentially observable features in particle collisions at extremely high energy. Our simulations of black holes in higher dimensions will contribute to our understanding of what we would see if extra dimensions exist. Or maybe there is something special about four dimensions and universes with more dimensions would not allow for the evolution of intelligent beings capable of asking such questions.
From a practically minded viewpoint, one might wonder, of course, why we should pursue questions like this when immediate technical benefit is not obvious. All our historical experience, however, thunders a warning against such a narrow viewpoint: Fundamental research may at times be glacially slow in providing practical benefits, but in the end it always does and does so with the overwhelming power of a glacier. Quantum mechanics, for instance, is probably the most bizarre (and yet correct) theory ever designed by humans. But it now forms the foundation for all modern electronics, from rocket science to the smart phone. Number theory, arguably the purest form of academic exercise, was pursued as early as about 3000 years ago in antique Greece. All of modern encryption, however, would not exist without it. Secure internet trading and banking rely on number theory! General relativity itself found its way into a multi-billion Euro business: GPS type navigation would be of negligible practical use without the corrections of Einstein's theory. Furthermore, the fascination with astrophysics and the fundamental building blocks of our world has attracted over centuries young researchers, taking over and forming the next generation of leaders in science and technology. Carrying across this fascination to the public and to the young physics stars of tomorrow is a fundamental (and most rewarding) task and forms a second major goal of our project, besides our immediate research studies.
Introduction
The situation of modern physics can be summarized as follows. We have an exquisite model, but we also have considerable observational evidence pointing to physics beyond this SM+GR model. Before we go into more details on how we explore "beyond SM+GR" physics in our project, it is important to realize that such a situation is not new; we have been in it before. And the parallels with our current status are so striking that we should take a moment to see what lessons history may teach us.
Based on Newton's laws of motion and gravity, Alexis Bouvard calculated in 1821 tables predicting the future evolution of the orbit of Uranus around the sun and where in the sky we would find it. Observations of the actual positions of Uranus, however, were soon found to deviate from these predictions. Having eliminated the possibility of factual errors in his calculations, Bouvard and others started speculating that there must exist another celestial body that perturbs Uranus' orbit away from the predictions. In modern language, we would call this a "dark matter hypothesis", the proposition that there exist previously unknown material exercising a gravitational effect in accordance with the present theory of gravity, but not having been taken into account since it had not yet been seen by other means. Over the ensuing year, Adams, Le Verrier and others calculated from the deviations of Uranus' motion where this new planet should be. In 1846, a new planet -- Neptune -- was observed within one degree of this position in the sky.
Around that time, Le Verrier also started studying the motion of the planet Mercury. By 1859, he had accumulated enough evidence to report that Mercury's motion -- to be precise, the precession of Mercury's perihelion from one orbit to the next -- could not be explained in terms of the gravitational effect of the sun and the other known planets according to Newtonian gravity. Spurred on by the successful "dark matter" model that lead to the discovery of Neptune, astronomers proposed the existence of a further planet located between the sun and Mercury. It was appropriately named Vulcan after the Roman god of fire; but Vulcan was never found. Instead, the observed discrepancy was ultimately explained by Einstein who derived the correct value for Mercury's perihelion precession from his new theory of general relativity. In modern day language, we would call his theory a "modified" or "alternative" theory of gravity. It is important to note that this does not invalidate the Newtonian theory. Newtonian theory remains highly accurate in the regime of comparatively weak gravity as we experience, for instance, on planet Earth. But for strong fields, Newtonian gravity had to be extended to a more comprehensive theory. In the limit of weak fields, Einstein's general relativity indeed reproduces with high precision the predictions of Newtonian gravity, but for stronger fields, it makes different predictions that agree better with observations.
It is in this sense, that scientists now search for modifications of general relativity. These theories will agree with Einstein's relativity for many physical systems, but may show new features in the -- as yet poorly tested -- regime of extreme spacetime curvature. A second lesson we learn from this historic experience is to keep our minds open. Dark matter and modified gravity may both provide answers to our puzzles. Both avenues have had their success and failure in the past. In our project, we therefore explore both possibilities; in part A, we largely concentrate on dark matter scenarios while part B is largely concerned with possible modifications of gravity.
Part A: Dark Matter
The particles of nature can be categorized into two families called bosons and fermions. Fermions include the proton and electron and, roughly speaking, make up most of what we see as ordinary matter while the most familiar member of the boson family is the photon; more generally, bosons comprise particles that mediate forces. The most fundamental difference between the two is that fermions obey the Pauli principle (no two fermions are allowed to be in the same state) which leads to a "degeneracy pressure" which supports white dwarfs and neutron stars. The currently most promising dark matter candidates are boson fields and are thus not subject to Pauli's exclusion principle. We have modeled a wide range compact objects surrounded by or composed of bosonic fields and summarize our results as follows.
It has been believed that bosonic dark matter accumulating around compact stars, not being supported by Fermi degeneracy pressure, would trigger the formation of black holes, resulting in the destruction of the star. One of our main findings is that this is not the case; rather, the bosonic matter clusters near the center of the star but oscillates with a characteristic frequency instead of inducing gravitational collapse.
A particularly intriguing type of interaction between a bosonic field surrounding a rapidly rotating black hole is a resonant effect called "superradiance". This effect is akin to the Penrose process whereby rotational energy can be extracted from a spinning black hole. The Penrose effect underlies the speculative idea that civilizations on a planet orbiting a black hole rather than a star like the sun, might well be able to gain energy from their central object with as much efficiency as we get it from the sun. For our purposes, the most important effect of superradiance is the amplification of the boson field and the corresponding reduction in the black hole's rotation. This effect may give characteristic gravitational signatures in the form of "floating orbits" in binaries, where the energy loss in gravitational radiation is balanced by the energy extraction from the individual black hole's spin.
We have identified a wide range of additional observational signatures of superradiance in the form of voids in the spin-mass diagram of black hole populations (highly spinning black holes would be exceptionally rare as they have lost rotation energy through superradiance). Present and future gravitational wave detectors could either identify or rule out the presence of boson fields over a wide range of the boson mass parameter.
Boson fields can also exist in the form of compact, self-gravitating "boson stars" with a density comparable to that of neutron stars. This raises the question whether gravitational wave detectors might see the inspiral and merger phase of two such boson stars and distinguish it from the inspiral and merger of neutron stars or black holes. By numerically modeling boson star binaries, we have identified a characteristic oscillation pattern in the post-merger phase of the gravitational wave signal that distinguishes boson stars from the more traditional compact binaries.
A critical question concerning black holes surrounded by boson fields is their stability. Long-term stability is a key criterion to consider an object as a viable observational candidate in astrophysics. For instance, if a black hole surrounded by a boson field rapidly absorbs the field, it will have changed into a normal black hole well before we have had a chance to observe it.
In work done prior to this project, some of us have found exact, stationary solutions describing a black hole with a complex boson field, either a scalar (spin 0) or vector (spin 1) field. We have now shown that these configurations may indeed form the end point of an initially dynamic configuration consisting of a black hole surrounded by an initially disordered vector field. We have furthermore numerically studied an analogous situation where the superradiance is not sourced by the black hole rotation but by its electric charge. Our results indicate that these "hairy black holes" may indeed be sufficiently long lived to play a potentially important role in astrophysics. We will perform more numerical studies to strengthen our evidence in this direction.
Gravitational waves are likely our most promising channel to identify these signatures of as yet unobserved matter in the universe. But they are not the only possibility. A class of astrophysical X-ray sources is believed to consist of a black hole surrounded by ordinary matter that accretes onto the hole, heats up enormously in the process and emits X-rays before finally disappearing behind the black hole horizon. This X-ray flux sometimes exhibits quasi-periodic oscillations that can be measured. We have shown that the presence of a boson field around these accreting compact objects leads to a shift in the quasi periodic oscillation frequencies that may be identified in X-ray observations provided we see enough sources. With future missions such as the European LOFT space mission, we will be able to either see these signatures or, in case of a zero result, be able to set very stringent bounds on the amount of boson matter.
Through their strong gravity, black holes also cause a severe bending of light passing by. For instance, if light from a distant galaxy passes close by a black hole on its way to us, the light will be very strongly lensed and part of the galaxy image will be blocked by the intermittent hole. This is called the black hole shadow. We have identified that the image resulting from this strong lensing has a self similar structure containing an infinite number of ever smaller versions of the original image of the galaxy. The observation of this black hole lensing and of black hole shadows is a target for the Event Horizon Telescope and has the potential to distinguish run-of-the-mill black holes from their hairy counterparts or even more exotic "black-hole mimickers". Furthermore, the exact shape of the shadows depends on the underlying theory of gravity. In order to estimate the prospect of distinguishing between different theories of gravity in this way, we have computed the light bending in a specific extension of general relativity. The differences in the predicted shadows are, unfortunately, rather small, about 1% or less. This is a major challenge for present observatories, who are therefore likely to play a supportive, but not the dominant role in our search for modifications of general relativity.
In summary, we have identified a wide range of smoking gun effects through which dark matter candidates may reveal themselves or may be excluded in present and future gravitational wave and electromagnetic observations of astrophysical sources.
Part B: Modified Gravity
As we have seen in our discussion of the Neptune vs. Vulcan history the answer to the puzzles in current observations may also lie in the modification of the theory of gravity itself. The second part of our project is devoted to the identification of observational signatures to confirm or constrain such modifications. For this purpose, we have modeled a wide range of astrophysical processes involving neutron stars and black holes, looking for the signature of possible corrections to general relativity which modify the strong-field regime of gravity.
One particularly promising channel to detect such modifications is the multipolar structure of the gravitational wave signal. In general relativity, the signal is dominated by quadrupole radiation, since the inherently stronger monopole and dipole contributions inevitably vanish due to conservation of energy and momentum. In contrast, dipole and monopole radiation are possible in most alternative theories of gravity and, thus, constitute a smoking gun effect. We have explored this for several theories and calculated that the future European space based gravitational wave observatory LISA will be able to see dipole radiation from black hole binaries in several alternative theories and is thus capable of either confirming or constraining these theories.
A particularly strong effect in the so-called scalar tensor theory of gravity is a spontaneous scalarization of neutron stars -- an effect analogous to the spontaneous magnetization of ferro magnets. This effect has already been used to constrain scalar tensor theory through binary pulsar observations. These constraints, however, do not apply if the scalar field of the theory has a significant mass term. We have demonstrated that this wider class of "massive" scalar tensor theory results in a unique gravitational wave signal from supernova collapse, consisting of a long-lived (years or even centuries) almost monochromatic radiation pattern. A remarkable consequence is a gravitational wave afterglow of supernovae that could be seen by directing the groundbased LIGO and Virgo detectors at historic supernovae such as SN1987A or Kepler's supernova of 1604.
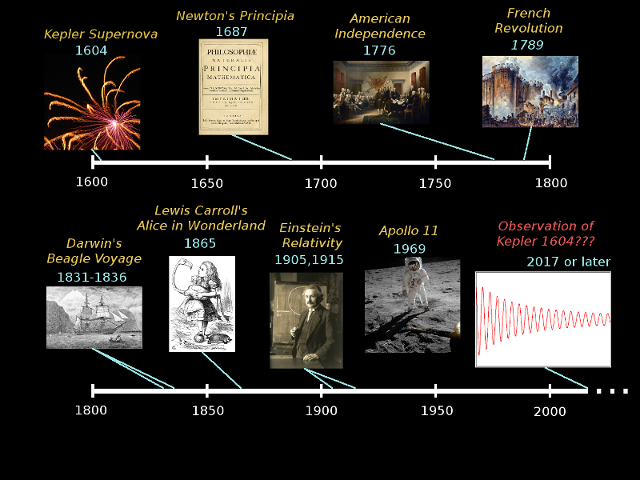
Timeline starting with the Kepler supernova observed in 1604 (upper left). Massive scalar tensor theory predicts a gravitational-wave afterglow from this event (bottom right) which we would still be able to detect more than 400 years after the first photons arrived from the explosion.
The quasi-periodic oscillations in the X-ray flux from accreting compact objects have already been noted as a promising tool to search for signatures of dark matter fields. We have developed analogous methods to use such observations to test general relativity against a generic class of so-called quadratic gravity theories.
The remnant black hole resulting from the merger of two compact objects is known to settle down through a ring-down (analogous to the way a bell rings down) with characteristic frequencies determined by the mass and spin of the black hole, but also on the underlying theory of gravity. We have calculated that future gravitational wave detectors, such as the Cosmic Explorer or LISA, will be able to test the true nature of black holes even at early times of the universe; this is particularly important, since we expect modifications of gravity away from general relativity (if they exist) to be stronger in the early universe than in our epoch.
A special type of modified gravity has been devised with particular regard to explaining the hierarchy problem of physics, i.e. the question why gravity is so many orders of magnitude weaker than the electromagnetic and nuclear forces. The idea consists in the existence of extra spatial dimensions that dilute gravity on length scales below a millimeter. On those scales, gravity is presently not constrained through measurements, but this regime may be probed in particle collisions at colliders such as the Large Hadron Collider. In consequence of extra dimensions, gravity would become the dominant force at collision energies well above a Terra electron volt (TeV) and the corresponding models are often referred to as TeV gravity. The experimental signature would be the formation of black holes in sufficiently energetic proton-proton collisions and the ensuing (highly characteristic) evaporation of these mini black holes through Hawking radiation. The high-energy collisions of two objects as compact as protons, however, results in a significant amount of energy radiated away in gravitational waves. This loss of energy would reduce the mass available for the formation of a black hole and the quantitative outcome of the experiment depends on this mass deficit as well as on other aspects of the collision dynamics. This information can only be obtained through numerical simulations which were still in their infancy at the start of our project.
The challenge then consists in modeling the collision of two point like particles over a wide range of velocities and spacetime dimensionality. We have developed, for this purpose, a comprehensive formalism that allows us to simulate collisions of black holes (black holes are the closest analog of point particles in fully non-linear gravity) in higher dimensions on supercomputers. We have furthermore constructed a method to extract from the numerical simulations with high precision the amount of energy radiated in gravitational waves. This method represents the generalization of the so-called Newman-Penrose scalars that have been used for decades in the simulations of astrophysical black holes in four dimensions.
Based on this framework, we have performed the first systematic exploration of the parameter space of black hole collisions in higher dimensional spacetimes. For low collision velocities and comparable masses of the two colliding holes, we have found the emission of gravitational waves to be strongly suppressed relative to the case of four spacetime dimensions. We have reconciled this surprising observation with previously performed perturbative calculations by taking into account a new characteristic length scale that arises in the gravitational interaction in higher dimensions.
As the next step, we have increased the collision velocity up to about 70% of the speed of light. Like in four dimensions, we see a dramatic increase in the radiated energy above velocities of about 20% of the speed of light, leading to a total loss of the order of 10% in the ultrarelativistic limit.
In a separate study, we have analyzed in detail the dynamics of single, rapidly rotating black holes in six spacetime dimensions with articular regard to testing Penrose's so-called cosmic censorship conjecture. Black hole solutions to Einstein's general relativity contain points where the spacetime curvature becomes infinite. Mathematically, such singularities are problematic, since they mark the breakdown of the predictability of the theory. It is a remarkable feature of Einstein's theory that these singularities are always hidden from an outside observer by an event horizon. According to Penrose's conjecture, this rescuing feature is a fundamental property of general relativity. In four dimensions, no generic counter examples have been found to date. In higher dimensions, however, the situation is different. We have demonstrated that rapidly spinning black holes in six dimensions generically lead to so-called naked singularities, i.e. singular points that are not hidden inside a horizon. This work does not constitute a proof, but it indicates that there may be something more special to the number of four spacetime dimensions, namely an inherent tendency to avoid highly pathological spacetime features.
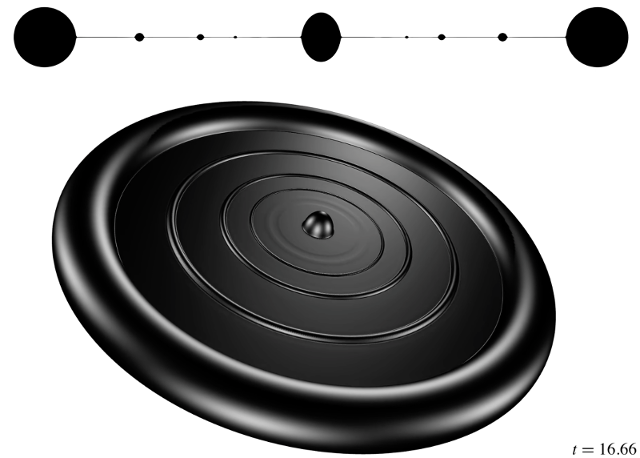
Late stages in the evolution of a rapidly rotating black hole in 6 spacetime dimensions (2 spatial dimensions are suppressed in the figure). The black hole evolves into a thin disk consisting of an increasing number of rings connected by ever thinner membranes (a cross section is shown at the top). These membranes reach zero width in finite time, signalling the formation of a "naked singularity". (Courtesy of Markus Kunesch)
In summary, we have identified a wealth of observable signatures that enable us to either identify modifications of Einstein's theory or to significantly constrain them through present and future observations or experiments.
Introduction
The state of the art in all areas of our project is reviewed in a set of three monographs co-authored by the members of this project and published shortly before the start of this project [arXiv:1409.0014, arXiv:1501.06570 and arXiv:1501.07274]. In the context of the RISE Action we have, already, gone significantly beyond the state of the art; all the work described above, as well as in more detail in the technical report, represents extension beyond the state of knowledge available at the start of this project. A summary of the most fundamental advances is given as follows.
Part A: Dark Matter
We demonstrated that rotational superradiance can be detected in labsize experiments, a proposal which has since been implemented: the first ever claim of detection of superradiance was recently reported.
We have performed the first fully nonlinear evolutions of superradiant instabilities in the context of charged black holes. These simulations are able to probe the nonlinear development of the mechanism as well as to probe its end state.
We have identified that the endpoints of these evolutions consist of a rotating black hole surrounded by boson fields synchronized with the rotation frequency of the hole.
We built the first example of a self-gravitating configuration of massive vector fields (called a Proca star), and we performed a comprehensive review of how these configurations are able to settle down and grow deep inside the core of compact stars.
We have shown that hairy black holes can form dynamically via two different channels: (i) by a hair-growth process around a "bald" black hole or (ii) by the decay of unstable solitons. In both cases the process is terminated by non-linear effects.
We have shown that unstable Proca stars can have three different fates: (i) total dispersion; (ii) collapse into a black hole; (iii) migration into a stable star.
We have argued that the growth of a bosonic cloud around an unstable black hole could be caused, in a realistic astrophysical environment, by the effective photon mass, which arises due to the galactic plasma. Potential astrophysical phenomenology was also discussed.
Part B: Modified Gravity
We have shown that joint observations of black-hole binary systems by LIGO and LISA will improve bounds on dipole emission from black-hole binaries by several orders of magnitude relative to current constraints.
We found that future ringdown detections with large signal-to-noise ratio, with ground-based gravitational wave detector such as aLIGO, and future observations by large-area X-ray detectors such as LOFT or eXTP, will be able to set significant constraints in the parameter space of quadratic gravity theories such as Einstein-Dilaton-Gauss-Bonnet gravity.
We assessed the possibility of doing "gravitational spectroscopy", i.e., to measure of multiple quasinormal mode frequencies from the remnant of a black hole mergers, using present and future gravitational-wave detector. Gravitational spectroscopy would be a powerful tool to test general relativity against possible modifications, and to test the black hole "no-hair" hypothesis.
We have derived solutions of Einstein-Aether theory describing slowly rotating black holes, studying the properties of these solutions, and discussing how they can be used to test general relativity against Einstein-Aether theory with astrophysical observations.
We have identified that stellar collapse in massive scalar tensor theory of gravity leads to long-lived, quasi-monochromatic signals spread out over years or centuries that may be seen by directing LIGO at historic supernovae.
Our extraction method in higher dimensions is the first fully consistent method that accounts for the entire amount of gravitational radiation.
We have performed the first systematic exploration of black-hole collisions in up to 10 spacetime dimensions. At low collision velocities, the emission of gravitational waves is significantly suppressed above about 7 dimensions. At larger collision velocities, above about 20% of the speed of light, however, the radiative efficiency increases strongly, reaching of the order of 10% of the total mass energy in the utrarelativistic limit.
We have demonstrated that rapidly rotating black holes in six spacetime dimensions lead to the formation of naked singularities -- pathological points in the spacetime not hidden inside an event horizon. This may set apart higher dimensional spacetimes from the four-dimensional case.
Future Outlook
In the second part of this project, we will continue our studies in accordance with the plan proposed for this project. The most urgent points to address are the following.
Perform more and longer numerical simulations of hairy black holes to obtain more quantitative estimates of their stability properties.
Perform binary simulations of hairy black holes and search for differences in the gravitational wave signal as compared with their "bald" counterparts.
Systematically explore the parameter space of the coalescence of binary boson-stars.
Extend our list of astrophysical observables of dark matter candidate fields around compact objects and characteristic signatures of alternative theories of gravity.
Compute black hole shadows in binary systems.
Extend our study for black-hole collisions in higher dimensions to the case of grazing collisions. Determine the scattering threshold and maximum efficiency in gravitational wave emission.