1 The Fundamentals of Statistical Mechanics
1.1 Introduction
Statistical mechanics is the art of turning the microscopic laws of physics into a description of Nature on a macroscopic scale.
Suppose you’ve got theoretical physics cracked. Suppose you know all the fundamental laws of Nature, the properties of the elementary particles and the forces at play between them. How can you turn this knowledge into an understanding of the world around us? More concretely, if I give you a box containing particles and tell you their mass, their charge, their interactions, and so on, what can you tell me about the stuff in the box?
There’s one strategy that definitely won’t work: writing down the Schrödinger equation for particles and solving it. That’s typically not possible for 23 particles, let alone . What’s more, even if you could find the wavefunction of the system, what would you do with it? The positions of individual particles are of little interest to anyone. We want answers to much more basic, almost childish, questions about the contents of the box. Is it wet? Is it hot? What colour is it? Is the box in danger of exploding? What happens if we squeeze it, pull it, heat it up? How can we begin to answer these kind of questions starting from the fundamental laws of physics?
The purpose of this course is to introduce the dictionary that allows you translate from the microscopic world where the laws of Nature are written to the everyday macroscopic world that we’re familiar with. This will allow us to begin to address very basic questions about how matter behaves.
We’ll see many examples. For centuries — from the 1600s to the 1900s — scientists were discovering “laws of physics” that govern different substances. There are many hundreds of these laws, mostly named after their discovers. Boyle’s law and Charles’s law relate pressure, volume and temperature of gases (they are usually combined into the ideal gas law); the Stefan-Boltzmann law tells you how much energy a hot object emits; Wien’s displacement law tells you the colour of that hot object; the Dulong-Petit law tells you how much energy it takes to heat up a lump of stuff; Curie’s law tells you how a magnet loses its magic if you put it over a flame; and so on and so on. Yet we now know that these laws aren’t fundamental. In some cases they follow simply from Newtonian mechanics and a dose of statistical thinking. In other cases, we need to throw quantum mechanics into the mix as well. But in all cases, we’re going to see how derive them from first principles.
A large part of this course will be devoted to figuring out the interesting things that happen when you throw particles together. One of the recurring themes will be that . More is different: there are key concepts that are not visible in the underlying laws of physics but emerge only when we consider a large collection of particles. One very simple example is temperature. This is not a fundamental concept: it doesn’t make sense to talk about the temperature of a single electron. But it would be impossible to talk about physics of the everyday world around us without mention of temperature. This illustrates the fact that the language needed to describe physics on one scale is very different from that needed on other scales. We’ll see several similar emergent quantities in this course, including the phenomenon of phase transitions where the smooth continuous laws of physics conspire to give abrupt, discontinuous changes in the structure of matter.
Historically, the techniques of statistical mechanics proved to be a crucial tool for understanding the deeper laws of physics. Not only is the development of the subject intimately tied with the first evidence for the existence of atoms, but quantum mechanics itself was discovered by applying statistical methods to decipher the spectrum of light emitted from hot objects. (We will study this derivation in Section 3). However, physics is not a finished subject. There are many important systems in Nature – from high temperature superconductors to black holes – which are not yet understood at a fundamental level. The information that we have about these systems concerns their macroscopic properties and our goal is to use these scant clues to deconstruct the underlying mechanisms at work. The tools that we will develop in this course will be crucial in this task.
1.2 The Microcanonical Ensemble
“Anyone who wants to analyze the properties of matter in a real problem might want to start by writing down the fundamental equations and then try to solve them mathematically. Although there are people who try to use such an approach, these people are the failures in this field…”
Richard Feynman, sugar coating it.
We’ll start by considering an isolated system with fixed energy, . For the purposes of the discussion we will describe our system using the language of quantum mechanics, although we should keep in mind that nearly everything applies equally well to classical systems.
In your first two courses on quantum mechanics you looked only at systems with a few degrees of freedom. These are defined by a Hamiltonian, , and the goal is usually to solve the time independent Schrödinger equation
In this course, we will still look at systems that are defined by a Hamiltonian, but now with a very large number of degrees of freedom, say . The energy eigenstates are very complicated objects since they contain information about what each of these particles is doing. They are called microstates.
In practice, it is often extremely difficult to write down the microstate describing all these particles. But, more importantly, it is usually totally uninteresting. The wavefunction for a macroscopic system very rarely captures the relevant physics because real macroscopic systems are not described by a single pure quantum state. They are in contact with an environment, constantly buffeted and jostled by outside influences. Each time the system is jogged slightly, it undergoes a small perturbation and there will be a probability that it transitions to another state. If the perturbation is very small, then the transitions will only happen to states of equal (or very nearly equal) energy. But with particles, there can be many many microstates all with the same energy . To understand the physics of these systems, we don’t need to know the intimate details of any one state. We need to know the crude details of all the states.
It would be impossibly tedious to keep track of the dynamics which leads to transitions between the different states. Instead we will resort to statistical methods. We will describe the system in terms of a probability distribution over the quantum states. In other words, the system is in a mixed state rather than a pure state. Since we have fixed the energy, there will only be a non-zero probability for states which have the specified energy . We will denote a basis of these states as and the probability that the systems sits in a given state as . Within this probability distribution, the expectation value of any operator is
Our immediate goal is to understand what probability distribution is appropriate for large systems.
Firstly, we will greatly restrict the kind of situations that we can talk about. We will only discuss systems that have been left alone for some time. This ensures that the energy and momentum in the system has been redistributed among the many particles and any memory of whatever special initial conditions the system started in has long been lost. Operationally, this means that the probability distribution is independent of time which ensures that the expectation values of the macroscopic observables are also time independent. In this case, we say that the system is in equilibrium. Note that just because the system is in equilibrium does not mean that all the components of the system have stopped moving; a glass of water left alone will soon reach equilibrium but the atoms inside are still flying around.
We are now in a position to state the fundamental assumption of statistical mechanics. It is the idea that we should take the most simple minded approach possible and treat all states the same. Or, more precisely:
| For an isolated system in equilibrium, all accessible microstates are equally likely. |
Since we know nothing else about the system, such a democratic approach seems eminently reasonable. Notice that we’ve left ourselves a little flexibility with the inclusion of the word “accessible”. This refers to any state that can be reached due to the small perturbations felt by the system. For the moment, we will take it mean all states that have the same energy . Later, we shall see contexts where we add further restrictions on what it means to be an accessible state.
Let us introduce some notation. We define
The probability that the system with fixed energy is in a given state is simply
| (1.1) |
The probability that the system is in a state with some different energy is zero. This probability distribution, relevant for systems with fixed energy, is known as the microcanonical ensemble. Some comments:
-
•
is a usually ridiculously large number. For example, suppose that we have particles, each of which can only be in one of two quantum states – say “spin up” and “spin down”. Then the total number of microstates of the system is . This is a silly number. In some sense, numbers this large can never have any physical meaning! They only appear in combinatoric problems, counting possible eventualities. They are never answers to problems which require you to count actual existing physical objects. One, slightly facetious, way of saying this is that numbers this large can’t have physical meaning because they are the same no matter what units they have. (If you don’t believe me, think of as a distance scale: it is effectively the same distance regardless of whether it is measured in microns or lightyears. Try it!).
-
•
In quantum systems, the energy levels will be discrete. However, with many particles the energy levels will be finely spaced and can be effectively treated as a continuum. When we say that counts the number of states with energy we implicitly mean that it counts the number of states with energy between and where is small compared to the accuracy of our measuring apparatus but large compared to the spacing of the levels.
-
•
We phrased our discussion in terms of quantum systems but everything described above readily carries over the classical case. In particular, the probabilities have nothing to do with quantum indeterminacy. They are due entirely to our ignorance.
1.2.1 Entropy and the Second Law of Thermodynamics
We define the entropy of the system to be
| (1.2) |
Here is a fundamental constant, known as Boltzmann’s constant . It has units of Joules per Kelvin.
| (1.3) |
The in (1.2) is the natural logarithm (base , not base 10). Why do we take the log in the definition? One reason is that it makes the numbers less silly. While the number of states is of order , the entropy is merely proportional to the number of particles in the system, . This also has the happy consequence that the entropy is an additive quantity. To see this, consider two non-interacting systems with energies and respectively. Then the total number of states of both systems is
while the entropy for both systems is
The Second Law
Suppose we take the two, non-interacting, systems mentioned above and we bring them together. We’ll assume that they can exchange energy, but that the energy levels of each individual system remain unchanged. (These are actually contradictory assumptions! If the systems can exchange energy then there must be an interaction term in their Hamiltonian. But such a term would shift the energy levels of each system. So what we really mean is that these shifts are negligibly small and the only relevant effect of the interaction is to allow the energy to move between systems).
The energy of the combined system is still . But the first system can have any energy while the second system must have the remainder . In fact, there is a slight caveat to this statement: in a quantum system we can’t have any energy at all: only those discrete energies that are eigenvalues of the Hamiltonian. So the number of available states of the combined system is
| (1.4) | |||||
There is a slight subtlety in the above equation. Both system 1 and system 2 have discrete energy levels. How do we know that if is an energy of system 1 then is an energy of system 2. In part this goes back to the comment made above about the need for an interaction Hamiltonian that shifts the energy levels. In practice, we will just ignore this subtlety. In fact, for most of the systems that we will discuss in this course, the discreteness of energy levels will barely be important since they are so finely spaced that we can treat the energy of the first system as a continuous variable and replace the sum by an integral. We will see many explicit examples of this in the following sections.
At this point, we turn again to our fundamental assumption — all states are equally likely — but now applied to the combined system. This has fixed energy so can be thought of as sitting in the microcanonical ensemble with the distribution (1.1) which means that the system has probability to be in each state. Clearly, the entropy of the combined system is greater or equal to that of the original system,
| (1.5) |
which is true simply because the states of the two original systems are a subset of the total number of possible states.
While (1.5) is true for any two systems, there is a useful approximation we can make to determine which holds when the number of particles, , in the game is very large. We have already seen that the entropy scales as . This means that the expression (1.4) is a sum of exponentials of , which is itself an exponentially large number. Such sums are totally dominated by their maximum value. For example, suppose that for some energy, , the exponent has a value that’s twice as large as any other . Then this term in the sum is larger than all the others by a factor of . And that’s a very large number. All terms but the maximum are completely negligible. (The equivalent statement for integrals is that they can be evaluated using the saddle point method). In our case, the maximum value, , occurs when
| (1.6) |
where this slightly cumbersome notation means (for the first term) evaluated at . The total entropy of the combined system can then be very well approximated by

It’s worth stressing that there is no a priori reason why the first system should have a fixed energy once it is in contact with the second system. But the large number of particles involved means that it is overwhelmingly likely to be found with energy which maximises the number of states of the combined system. Conversely, once in this bigger set of states, it is highly unlikely that the system will ever be found back in a state with energy or, indeed, any other energy different from .
It is this simple statement that is responsible for all the irreversibility that we see in the world around us. This is the second law of thermodynamics. As a slogan, “entropy increases”. When two systems are brought together — or, equivalently, when constraints on a system are removed — the total number of available states available is vastly enlarged.
It is sometimes stated that second law is the most sacred in all of physics. Arthur Eddington’s rant, depicted in the cartoon, is one of the more famous acclamations of the law.
And yet, as we have seen above, the second law hinges on probabilistic arguments. We said, for example, that it is “highly unlikely” that the system will return to its initial configuration. One might think that this may allow us a little leeway. Perhaps, if probabilities are underlying the second law, we can sometimes get lucky and find counterexamples. While, it is most likely to find system 1 to have energy , surely occasionally one sees it in a state with a different energy? In fact, this never happens. The phrase “highly unlikely” is used only because the English language does not contain enough superlatives to stress how ridiculously improbable a violation of the second law would be. The silly number of possible states in a macroscopic systems means that violations happen only on silly time scales: exponentials of exponentials. This is a good operational definition of the word “never”.
1.2.2 Temperature
We next turn to a very familiar quantity, albeit viewed in an unfamiliar way. The temperature, , of a system is defined as
| (1.7) |
This is an extraordinary equation. We have introduced it as the definition of temperature. But why is this a good definition? Why does it agree with the idea of temperature that your mum has? Why is this the same that makes mercury rise (the element, not the planet…that’s a different course.) Why is it the same that makes us yell when we place our hand on a hot stove?
First, note that has the right units, courtesy of Boltzmann’s constant (1.3). But that was merely a choice of convention: it doesn’t explain why has the properties that we expect of temperature. To make progress, we need to think more carefully about the kind of properties that we do expect. We will describe this in some detail in Section 4. For now it will suffice to describe the key property of temperature, which is the following: suppose we take two systems, each in equilibrium and each at the same temperature , and place them in contact so that they can exchange energy. Then …nothing happens.
It is simple to see that this follows from our definition (1.7). We have already done the hard work above where we saw that two systems, brought into contact in this way, will maximize their entropy. This is achieved when the first system has energy and the second energy , with determined by equation (1.6). If we want nothing noticeable to happen when the systems are brought together, then it must have been the case that the energy of the first system was already at . Or, in other words, that equation (1.6) was obeyed before the systems were brought together,
| (1.8) |
From our definition (1.7), this is the same as requiring that the initial temperatures of the two systems are equal: .
Suppose now that we bring together two systems at slightly different temperatures. They will exchange energy, but conservation ensures that what the first system gives up, the second system receives and vice versa. So . If the change of entropy is small, it is well approximated by
The second law tells us that entropy must increase: . This means that if , we must have . In other words, the energy flows in the way we would expect: from the hotter system to colder.
To summarise: the equilibrium argument tell us that should have the interpretation as some function of temperature; the heat flowing argument tell us that it should be a monotonically decreasing function. But why and not, say, ? To see this, we really need to compute for a system that we’re all familiar with and see that it gives the right answer. Once we’ve got the right answer for one system, the equilibrium argument will ensure that it is right for all systems. Our first business in Section 2 will be to compute the temperature for an ideal gas and confirm that (1.7) is indeed the correct definition.
Heat Capacity
The heat capacity, , is defined by
| (1.9) |
We will later introduce more refined versions of the heat capacity (in which various, yet-to-be-specified, external parameters are held constant or allowed to vary and we are more careful about the mode of energy transfer into the system). The importance of the heat capacity is that it is defined in terms of things that we can actually measure! Although the key theoretical concept is entropy, if you’re handed an experimental system involving particles, you can’t measure the entropy directly by counting the number of accessible microstates. You’d be there all day. But you can measure the heat capacity: you add a known quantity of energy to the system and measure the rise in temperature. The result is .
There is another expression for the heat capacity that is useful. The entropy is a function of energy, . But we could invert the formula (1.7) to think of energy as a function of temperature, . We then have the expression
This is a handy formula. If we can measure the heat capactiy of the system for various temperatures, we can get a handle on the function . From this we can then determine the entropy of the system. Or, more precisely, the entropy difference
| (1.10) |
Thus the heat capacity is our closest link between experiment and theory.
The heat capacity is always proportional to , the number of particles in the system. It is common to define the specific heat capacity, which is simply the heat capacity divided by the mass of the system and is independent of .
There is one last point to make about heat capacity. Differentiating (1.7) once more, we have
| (1.11) |
Nearly all systems you will meet have . (There is one important exception: a black hole has negative heat capacity!). Whenever , the system is said to be thermodynamically stable. The reason for this language goes back to the previous discussion concerning two systems which can exchange energy. There we wanted to maximize the entropy and checked that we had a stationary point (1.6), but we forgot to check whether this was a maximum or minimum. It is guaranteed to be a maximum if the heat capacity of both systems is positive so that .
1.2.3 An Example: The Two State System
Consider a system of non-interacting particles. Each particle is fixed in position and can sit in one of two possible states which, for convenience, we will call “spin up” and “spin down” . We take the energy of these states to be,
which means that the spins want to be down; you pay an energy cost of for each spin which points up. If the system has particles with spin up and particles with spin down, the energy of the system is
We can now easily count the number of states of the total system which have energy . It is simply the number of ways to pick particles from a total of ,
and the entropy is given by
An Aside: Stirling’s Formula
For large , there is a remarkably accurate approximation to the factorials that appear in the expression for the entropy. It is known as Stirling’s formula,
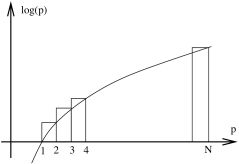
You will prove this on the first problem sheet. However, for our purposes we will only need the first two terms in this expansion and these can be very quickly derived by looking at the expression
where we have approximated the sum by the integral as shown in the figure. You can also see from the figure that integral gives a lower bound on the sum which is confirmed by checking the next terms in Stirling’s formula.
Back to the Physics
Using Stirling’s approximation, we can write the entropy as
| (1.12) | |||||
A sketch of plotted against is shown in Figure 3. The entropy vanishes when (all spins down) and (all spins up) because there is only one possible state with each of these energies. The entropy is maximal when where we have .
If the system has energy , its temperature is
We can also invert this expression. If the system has temperature , the fraction of particles with spin up is given by
| (1.13) |
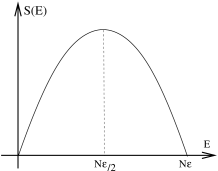
Note that as , the fraction of spins . In the limit of infinite temperature, the system sits at the peak of the curve in Figure 3.
What happens for energies , where ? From the definition of temperature as , it is clear that we have entered the realm of negative temperatures. This should be thought of as hotter than infinity! (This is simple to see in the variables which tends towards zero and then just keeps going to negative values). Systems with negative temperatures have the property that the number of microstates decreases as we add energy. They can be realised in laboratories, at least temporarily, by instantaneously flipping all the spins in a system.
Heat Capacity and the Schottky Anomaly
Finally, we can compute the heat capacity, which we choose to express as a function of temperature (rather than energy) since this is more natural when comparing to experiment. We then have
| (1.14) |
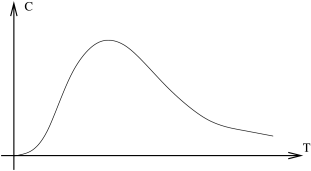
Note that is of order , the number of particles in the system. This property extends to all other examples that we will study. A sketch of vs is shown in Figure 4. It starts at zero, rises to a maximum, then drops off again. We’ll see a lot of graphs in this course that look more or less like this. Let’s look at some of the key features in this case. Firstly, the maximum is around . In other words, the maximum point sits at the characteristic energy scale in the system.
As , the specific heat drops to zero exponentially quickly. (Recall that is a function which tends towards zero faster than any power ). The reason for this fast fall-off can be traced back to the existence of an energy gap, meaning that the first excited state is a finite energy above the ground state. The heat capacity also drops off as , but now at a much slower power-law pace. This fall-off is due to the fact that all the states are now occupied.
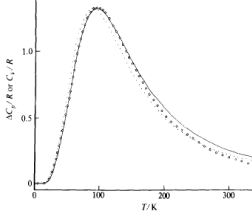
The contribution to the heat capacity from spins is not the dominant contribution in most materials. It is usually dwarfed by the contribution from phonons and, in metals, from conduction electrons, both of which we will calculate later in the course. Nonetheless, in certain classes of material — for example, paramagnetic salts — a spin contribution of the form (1.14) can be seen at low temperatures where it appears as a small bump in the graph and is referred to as the Schottky anomaly. (It is ‘‘anomalous” because most materials have a heat capacity which decreases monotonically as temperature is reduced). In Figure 5, the Schottky contribution has been isolated from the phonon contribution11 1 The data is taken from Chirico and Westrum Jr., J. Chem. Thermodynamics 12 (1980), 311, and shows the spin contribution to the heat capacity of Tb(OH). The open circles and dots are both data (interpreted in mildly different ways); the solid line is theoretical prediction, albeit complicated slightly by the presence of a number of spin states. The deviations are most likely due to interactions between the spins.
The two state system can also be used as a model for defects in a lattice. In this case, the “spin down” state corresponds to an atom sitting in the lattice where it should be with no energy cost. The “spin up” state now corresponds to a missing atom, ejected from its position at energy cost .
1.2.4 Pressure, Volume and the First Law of Thermodynamics
We will now start to consider other external parameters which can affect different systems. We will see a few of these as we move through the course, but the most important one is perhaps the most obvious – the volume of a system. This didn’t play a role in the two-state example because the particles were fixed. But as soon as objects are free to move about, it becomes crucial to understand how far they can roam.
We’ll still use the same notation for the number of states and entropy of the system, but now these quantities will be functions of both the energy and the volume,
The temperature is again given by , where the partial derivative implicitly means that we keep fixed when we differentiate. But now there is a new, natural quantity that we can consider — the differentiation with respect to . This also gives a quantity that you’re all familiar with — pressure, . Well, almost. The definition is
| (1.15) |
To see that this is a sensible definition, we can replay the arguments of Section 1.2.2. Imagine two systems in contact through a moveable partition as shown in the figure above, so that the total volume remains fixed, but system 1 can expand at the expense of system 2 shrinking. The same equilibrium arguments that previously lead to (1.8) now tell us that the volumes of the systems don’t change as long as is the same for both systems. Or, in other words, as long as the pressures are equal.
Despite appearances, the definition of pressure actually has little to do with entropy. Roughly speaking, the in the derivative cancels the factor of sitting in . To make this mathematically precise, consider a system with entropy that undergoes a small change in energy and volume. The change in entropy is
Rearranging, and using our definitions (1.7) and (1.15), we can write
| (1.16) |
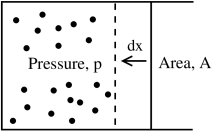
The left-hand side is the change in energy of the system. It is easy to interpret the second term on the right-hand side: it is the work done on the system. To see this, consider the diagram on the right. Recall that pressure is force per area. The change of volume in the set-up depicted is . So the work done on the system is . To make sure that we’ve got the minus signs right, remember that if , we’re exerting a force to squeeze the system, increasing its energy. In contrast, if , the system itself is doing the work and hence losing energy.
Alternatively, you may prefer to run this argument in reverse: if you’re happy to equate squeezing the system by with doing work, then the discussion above is sufficient to tell you that pressure as defined in (1.15) has the interpretation of force per area.
What is the interpretation of the first term on the right-hand side of (1.16)? It must be some form of energy transferred to the system. It turns out that the correct interpretation of is the amount of heat the system absorbs from the surroundings. Much of Section 4 will be concerned with understanding why this is right way to think about and we postpone a full discussion until then.
As a final comment, we can now give a slightly more refined definition of the heat capacity (1.9). In fact, there are several different heat capacities which depend on which other variables are kept fixed. Throughout most of these lectures, we will be interested in the heat capacity at fixed volume, denoted ,
| (1.17) |
Using the first law of thermodynamics (1.16), we see that something special happens when we keep volume constant: the work done term drops out and we have
| (1.18) |
This form emphasises that, as its name suggests, the heat capacity measures the ability of the system to absorb heat as opposed to any other form of energy. (Although, admittedly, we still haven’t really defined what heat is. As mentioned above, this will have to wait until Section 4).
The equivalence of (1.17) and (1.18) only followed because we kept volume fixed. What is the heat capacity if we keep some other quantity, say pressure, fixed? In this case, the correct definition of heat capacity is the expression analogous to (1.18). So, for example, the heat capacity at constant pressure is defined by
For the next few Sections, we’ll only deal with . But we’ll return briefly to the relationship between and in Section 4.4.
1.2.5 Ludwig Boltzmann (1844-1906)
“My memory for figures, otherwise tolerably accurate, always lets me down when I am counting beer glasses”
Boltzmann Counting
Ludwig Boltzmann was born into a world that doubted the existence of atoms22 2 If you want to learn more about his life, I recommend the very enjoyable biography, Boltzmann’s Atom by David Lindley. The quote above is taken from a travel essay that Boltzmann wrote recounting a visit to California. The essay is reprinted in a drier, more technical, biography by Carlo Cercignani.. The cumulative effect of his lifetime’s work was to change this. No one in the 1800s ever thought we could see atoms directly and Boltzmann’s strategy was to find indirect, yet overwhelming, evidence for their existence. He developed much of the statistical machinery that we have described above and, building on the work of Maxwell, showed that many of the seemingly fundamental laws of Nature — those involving heat and gases in particular — were simply consequences of Newton’s laws of motion when applied to very large systems.
It is often said that Boltzmann’s great insight was the equation which is now engraved on his tombstone, , which lead to the understanding of the second law of thermodynamics in terms of microscopic disorder. Yet these days it is difficult to appreciate the boldness of this proposal simply because we rarely think of any other definition of entropy. We will, in fact, meet the older thermodynamic notion of entropy and the second law in Section 4. In the meantime, perhaps Boltzmann’s genius is better reflected in the surprising equation for temperature: .
Boltzmann gained prominence during his lifetime, holding professorships at Graz, Vienna, Munich and Leipzig (not to mention a position in Berlin that he somehow failed to turn up for). Nonetheless, his work faced much criticism from those who would deny the existence of atoms, most notably Mach. It is not known whether these battles contributed to the depression Boltzmann suffered later in life, but the true significance of his work was only appreciated after his body was found hanging from the rafters of a guest house near Trieste.
1.3 The Canonical Ensemble
The microcanonical ensemble describes systems that have a fixed energy . From this, we deduce the equilibrium temperature . However, very often this is not the best way to think about a system. For example, a glass of water sitting on a table has a well defined average energy. But the energy is constantly fluctuating as it interacts with the environment. For such systems, it is often more appropriate to think of them as sitting at fixed temperature , from which we then deduce the average energy.
To model this, we will consider a system — let’s call it — in contact with a second system which is a large heat reservoir – let’s call it . This reservoir is taken to be at some equilibrium temperature . The term “reservoir” means that the energy of is negligible compared with that of . In particular, can happily absorb or donate energy from or to the reservoir without changing the ambient temperature .
How are the energy levels of populated in such a situation? We label the states of as , each of which has energy . The number of microstates of the combined systems and is given by the sum over all states of ,
I stress again that the sum above is over all the states of , rather than over the energy levels of . (If we’d written the latter, we would have to include a factor of in the sum to take into account the degeneracy of states with energy ). The fact that is a reservoir means that . This allows us to Taylor expand the entropy, keeping just the first two terms,
But we know that , so we have
We now apply the fundamental assumption of statistical mechanics — that all accessible energy states are equally likely — to the combined system + reservoir. This means that each of the states above is equally likely. The number of these states for which the system sits in is . So the probabilty that the system sits in state is just the ratio of this number of states to the total number of states,
| (1.19) |
This is the Boltzmann distribution, also known as the canonical ensemble. Notice that the details of the reservoir have dropped out. We don’t need to know for the reservoir; all that remains of its influence is the temperature .
The exponential suppression in the Boltzmann distribution means that it is very unlikely that any of the states with are populated. However, all states with energy have a decent chance of being occupied. Note that as , the Boltzmann distribution forces the system into its ground state (i.e. the state with lowest energy); all higher energy states have vanishing probability at zero temperature.
1.3.1 The Partition Function
Since we will be using various quantities a lot, it is standard practice to introduce new notation. Firstly, the inverse factor of the temperature is universally denoted,
| (1.20) |
And the normalization factor that sits in the denominator of the probability is written,
| (1.21) |
In this notation, the probability for the system to be found in state is
| (1.22) |
Rather remarkably, it turns out that the most important quantity in statistical mechanics is . Although this was introduced as a fairly innocuous normalization factor, it actually contains all the information we need about the system. We should think of , as defined in (1.21), as a function of the (inverse) temperature . When viewed in this way, is called the partition function.
We’ll see lots of properties of soon. But we’ll start with a fairly basic, yet important, point: for independent systems, ’s multiply. This is easy to prove. Suppose that we have two systems which don’t interact with each other. The energy of the combined system is then just the sum of the individual energies. The partition function for the combined system is (in, hopefully, obvious notation)
| (1.23) | |||||
A Density Matrix for the Canonical Ensemble
In statistical mechanics, the inherent probabilities of the quantum world are joined with probabilities that arise from our ignorance of the underlying state. The correct way to describe this is in term of a density matrix, . The canonical ensemble is really a choice of density matrix,
| (1.24) |
If we make a measurement described by an operator , then the probability that we find ourselves in the eigenstate is given by
For energy eigenstates, this coincides with our earlier result (1.22). We won’t use the language of density matrices in this course, but it is an elegant and conceptually clear framework to describe more formal results.
1.3.2 Energy and Fluctuations
Let’s see what information is contained in the partition function. We’ll start by thinking about the energy. In the microcanonical ensemble, the energy was fixed. In the canonical ensemble, that is no longer true. However, we can happily compute the average energy,
But this can be very nicely expressed in terms of the partition function by
| (1.25) |
We can also look at the spread of energies about the mean — in other words, about fluctuations in the probability distribution. As usual, this spread is captured by the variance,
This too can be written neatly in terms of the partition function,
| (1.26) |
There is another expression for the fluctuations that provides some insight. Recall our definition of the heat capacity (1.9) in the microcanonical ensemble. In the canonical ensemble, where the energy is not fixed, the corresponding definition is
Then, since , the spread of energies in (1.26) can be expressed in terms of the heat capacity as
| (1.27) |
There are two important points hiding inside this small equation. The first is that the equation relates two rather different quantities. On the left-hand side, describes the probabilistic fluctuations in the energy of the system. On the right-hand side, the heat capacity describes the ability of the system to absorb energy. If is large, the system can take in a lot of energy without raising its temperature too much. The equation (1.27) tells us that the fluctuations of the systems are related to the ability of the system to dissipate, or absorb, energy. This is the first example of a more general result known as the fluctuation-dissipation theorem.
The other point to take away from (1.27) is the size of the fluctuations as the number of particles in the system increases. Typically and . Which means that the relative size of the fluctuations scales as
| (1.28) |
The limit in known as the thermodynamic limit. The energy becomes peaked closer and closer to the mean value and can be treated as essentially fixed. But this was our starting point for the microcanonical ensemble. In the thermodynamic limit, the microcanonical and canonical ensembles coincide.
All the examples that we will discuss in the course will have a very large number of particles, , and we can consider ourselves safely in the thermodynamic limit. For that reason, even in the canonical ensemble, we will often write for the average energy rather than .
An Example: The Two State System Revisited
We can rederive our previous results for the two state system using the canonical ensemble. It is marginally simpler. For a single particle with two energy levels, and , the partition function is given by
We want the partition function for such particles. But we saw in (1.23) that if we have independent systems, then we simply need to multiply their partition functions together. We then have
from which we can easily compute the average energy
A bit of algebra will reveal that this is the same expression that we derived in the microcanonical ensemble (1.13). We could now go on to compute the heat capacity and reproduce the result (1.14).
Notice that, unlike in the microcanonical ensemble, we didn’t have to solve any combinatoric problem to count states. The partition function has done all that work for us. Of course, for this simple two state system, the counting of states wasn’t difficult but in later examples, where the counting gets somewhat tricker, the partition function will be an invaluable tool to save us the work.
1.3.3 Entropy
Recall that in the microcanonical ensemble, the entropy counts the (log of the) number of states with fixed energy. We would like to define an analogous quantity in the canonical ensemble where we have a probability distribution over states with different energies. How to proceed? Our strategy will be to again return to the microcanonical ensemble, now applied to the combined system + reservoir.
In fact, we’re going to use a little trick. Suppose that we don’t have just one copy of our system , but instead a large number, , of identical copies. Each system lives in a particular state . If is large enough, the number of systems that sit in state must be simply . We see that the trick of taking copies has translated the probabilities into eventualities. To determine the entropy we can treat the whole collection of systems as sitting in the microcanonical ensemble to which we can apply the familiar Boltzmann definition of entropy (1.2). We must only figure out how many ways there are of putting systems into state for each . That’s a simple combinatoric problem: the answer is
And the entropy is therefore
| (1.29) |
where we have used Stirling’s formula to simplify the logarithms of factorials. This is the entropy for all copies of the system. But we also know that entropy is additive. So the entropy for a single copy of the system, with probability distribution over the states is
| (1.30) |
This beautiful formula is due to Gibbs. It was rediscovered some decades later in the context of information theory where it goes by the name of Shannon entropy for classical systems or von Neumann entropy for quantum systems. In the quantum context, it is sometimes written in terms of the density matrix (1.24) as
When we first introduced entropy in the microcanonical ensemble, we viewed it as a function of the energy . But (1.30) gives a very different viewpoint on the entropy: it says that we should view as a function of a probability distribution. There is no contradiction with the microcanonical ensemble because in that simple case, the probability distribution is itself determined by the choice of energy . Indeed, it is simple to check (and you should!) that the Gibbs entropy (1.30) reverts to the Boltzmann entropy in the special case of for all states of energy .
Meanwhile, back in the canonical ensemble, the probability distribution is entirely determined by the choice of temperature . This means that the entropy is naturally a function of . Indeed, substituting the Boltzmann distribution into the expression (1.30), we find that the entropy in the canonical ensemble is given by
As with all other important quantities, this can be elegantly expressed in terms of the partition function by
| (1.31) |
A Comment on the Microcanonical vs Canonical Ensembles
The microcanonical and canonical ensembles are different probability distributions. This means, using the definition (1.30), that they generally have different entropies. Nonetheless, in the limit of a large number of particles, , all physical observables — including entropy — coincide in these two distributions. We’ve already seen this when we computed the variance of energy (1.28) in the canonical ensemble. Let’s take a closer look at how this works.
The partition function in (1.21) is a sum over all states. We can rewrite it as a sum over energy levels by including a degeneracy factor
The degeneracy factor factor is typically a rapidly rising function of , while the Boltzmann suppression is rapidly falling. But, for both the exponent is proportional to which is itself exponentially large. This ensures that the sum over energy levels is entirely dominated by the maximum value, , defined by the requirement
and the partition function can be well approximated by
(This is the same kind of argument we used in (1.2.1) in our discussion of the Second Law). With this approximation, we can use (1.25) to show that the most likely energy and the average energy coincide:
(We need to use the result (1.7) in the form to derive this). Similarly, using (1.31), we can show that the entropy in the canonical ensemble is given by
Maximizing Entropy
There is actually a unified way to think about the microcanonical and canonical ensembles in terms of a variational principle: the different ensembles have the property that they maximise the entropy subject to various constraints. The only difference between them is the constraints that are imposed.
Let’s start with the microcanonical ensemble, in which we fix the energy of the system so that we only allow non-zero probabilities for those states which have energy . We could then compute the entropy using the Gibbs formula (1.30) for any probability distribution, including systems away from equilibrium. We need only insist that all the probabilities add up to one: . We can maximise subject to this condition by introducing a Lagrange multiplier and maximising ,
We learn that all states with energy are equally likely. This is the microcanonical ensemble.
In the examples sheet, you will be asked to show that the canonical ensemble can be viewed in the same way: it is the probability distribution that maximises the entropy subject to the constraint that the average energy is fixed.
1.3.4 Free Energy
We’ve left the most important quantity in the canonical ensemble to last. It is called the free energy,
| (1.32) |
There are actually a number of quantities all vying for the name “free energy”, but the quantity is the one that physicists usually work with. When necessary to clarify, it is sometimes referred to as the Helmholtz free energy. The word “free” here doesn’t mean “without cost”. Energy is never free in that sense. Rather, it should be interpreted as the “available” energy.
Heuristically, the free energy captures the competition between energy and entropy that occurs in a system at constant temperature. Immersed in a heat bath, energy is not necessarily at a premium. Indeed, we saw in the two-state example that the ground state plays little role in the physics at non-zero temperature. Instead, the role of entropy becomes more important: the existence of many high energy states can beat a few low-energy ones.
The fact that the free energy is the appropriate quantity to look at for systems at fixed temperature is also captured by its mathematical properties. Recall, that we started in the microcanonical ensemble by defining entropy . If we invert this expression, then we can equally well think of energy as a function of entropy and volume: . This is reflected in the first law of thermodynamics (1.16) which reads . However, if we look at small variations in , we get
| (1.33) |
This form of the variation is telling us that we should think of the free energy as a function of temperature and volume: . Mathematically, is a Legendre transform of .
Given the free energy, the variation (1.33) tells us how to get back the entropy,
| (1.34) |
Similarly, the pressure is given by
| (1.35) |
The free energy is the most important quantity at fixed temperature. It is also the quantity that is most directly related to the partition function :
| (1.36) |
This relationship follows from (1.25) and (1.31). Using the identity , these expressions allow us to write the free energy as
as promised.
1.4 The Chemical Potential
Before we move onto applications, there is one last bit of formalism that we will need to introduce. This arises in situations where there is some other conserved quantity which restricts the states that are accessible to the system. The most common example is simply the number of particles in the system. Another example is the electric charge . For the sake of definiteness, we will talk about particle number below but all the comments apply to any conserved quantity.
In both the microcanonical and canonical ensembles, we should only consider states that have a fixed value of . We already did this when we discussed the two state system — for example, the expression for entropy (1.12) depends explicitly on the number of particles . We will now make this dependence explicit and write
The entropy leads us to the temperature as and the pressure as . But now we have another option: we can differentiate with respect to particle number . The resulting quantity is called the chemical potential,
| (1.37) |
Using this definition, we can re-run the arguments given in Section 1.2.2 for systems which are allowed to exchange particles. Such systems are in equilibrium only if they have equal chemical potential . This condition is usually referred to as chemical equilibrium.
To get a feel for the meaning of the chemical potential, we can look again at the first law of thermodynamics (1.16), now allowing for a change in particle number as well. Writing and rearranging, we have,
| (1.38) |
This tells us the meaning of the chemical potential: it is the energy cost to add one more particle to the system while keeping both and fixed. (Strictly speaking, an infinitesimal amount of particle, but if we’re adding one more to that effectively counts as infinitesimal). If we’re interested in electric charge , rather than particle number, the chemical potential is the same thing as the familiar electrostatic potential of the system that you met in your first course in Electromagnetism.
There’s actually a subtle point in the above derivation that is worth making explicit. It’s the kind of thing that will crop up a lot in thermodynamics where you typically have many variables and need to be careful about which ones are kept fixed. We defined the chemical potential as . But the first law is telling us that we can also think of the chemical potential as . Why is this the same thing? This follows from a general formula for partial derivatives. If you have three variables, , and , with a single constraint between them, then
Applying this general formula to , and gives us the required result
If we work at constant temperature rather than constant energy, the relevant function is the free energy . Small changes are given by
from which we see that the chemical potential can also be defined as
1.4.1 Grand Canonical Ensemble
When we made the transition from microcanonical to canonical ensemble, we were no longer so rigid in our insistence that the system has a fixed energy. Rather it could freely exchange energy with the surrounding reservoir, which was kept at a fixed temperature. We could now imagine the same scenario with any other conserved quantity. For example, if particles are free to move between the system and the reservoir, then is no longer fixed. In such a situation, we will require that the reservoir sits at fixed chemical potential as well as fixed temperature .
The probability distribution that we need to use in this case is called the grand canonical ensemble. The probability of finding the system in a state depends on both the energy and the particle number . (Notice that because is conserved, the quantum mechanical operator necessarily commutes with the Hamiltonian so there is no difficulty in assigning both energy and particle number to each state). We introduce the grand canonical partition function
| (1.39) |
Re-running the argument that we used for the canonical ensemble, we find the probability that the system is in state to be
In the canonical ensemble, all the information that we need is contained within the partition function . In the grand canonical ensemble it is contained within . The entropy (1.30) is once again given by
| (1.40) |
while differentiating with respect to gives us
| (1.41) |
The average particle number in the system can then be separately extracted by
| (1.42) |
and its fluctuations,
| (1.43) |
Just as the average energy is determined by the temperature in the canonical ensemble, here the average particle number is determined by the chemical potential. The grand canonical ensemble will simplify several calculations later, especially when we come to discuss Bose and Fermi gases in Section 3.
The relative size of these fluctuations scales in the same way as the energy fluctuations, , and in the thermodynamic limit results from all three ensembles coincide. For this reason, we will drop the averaging brackets from our notation and simply refer to the average particle number as .
1.4.2 Grand Canonical Potential
The grand canonical potential is defined by
is a Legendre transform of , from variable to . This is underlined if we look at small variations,
| (1.44) |
which tells us that should be thought of as a function of temperature, volume and chemical potential, .
1.4.3 Extensive and Intensive Quantities
There is one property of that is rather special and, at first glance, somewhat surprising. This property actually follows from very simple considerations of how different variables change as we look at bigger and bigger systems.
Suppose we have a system and we double it. That means that we double the volume , double the number of particles and double the energy . What happens to all our other variables? We have already seen back in Section 1.2.1 that entropy is additive, so also doubles. More generally, if we scale , and by some amount , the entropy must scale as
Quantities such as , , and which scale in this manner are called extensive. In contrast, the variables which arise from differentiating the entropy, such as temperature and pressure and chemical potential involve the ratio of two extensive quantities and so do not change as we scale the system: they are called intensive quantities.
What now happens as we make successive Legendre transforms? The free energy is also extensive (since and are extensive while is intensive). So it must scale as
| (1.46) |
Similarly, the grand potential is extensive and scales as
| (1.47) |
But there’s something special about this last equation, because only depends on a single extensive variable, namely . While there are many ways to construct a free energy which obeys (1.46) (for example, any function of the form will do the job), there is only one way to satisfy (1.47): must be proportional to . But we’ve already got a name for this proportionality constant: it is pressure. (Actually, it is minus the pressure as you can see from (1.44)). So we have the equation
| (1.48) |
It looks as if we got something for free! If is a complicated function of , where do these complications go after the Legendre transform to ? The answer is that the complications go into the pressure when expressed as a function of and . Nonetheless, equation (1.48) will prove to be an extremely economic way to calculate the pressure of various systems.
1.4.4 Josiah Willard Gibbs (1839-1903)
“Usually, Gibbs’ prose style conveys his meaning in a sufficiently clear way, using no more than twice as many words as Poincaré or Einstein would have used to say the same thing.”
E.T.Jaynes on the difficulty of reading Gibbs
Gibbs was perhaps the first great American theoretical physicist. Many of the developments that we met in this chapter are due to him, including the free energy, the chemical potential and, most importantly, the idea of ensembles. Even the name “statistical mechanics” was invented by Gibbs.
Gibbs provided the first modern rendering of the subject in a treatise published shortly before his death. Very few understood it. Lord Rayleigh wrote to Gibbs suggesting that the book was “too condensed and too difficult for most, I might say all, readers”. Gibbs disagreed. He wrote back saying the book was only “too long”.
There do not seem to be many exciting stories about Gibbs. He was an undergraduate at Yale. He did a PhD at Yale. He became a professor at Yale. Apparently he rarely left New Haven. Strangely, he did not receive a salary for the first ten years of his professorship. Only when he received an offer from John Hopkins of $3000 dollars a year did Yale think to pay America’s greatest physicist. They made a counter-offer of $2000 dollars and Gibbs stayed.