We identify four flow states in this experiment, depending on the fractional density differences, characterised by the dimensionless Atwood number, and the angle of inclination $\theta$, which is defined to be positive (negative) when the along-duct component of gravity reinforces (opposes) the buoyancy-induced pressure differences across the ends of the duct. For sufficiently negative angles and small fractional density differences the flow is observed to be laminar ($\mathsf{L}$ state) with an undisturbed density interface separating the two layers. For positive angles and/or high fractional density differences three other states are observed. For small angles of inclination the flow is wave-dominated and exhibits Holmboe modes ($\mathsf{H}$ state) on the interface with characteristic cusp-like wave breaking. At the highest positive angles and density differences there is a turbulent ($\mathsf{T}$ state) high-dissipation interfacial region typically containing Kelvin-Helmholtz (KH)-like structures sheared in the direction of the mean shear and connecting both layers. For intermediate angles and density differences an intermittent state ($\mathsf{I}$ state) is found, which exhibits a rich range of spatio-temporal behaviour and an interfacial region that contains features of KH-like structures and of the other two lower-dissipation states: thin interfaces and Holmboe-like structures. We map the state diagram of these flows in the Atwood number -- $\theta$ plane and examine the force balances that determine each of these states. We find that the $\mathsf{L}$ and $\mathsf{H}$ states are hydraulically controlled at the ends of the duct and the flow is determined by the pressure difference associated with the density difference between the reservoirs. As the inclination increases, the along-slope component of the buoyancy force becomes more significant and the $\mathsf{I}$ and $\mathsf{T}$ states are associated with increasing dissipation within the duct. We replot the state-space in the Grashof number -- $\theta$ phase plane and find the transition to the $\mathsf{T}$-state is governed by a critical Grashof number. We find that the corresponding buoyancy Reynolds number of the transition to the $\mathsf{T}$-state is of order 100, and that this state is also found to be hydraulically controlled at the ends of the duct. In this state the dissipation balances the force associated with the along-slope component of buoyancy and the counterflow has a critical composite Froude number.

We have carried out matched pairs of experiments in which we separately measure the velocity and density fields, over the range of states observed in SID. Examples can be seen in the movies. The analysis of these data is on going.

Although turbulence is generally suppressed in very statically stable conditions, intermittent bursts of turbulence are still seen when the Reynolds number is sufficiently large. We study stratified turbulence in plane Couette flow using direct numerical simulations, focusing on the complexity arising from the spatio-temporal intermittency of the flow as the stabilizing stratification increases. Two external dimensionless parameters control the dynamics: the Reynolds number $Re$ and the bulk Richardson number $Ri_b$. We trace the boundary between laminar and turbulent states in the $Re$ , $Ri_b$ plane and discuss the relevant dynamical quantities involved in the relaminarization process. The aim is on analyzing the structures populating the intermittent regime and the coexistence between laminar and turbulent patches, focusing on similarities and differences between small-$Re$ small $Ri_b$ and large $Re$ large $Ri_b$ intermittent dynamics. We also aim at investigating the applicability and breakdown of existing stratified turbulence theories, including the Monin-Obukhov self-similarity theory and stratified variation of TKE models.

Wall-bounded shear flows typically follow a subcritical transition scenario where finite amplitude solutions unconnected to the basic flow play a key role. Edge tracking has been very useful in finding some of these by following the laminar-turbulent boundary in phase space for many canonical shear flows. However, it has yet to be used to probe stratified flows. In this project we investigate the results of edge tracking in stably-stratified plane Couette flow over large and small domains (click here for a movie).

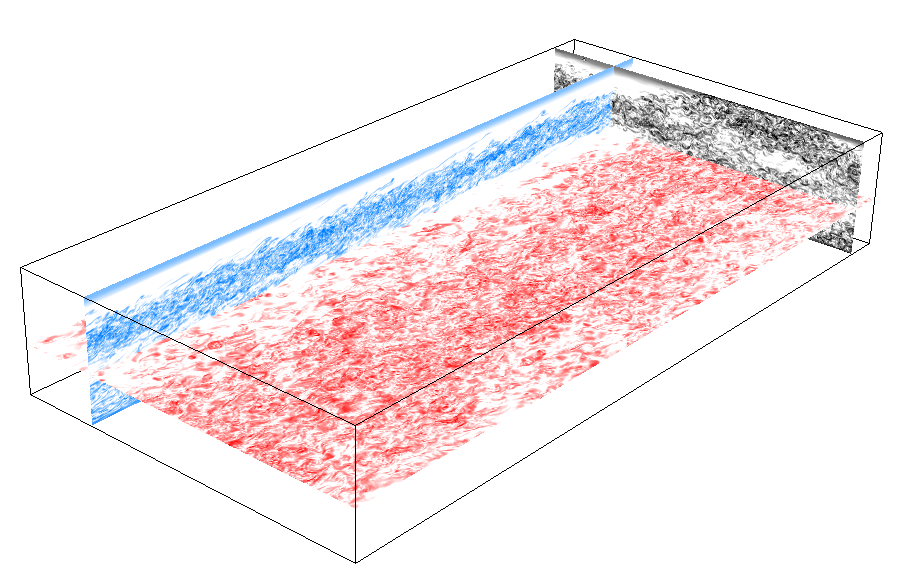
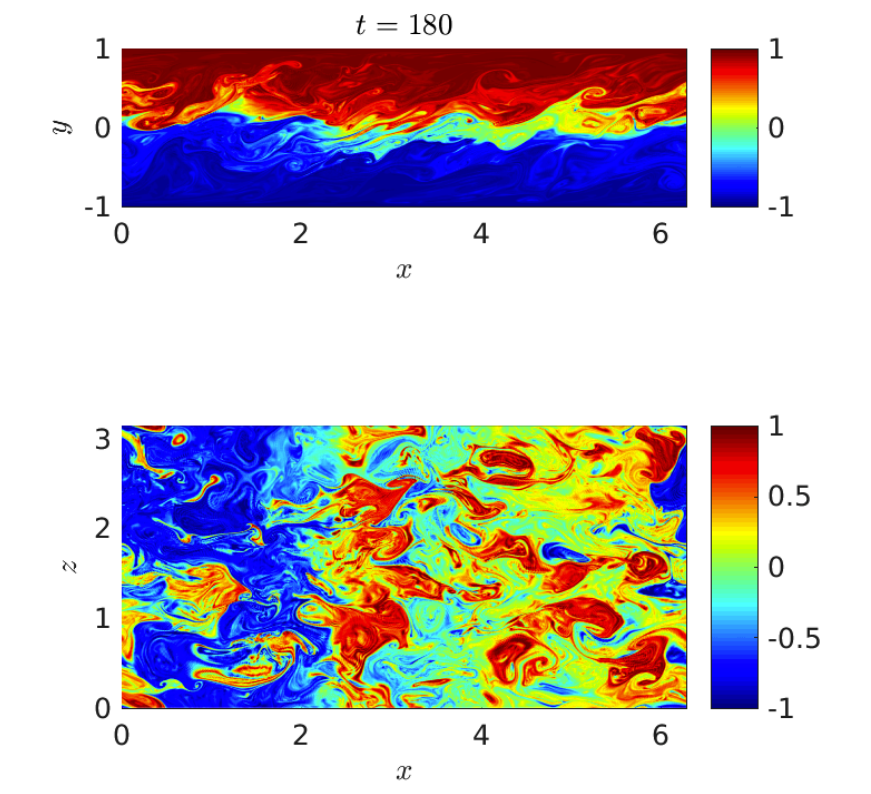
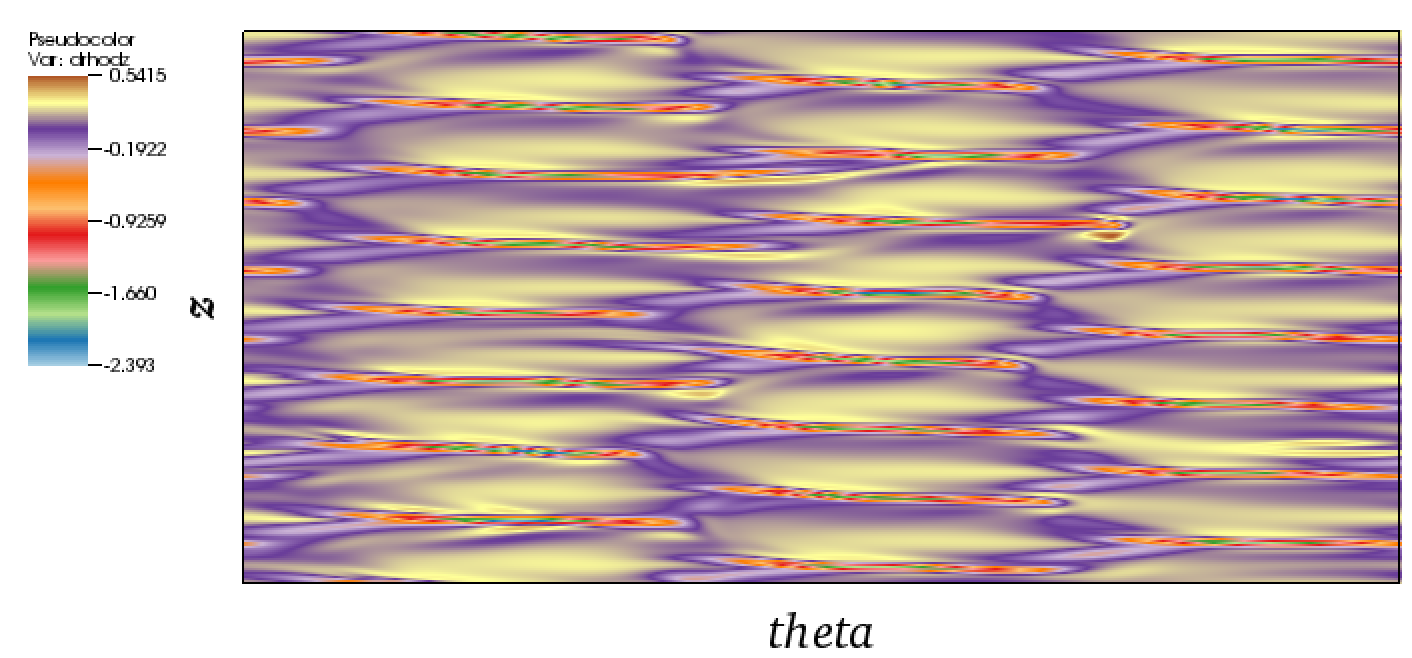
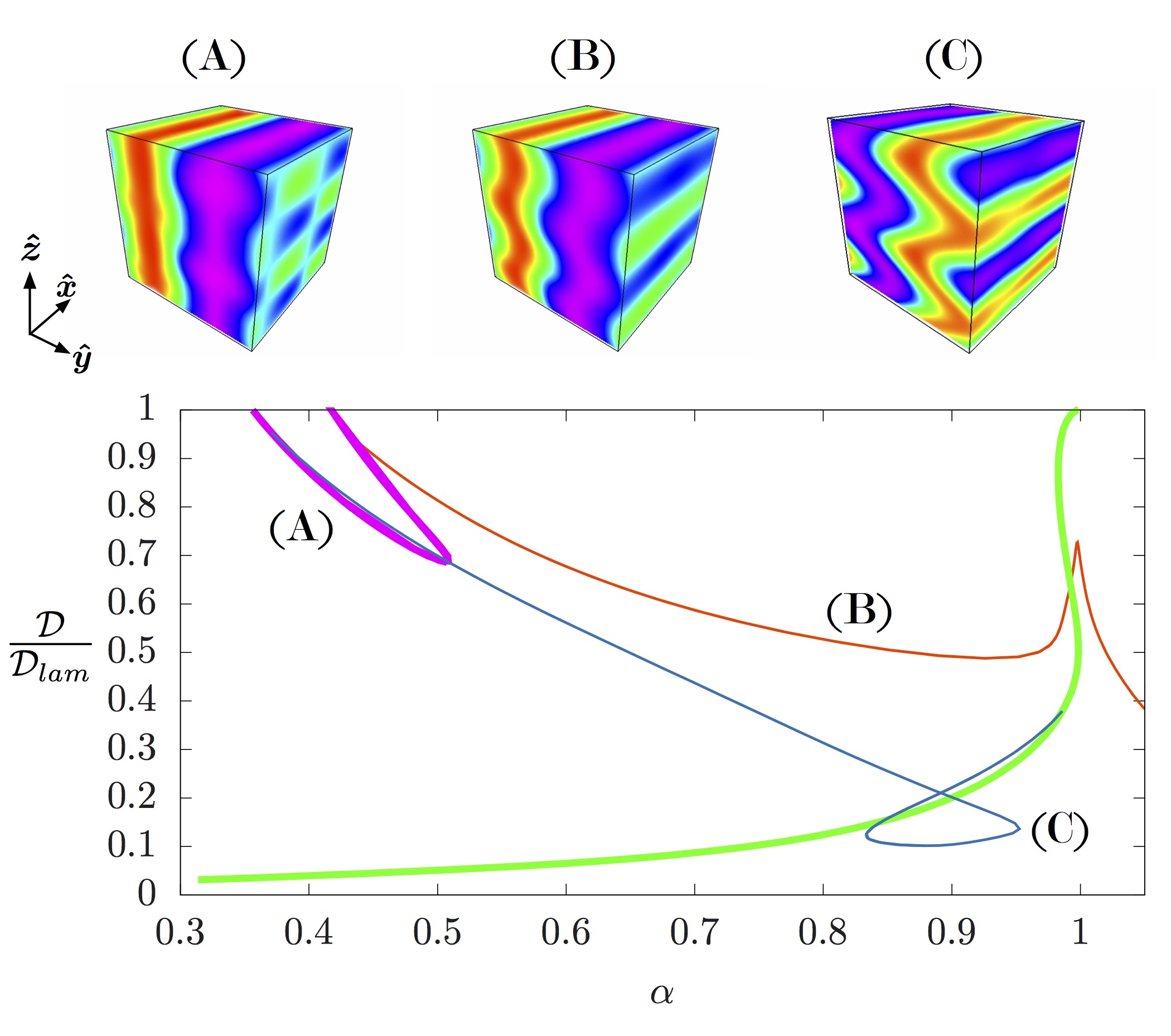
The stability properties of shear flows have received wide attention due to the important engineering applications of understanding how and when turbulence might emerge in a given flow geometry. Research has recently focused on identifying "minimal seeds," i.e. the initial perturbations to a laminar state with the smallest initial perturbation energy E₀ = E_c that ultimately trigger the transition to turbulence. In unstratified plane Couette flow, Rabin, Caulfield & Kerswell (J. Fluid Mech. 2012 712) identified both such a minimal seed, and other "nonlinear optimal perturbations"(NLOPS) with E₀ < E_c which maximised the gain in kinetic energy over some finite time while the flow still remained laminar. We use the same variational method of "nonlinear adjoint looping" to identify NLOPS and minimal seeds in stably stratified plane Couette flow, where a constant (stabilising) density difference is maintained across the flow. We also identify the mechanisms through which such perturbations may transiently gain both kinetic and potential energy as the bulk Richardson number is varied, identifying how stratification changes the qualitative characteristics of the optimal perturbations.

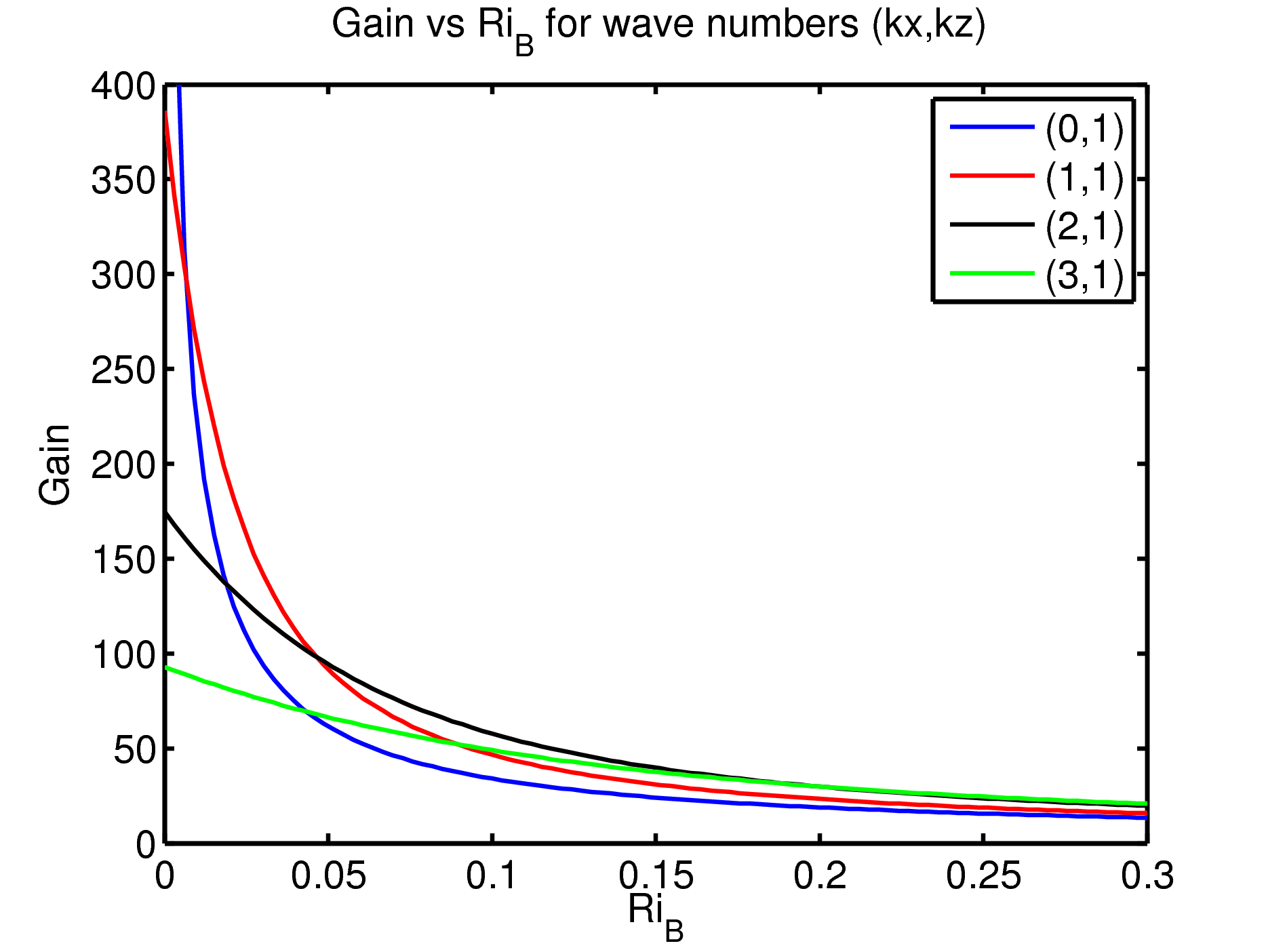
For the linear problem in which transient growth of perturbations can occur due to the nonnormality of the governing time evolution operator, we find that the possible energy gain of perturbations is rapidly reduced as the bulk Richardson number is increased. There is also a transition in the form of perturbation that is optimal for energy growth from two-dimensional, streamwise aligned vortices that primarily use the lift-up mechanism for energy growth, to three-dimensional oblique structures that primarily use the Orr mechanism for energy growth. We also find that the possibility of non-trivial transient energy growth remains for bulk Richardson numbers exceeding 0.25.

We consider the linear stability and nonlinear evolution of a Boussinesq fluid consisting of three layers with density $\rho_a + \Delta \rho/2$, $\rho_a$ and $\rho_a - \Delta \rho/2$ of equal depth $d/3$ in a 2D channel where the horizontal boundaries are driven at a constant relative velocity $\Delta U$. Unlike unstratified flow, we demonstrate that for all $Ri_b = g \Delta \rho d /(\rho_a \Delta U)^2$, and for sufficiently large $Re= \Delta U d/(4 \nu)$, this flow is linearly unstable to normal mode disturbances of the form first considered by Taylor (1931). These instabilities, associated with a coupling between Doppler-shifted internal waves on the density interfaces, have a growth rate (maximised across wavenumber and $Ri_b$) which is a non-monotonic function of $Re$. Through 2D simulation, we explore the nonlinear evolution of these primary instabilities at various $Re$, demonstrating that the primary instabilities grow to finite amplitude as vortices in the intermediate fluid layer before rapidly breaking down, modifying the mean flow to become susceptible to strong and long-lived secondary instabilities of Holmboe (1962) type, associated with vortices now localised in the top and bottom layers.

The stability and mixing of stratified shear layers is a canonical problem in fluid dynamics with relevance to flows in the ocean and atmosphere. The Miles-Howard theorem states that a necessary condition for normal-mode instability in parallel, inviscid, steady stratified shear flows is that the gradient Richardson number, $Ri_g$ is less than 1/4 somewhere in the flow. However, substantial transient growth of non-normal modes may be possible at finite times even when $Ri_g>1/4$ everywhere in the flow. We have calculated the `optimal perturbations ' associated with maximum perturbation energy gain for a stably-stratified shear layer. These optimal perturbations are then used to initialize direct numerical simulations. For small but finite perturbation amplitudes, the optimal perturbations grow at the predicted linear rate initially, but then experience sufficient transient growth to become nonlinear and susceptible to secondary instabilities, which then break down into turbulence. Remarkably, this occurs even in flows for which $Ri_g>1/4$ everywhere. We will describe the nonlinear evolution of the optimal perturbations and characterize the resulting turbulence and mixing.