Research Overview
Led by Prof. Natalia Berloff, we seek to understand the fundamental principles that govern the behavior of nonequilibrium coherent physical systems. The key to understanding the universal behaviour of such systems lies in the common description obtained when particular microscopic models are reduced to order parameter equations. Universal order parameter equations written for complex matter fields are widely used to describe systems as different as Bose-Einstein condensates of ultra cold atomic gases, thermal convection, nematic liquid crystals, solid-state condensates, lasers and other nonlinear systems.
Our focus is on modelling coherent nonequilibrium systems such as Bose-Einstein condensates of excitons, polaritons, magnons, atomic gases, superfluid helium and understanding the dynamical behaviour of these systems.
Quantum Simulation with Polaritons
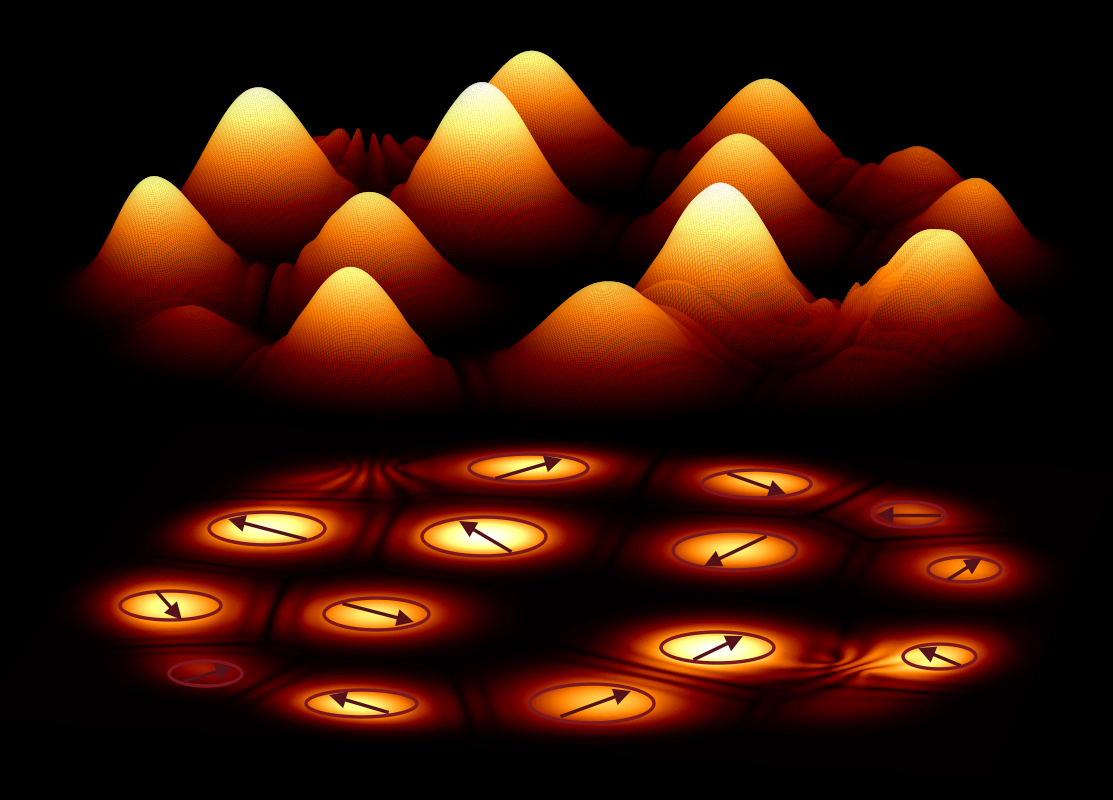
Recently we have developped a Polariton Graph Simulator, an analog simulator of hard optimization problems. The results were published in Nature Materials (press release issued by Cambridge University). The polariton graph simulator is a novel platform for solving hard optimization problems that can be mapped into the XY model. Polariton condensates can be imprinted into any two-dimensional graph by spatial modulation of the pumping laser. By controlling the pumping intensity and profile, the graph geometry and the separation distance between the lattice sites one can control the couplings between the sites and realise various phase configurations that minimize the XY model. This gives rise to the use of the polariton graph as an analogue XY Hamiltonian simulator. The search for the global minimum of the XY Hamiltonian is via a bottom-up approach which has an advantage over classical or quantum annealing techniques, where the global ground state is reached through either a transition over metastable excited states or via tunnelling between the states in time that depends on the size of the system.
We are currently continuing to develop a theoretical understanding of polariton condensate graphs, in the context of XY simulation and beyond. Recent examples have been a proposed extension to the quantum simulator platform for the simulation of Potts spin models [Kalinin and Berloff, PRL 121 (23), 235302, 2018], and the development of a theoretical framework with which polaritonic graphs may be mapped to and understood as many well known classes of nonlinear coupled oscillator networks [Kalinin and Berloff, arXiv:1902.09142, 2019].

Quantum Hydrodynamics
Quantum fluids have been studied experimentally for many years and have by now become a major focus of cryogenic physics. Applications of the subject are wide-ranging, from engineering (where, for instance, helium is used as a coolant for superconducting magnets and infrared detectors) to astrophysics (where it is invoked to explain glitches in the rotation of neutron stars). Superfluid turbulence may also provide insights into classical fluid turbulence, especially at high Reynolds numbers, where the vorticity has an intermittent, fractal character. Even though the superfluid is inviscid, there are significant differences between classical turbulence at large Reynolds number and superfluid turbulence. The most significant is that vorticity is continuously distributed in a classical (Navier-Stokes) fluid, but is quantised in a superfluid in units of h/M, where M is the mass of the boson. Turbulence in the superfluid therefore resembles a tangle of vortex filaments, whose dynamics differs from that of the chaotic but continuous vorticity of classical turbulence. We are interested in modelling, developing analytical approaches (asymptotic and perturbation methods) and applying numerical simulations in order to elucidate motions in Bose-Einstein condensates and superfluid helium. One direction of our research is to relate and improve different mathematical models of superfluid turbulence by developing hierarchies of new stochastic models of vortex motion and turbulence. Mathematical models of superfluidity and superfluid turbulence have used four approaches: (1) the phenomenological Landau two-fluid model, (2) the phenomenological Hall-Vinen-Bekherevich-Khalatnikov (HVBK) model, (3) classical inviscid model of vortex motion with ad hoc reconnections, and (4) the Gross-Pitaevskii (GP) semi-classical model. The first of these was designed to describe the superfluid motion at all temperatures at which superfluidity exists. It requires modification when the vorticity is present. The HVBK model is intended for situations in which superfluid lines are dense. The GP model is applicable at very low temperatures where normal fluid is absent; it has proved its worth especially recently in describing dilute condensates.
Although our group has been involved in the development of theories regarding a variety of systems, our hydrodynamical research is currently focused mostly on exciton polariton condensates. These are inherently nonequibriated, highly nonlinear Bose-Einstein condensates of light-matter quasiparticles. The nonequilibrium nature of these systems allows us to probe new quantum hydrodynamical regimes, to find and study new phenomena as well as to allow for greater understanding of the transition between equilibrium and nonequibrium dynamics. Some examples of work along these lines are the theory of the spontaneous formation of rotating vortex lattices [Keeling and Berloff, PRL 100, 250401, 2008], and the theory of breathing dark ring solitons in polariton condensates [Alperin and Berloff, arXiv:1905.11042, 2019].


