| Department of Applied Mathematics and Theoretical Physics |
Polariton Graph Simulator (Optimiser): an analogue Hamiltonian simulator
Popular description
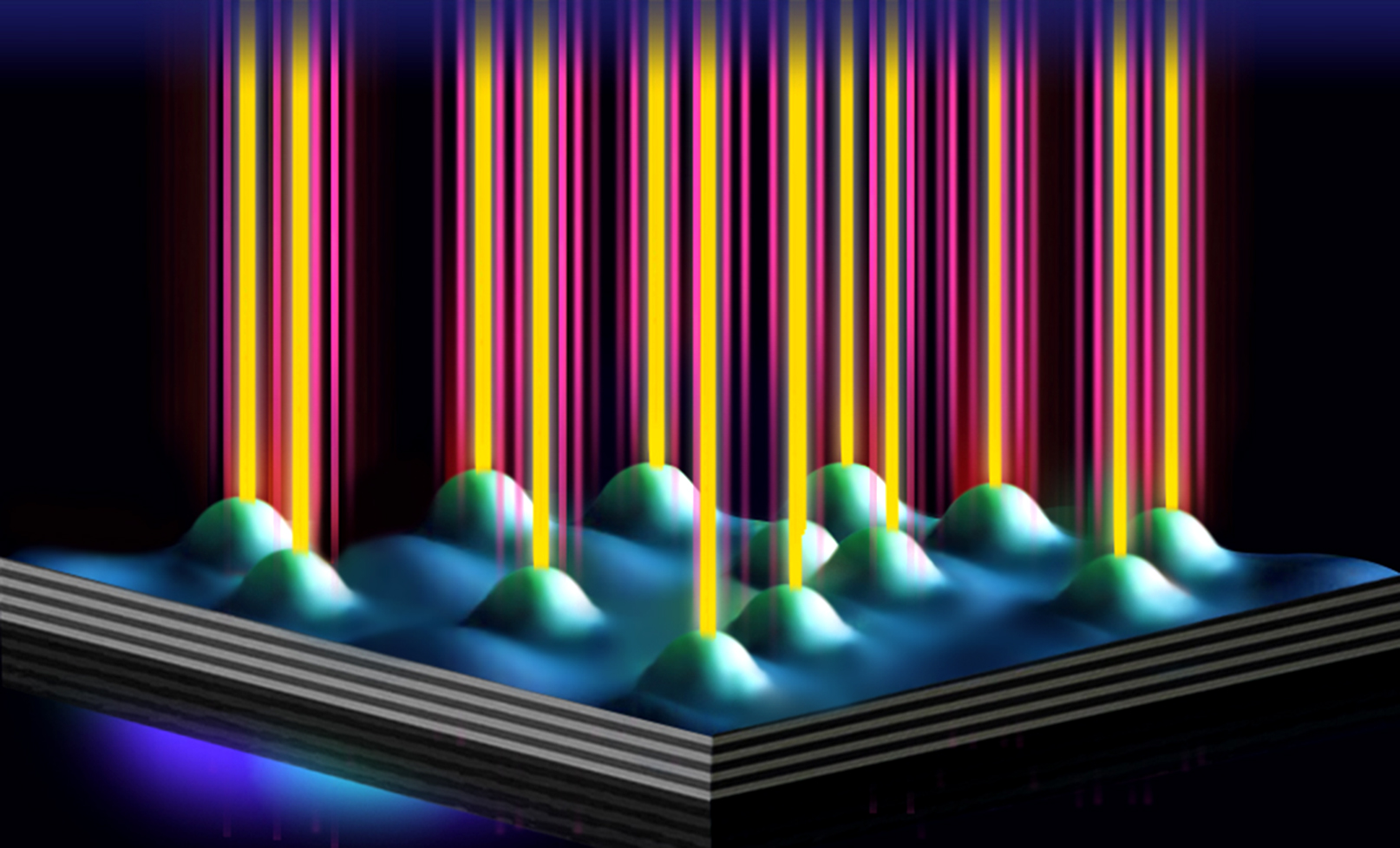
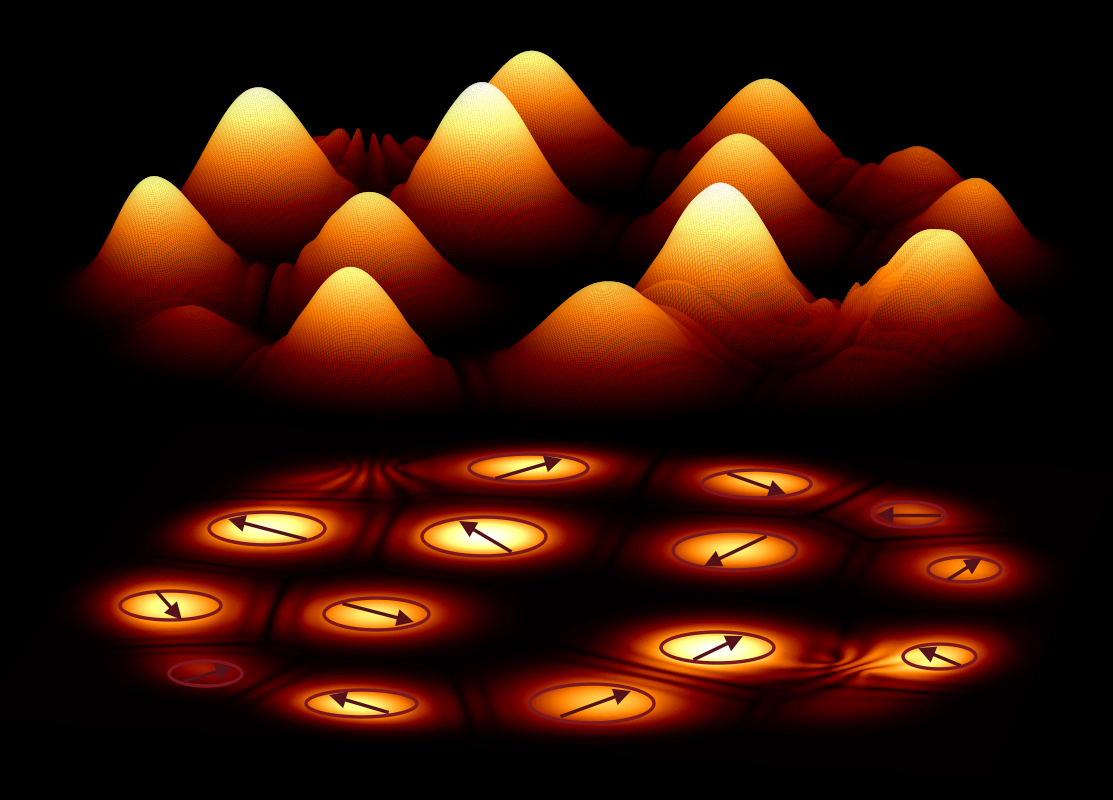 The search for an optimal solution is analogous to looking for the lowest point in a mountainous terrain with many valleys, trenches, and drops. A hiker may go downhill and think that they have reached the lowest point of the entire landscape, but there may be a deeper drop just behind the next mountain. Such a search may seem daunting in natural terrain, but imagine its complexity in high-dimensional space! This is exactly the problem to tackle when the objective function to minimise represents a real-life problem with many unknowns, parameters, and constraints.
The search for an optimal solution is analogous to looking for the lowest point in a mountainous terrain with many valleys, trenches, and drops. A hiker may go downhill and think that they have reached the lowest point of the entire landscape, but there may be a deeper drop just behind the next mountain. Such a search may seem daunting in natural terrain, but imagine its complexity in high-dimensional space! This is exactly the problem to tackle when the objective function to minimise represents a real-life problem with many unknowns, parameters, and constraints.
Modern supercomputers can only deal with a small subset of such problems when the dimension of the function to be minimised is small or when the underlying structure of the problem allows it to find the optimal solution quickly even for a function of large dimensionality. Even a hypothetical quantum computer, if realised, offers at best the quadratic speed-up for the “brute-force” search for the global minimum. What if instead of moving along the mountainous terrain in search of the lowest point, one fills the landscape with a magical dust that only shines at the deepest level, becoming an easily detectible marker of the solution? Our "magic dust" is created by shining a laser at stacked layers of selected atoms such as gallium, arsenic, indium, and aluminium. The electrons in these layers absorb and emit light of a specific colour. Polaritons are ten thousand times lighter than electrons and may achieve sufficient densities to form a new state of matter known as a Bose-Einstein condensate, where the quantum phases of polaritons synchronise and create a single macroscopic quantum object that can be detected through photoluminescence measurements. But how to create a potential landscape that corresponds to the function to be minimised and to force polaritons to condense at its lowest point? To do this, we focused on a particular type of optimisation problem, but a type that is general enough so that any other hard problem can be related to it, namely minimisation of the XY model which is one of the most fundamental models of statistical mechanics. We have shown that we can create polaritons at vertices of an arbitrary graph: as polaritons condense, the quantum phases of polaritons arrange themselves in a configuration that correspond to the absolute minimum of the objective function. XY Model is a universal classical spin model alongside other universal spin models such as an Ising and Heisenberg models. They are characterised by the given degrees of freedom, ``spins", by their interactions, ``couplings," and by the associated cost function, ``Hamiltonian". Various physical platforms have been proposed to simulate such models using superconducting qubits, optical lattices, coupled lasers etc. We introduced polariton graphs as a new platform for finding the global minimum of classical XY Hamiltonians in a variety of geometries and coupling strengths. This systems is based on well-established semiconductor and optical control technologies and benefit from flexible tunability and easy readability. Polariton condensates can be imprinted into any two-dimensional graph by spatial modulation of the pumping laser offering straightforward scalability. Polariton simulators have the potential to reach the global minimum of the XY Hamiltonian in a bottom-up approach by gradually increasing excitation density to threshold. This is an advantage over classical or quantum annealing techniques, where the global ground state is reached through transitions over metastable excited states with an increase of the cost of the search with the size of the system.
Popular PressFrequently Asked Questions
1. Why do you refer to a polariton graph simulator as “quantum”?As we discussed in NJP (2017) paper “the word ”quantum” could be attached to our proposal for a simulator to reflect the statistical nature of polariton condensates. The process of Bose-Einstein condensation is inherent to quantum statistics where a large fraction of bosons occupies the lowest quantum state, at which point macroscopic quantum phenomena become apparent. The use of the classical mean-field equations to describe the kinetics of the condensate does not negate the quantum statistic nature of its existence. At the same time, the proposed simulator has a quantum speed-up which is associated with the stimulated process of condensation i.e. an accelerated relaxation to the global ground quantum state.” 2. Polariton Graph Simulator simulates the classical XY Model. Does this mean that it can not address various aspects of quantum systems?There is an understandable misconception that classical systems cannot be used to address various aspects of quantum systems. In fact there are many classical tools that are routinely used to address quantum systems, such as numerical simulations, tensor network theory, density functional theory, and quantum Monte Carlo algorithms. The theoretical threshold between classical and quantum simulations underlines the fundamental but non-trivial and often contentious questions about quantum versus classical simulators. This discussion has recently been held within the community. We would follow the account given in several recent publications on this topic quoting specifically that of Johnson, Clark and Jaksch “What is a quantum simulator?” EPJ Quantum Technology 2014, 1:10. According to their account a device is classified as “quantum” if preparing the state relies on quantum effects: “our assignment of the quantum in quantum simulator based only on the device avoids the assumption that only simulating quantum models is hard enough to potentially benefit from a quantum device. This is not so: finding the ground state of even a classical Ising model is NP-hard and thus thought to be inefficient on both a classical and quantum device [Barahona, F.: On the computational complexity of ising spin glass models. Journal of Physics A: Mathematical and General 15, 3241 (1982) and Bernstein, E., Vazirani, U.: Quantum complexity theory. SIAM J on Computing 26, 1411–1473 (1997)].” According to this definition our polariton simulator can be classified as “quantum”, since the process of the condensation that guarantees the achievement of the global minimum of the classical XY Hamiltonian is the property of quantum statistics, namely Bose-Einstein condensation. |