Harvey Reall: Research
This (incomplete!) summary is roughly chronological. If you want to see what I've been working on recently then scroll to the bottom.
Click here for a list of all of my papers.
If you would like to study for a Ph.D under my supervision then please read this guidance.
Black rings
The study of General Relativity (GR) with extra dimensions is motivated by string theory, especially via the AdS/CFT correspondence.
In four spacetime dimensions, theorems proved in the 1970s establish that black holes are always topologically spherical and, in equilibrium, any vacuum black hole is described by the Kerr solution of the Einstein equation. The Kerr solution is uniquely specified by its mass and angular momentum so, in equilibrium, a four-dimensional black hole is fully characterized by just these two numbers.
Surprisingly, these properties do not hold in higher dimensions. Roberto Emparan and I found a solution of the five-dimensional vacuum Einstein equation describing a rotating black hole with the topology of a donut, or ring. We called these objects "black rings". These are the first examples of topologically non-spherical black holes. The existence of black rings also shows that higher dimensional black holes are not uniquely characterized by mass and angular momentum.
See here for a non-technical description of this work and here for a review article on higher dimensional black holes.
Supergravity solutions
The low energy limit of superstring theory is supergravity theory, an extension of GR. A special class of solutions of supergravity are the so-called supersymmetric solutions. This is because sometimes one can calculate exactly properties of such solutions using the microscopic string theory. An important example of this is the string theory calculation of black hole entropy, which was first done for supersymmetric black holes in five dimensions. Following the discovery of black rings, one can ask whether supersymmetric black rings might also exist. This question was part of the motivation for a paper I wrote with Jerome Gauntlett, Jan Gutowski, Chris Hull, and Stathis Pakis in which we carried out a full classification of all supersymmetric solutions of minimal 5d supergravity, the first such classification achieved for a higher-dimensional theory. Henriette Elvang, Roberto Emparan, David Mateos and I exploited this classification to discover the first supersymmetric black ring solutions. It is still not fully understood how to calculate the entropy of these solutions in string theory.
In AdS/CFT one would like to use CFT to calculate the entropy of anti-de Sitter (AdS) black holes. However, since the CFT is strongly coupled this is difficult. But if the black hole is supersymmetric then one may be able to overcome this problem. So it is of interest to find supersymmetric AdS black hole solutions. The first examples of supersymmetric black holes in 5d AdS (dual to a 4d CFT) were constructed by Jan Gutowski and myself. These were later generalized in a paper I wrote with James Lucietti and Hari Kunduri.
Near-horizon geometries
The existence of black rings, and evidence for many other types of higher dimensional black holes, reveals that higher dimensional black holes are considerably more complicated than 4d ones. How can one try to classify such black holes? A simplifying assumption is that the black hole is extremal, i.e., has the minimum mass compatible with its angular momentum and any other charges. Supersymmetric black holes are always extremal, so extremal black holes play an important role in string theory.
Such a black hole admits a "near-horizon limit" in which one zooms in on the event horizon, and the geometry becomes more symmetrical. I introduced the use of near-horizon geometries as a method for classifying extremal black holes in my classification of supersymmetric near-horizon geometries of 5d supergravity. Together with Kunduri and Lucietti, I proved that a near-horizon geometry always exhibits an enhancement of symmetry associated with a 2d AdS spacetime.
Black hole stability
A natural question about black rings (and other higher dimensional black holes) is: are they stable? In four dimensions, it is believed that the Kerr solution is stable (at least if non-extremal). But it turns out that the higher-dimensional analogues of Kerr can be unstable if they rotate too rapidly. See here for a paper I wrote with Oscar Dias, Pau Figueras, Ricardo Monteiro and Jorge Santos providing the first demonstration that small perturbations of such black holes can grow exponentially with time.
Turning to black rings, Keiju Murata, Pau Figueras and I showed that "fat" black rings exhibit an axisymmetric instability. It was shown later that a non-axisymmetric instability afflicts "thin" rings so the known vacuum black ring solutions are all unstable. The evolution of the instability has been studied in supercomputer simulations.
In 4d, non-extremal (asymptotically flat) black holes are classically stable: when perturbed, the perturbation decays. Suprisingly Stefanos Aretakis (as part of his Cambridge Ph.D) discovered that extremal black holes suffer from a subtle instability. He showed that a scalar field in an extremal Kerr or Reissner-Nordstrom black hole spacetime has the property that its gradient does not decay along the event horizon of the black hole. Second, or higher derivatives of the scalar field grow with time on the event horizon although they decay outside the black hole. James Lucietti and I showed that this instability also occurs for gravitational perturbations of an extremal Kerr black hole.
What happens to the Aretakis instability when one includes the effects of the gravitational backreaction of the perturbation? I investigated this in a paper with Keiju Murata and Norihiro Tanahashi. We showed that the instability is still present but generically it is a transient effect. However, we showed that the initial perturbation can be fine-tuned so that the black hole remains extremal. In such spacetimes, there is a nonlinear version of the Aretakis instability, which never ends.
The blow-up of higher derivatives along the event horizon suggests that higher derivative corrections to the equations of motion (e.g. arising from string theory) might become important at the horizon, indicating a breakdown of effective field theory. Shahar Hadar and I showed that this does not happen: general covariance ensures that growing terms are always multiplied by decaying ones so higher derivative terms remain small.
Well-posedness of modified gravity
There has been a lot of interest in exploring alternatives to General Relativity, i.e., "modified gravity". Some cosmologists hope that such theories may explain the observed accelerated expansion of the Universe without invoking a cosmological constant. People working on gravitational waves would like to explore theories that differ from GR in the strong field regime, to see what kind of deviation might be observable with gravitational wave detectors. But are theories of modified gravity mathematically self-consistent?
A basic requirement of a classical theory is that the initial value problem should be well-posed. This means that, given initial data, there should exist a unique solution of the equations of motion, and this solution should depend continuously on the initial data. Well-posedness is essential for solving the equations of motion numerically on a computer. GR is a theory with a well-posed initial value problem. I am interested in whether this is also true for theories of modified gravity. Establishing well-posedness involves finding a "good gauge" for theory, and a good way of "gauge fixing".
A popular class of modified gravity theories are the Horndeski theories. These are the most general diffeomorphism invariant theories of a metric tensor coupled to a scalar field. In this paper, my student Giuseppe Papallo and showed that the standard way (so-called harmonic gauge) of establishing well-posedness in GR does not extend to Horndeski theories, even when the deviation from GR is small. However, in subsequent work, Aron Kovacs and I we were able to find a formulation of these theories that does admit a well-posed initial value problem, at least for small deviations from GR. This formulation should be suitable for performing numerical simuluations of black hole mergers in these theories, and thereby learning about the nature of possible deviations from GR for strong gravitational fields.
You can watch me give a talk on this work here.
Superluminal wave equations
This concerns classical field theories in Minkowski spacetime. Some theories allow superluminal propagation of signals around non-trivial backgrounds. It is sometimes claimed that such theories suffer from "causality violation" or admit "time machine" solutions. Determining whether or not this claim is true was the motivation for this paper that I wrote with Felicity Eperon (my student) and Jan Sbierski. A violation of casuality would be problematic because it implies a breakdown in predictability. So rather than focusing on causality, we investigated predictability, specifically: what is the largest region of spacetime in which a solution of the theory is uniquely determined by initial data? Such a region must be a "globally hyperbolic development" of the initial data. One might think that the largest such region should be a maximal globally hyperbolic development (MGHD). So maybe MGHDs would exhibit some pathological behaviour in superluminal theories that is not present for subluminal theories. For example, "formation of a time machine" would require that the solution can be extended in a (non-unique) way beyond the MGHD so perhaps this could happen in a superluminal theory but not in a subluminal one.
Surprisingly, we found a more basic difference between superluminal and subluminal theories. We showed that in a superluminal theory one always has a unique MGHD of the initial data. However in a generic subluminal theory, MGHDs are not always unique. This means that, if one has a solution of a subluminal theory, there may be no simple way of determining the region of spacetime in which this solution is uniquely determined by the initial data. In this sense, superluminal theories are more predictive than generic subluminal ones!
Strong cosmic censorship
Is the future predictable from initial data? In GR this is subtle: this is the subject of the strong cosmic censorship conjecture. The conjecture says that, for some suitable class of initial data for Einstein's equation, generically time evolution does not lead to the formation of a region of spacetime which cannot be predicted from the initial data. Charged or rotating black holes appear to violate this conjecture because they contain an inner horizon beyond which one cannot determine spacetime from the initial data. But there is good evidence that such inner horizons are unstable and so will not form dynamically.
Most studies of this instability have neglected the cosmological constant because it is tiny on the scales relevant to black holes. But recent work, which I reviewed here, indicates that the instability may be absent if the cosmological constant is positive, as is the case in our Universe. Motivated by this work, Oscar Dias, Jorge Santos and I studied gravitational and electromagnetic perturbations of charged black holes with positive cosmological constant. We found that the inner horizon of such black holes can be very stable if the black hole is highly charged and sufficiently large, so strong cosmic censorship is badly violated in Einstein-Maxwell theory with positive cosmological constant. However, in this paper (with Felicity Eperon), we showed that the conjecture is respected in the more physical case of (uncharged) rotating black hole solutions.
We have also investigated strong cosmic censorship for the BTZ black hole. This is a rotating black hole in 2+1 dimensions with negative cosmological constant. In this paper we showed that the inner horizon of such a black hole can be stable if the hole rotates sufficiently rapidly. So this is another example for which strong cosmic censorship is violated. This raises the question of whether quantum effects might rescue the conjecture. We showed that the energy-momentum tensor of a quantum field can diverge at the inner horizon but this does not happen for a rapidly rotating hole. So vacuum polarization does not enfore strong cosmic censorship.
Watch me give a talk about this work here.
Second law of black hole mechanics
In General Relativity, black holes are governed by a set of laws analogous to the laws of thermodynamics. Hawking's discovery of black hole radiation revealed that this is more than an analogy: black holes really are thermodynamics objects. In the 1990s, Wald showed that a first law of black hole mechanics holds for any theory of gravity arising from a diffeomorphism invariant Lagrangian. In particular, this work provides a notion of entropy (the Wald entropy) for a black hole in such a theory.
What about the second law? Work of Aron Wall explained how to extend the Wald entropy to obtain a definition of entropy that satisfies the second law for linear perturbations of a time-independent black hole. In work with Stefan Hollands and Aron Kovacs, we showed how to go beyond linear perturbations and obtain a definition of entropy that satisfies the second law to quadratic order in perturbation theory provided one treats higher derivative terms in the sense of effective field theory.
Watch me give a talk about this work here.
In subsequent work with Iain Davies we showed that this definition can be improved to obtain a definition of black hole entropy that satisfies a second law non-perturbatively.
Creases, corners and caustics
Even in a smooth spacetime, the event horizon of a dynamical black hole is usually not a smooth surface. Typically it fails to be smooth at points where light rays enter the horizon: "past endpoints of horizon generators". Endpoints arise when a black hole is formed in gravitational collapse, and also in a black hole merger. In this paper, Maxime Gadioux and I studied the properties of such past endpoints, classifying them as crease points (end points of exactly 2 generators), corner points (end points of exactly 3 generators) and caustic points (where infinitesimally nearby generators intersect). At an instant of time, crease points form lines (creases) on the horizon and corner points look like a vertex of a tetrahedron or cube. In spacetime, the crease points form a 2d surface: the "crease submanifold". If one foliates spacetime by surfaces of constant time then there will be special surfaces which are tangent to this submanifold. These describe instants of time in which the horizon undergoes a qualitative change. We classified such changes. This classification includes the important example of a black hole merger: our work provides an exact local description of the event horizon near the merger point. This is shown in the image below where time increases from left to right, the green lines are creases, and the other colours indicate generators entering the horizon.
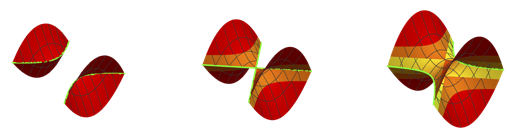
Watch me give a talk about this work here.
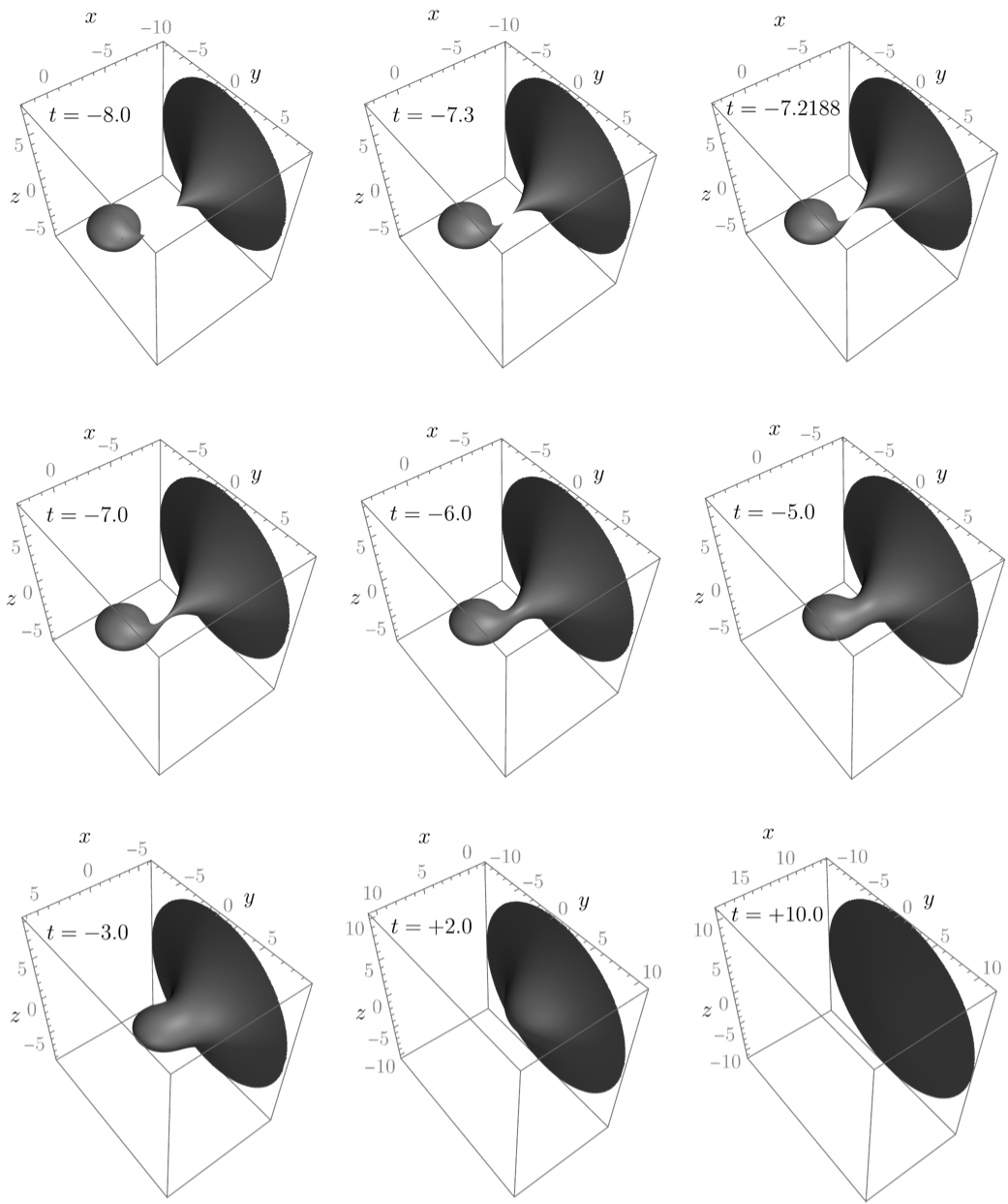
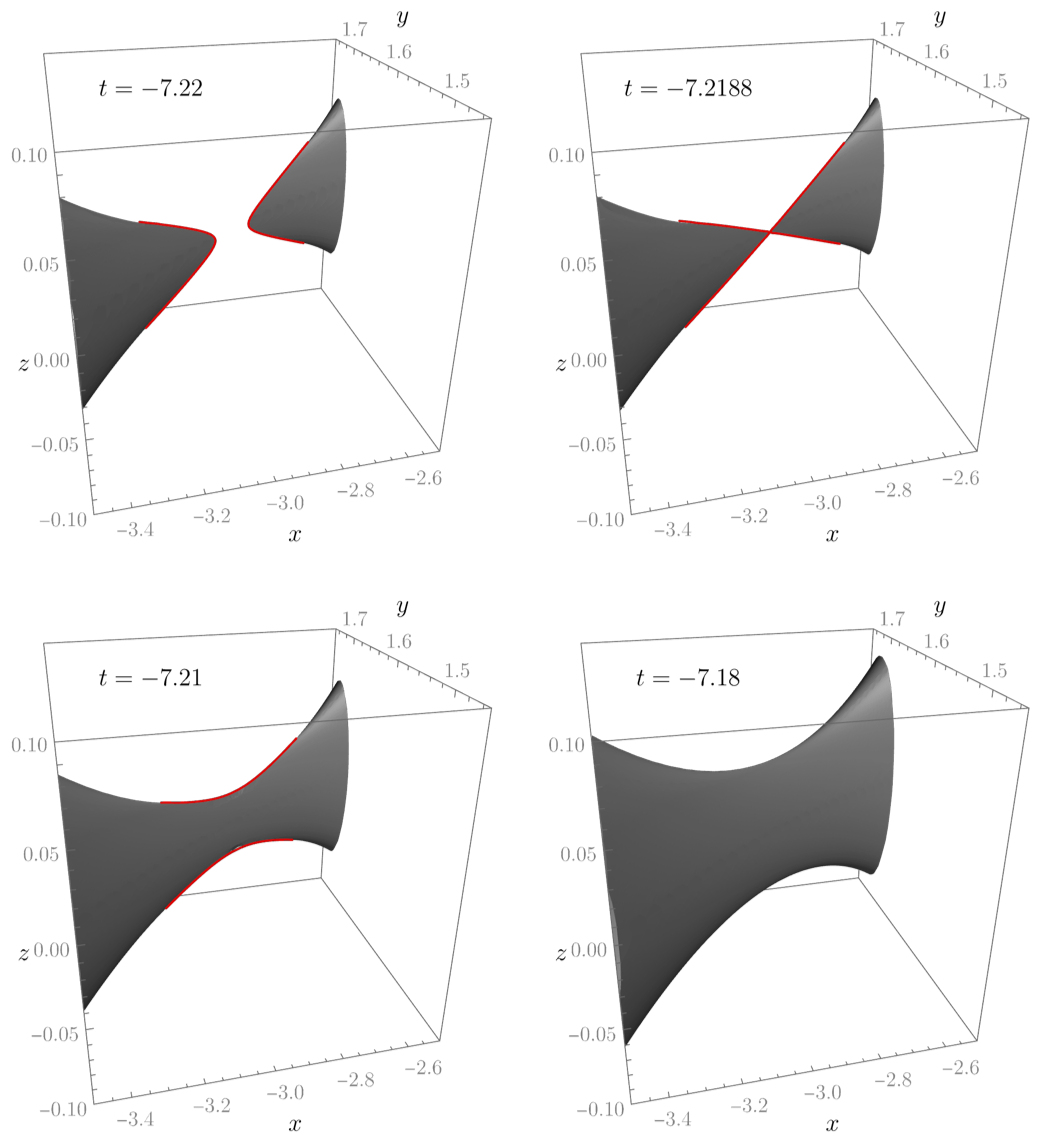
In a follow up to this work, Maxime Gadioux, Robie Hennigar and I studied the structure of the event horizon in a merger of a small rotating (Kerr) black hole with a much larger black hole. Here are some pictures showing this behaviour. The first set of images shows the small black hole approaching part of the large black hole horizon, with the event horizon plotted for nine different instants of time. Near to the "instant of merger", both horizons develop a spiky feature and the merger appears to involve a merger of these spikes. The second set of images is a zoom-in on the behaviour near the "instant of merger'': the spikes are resolved into chisel-like features, with creases (the red lines) along their sharp edges. The merger is revealed to be a merger of creases, exactly as predicted by my earlier work with Maxime.
Third law of black hole mechanics
A black hole with a given mass has an upper bound on its spin or charge. A hole with the maximum possible spin or charge is called extremal. The third law of black hole mechanics states that it is impossible for a non-extremal black hole to become extremal in finite time in classical General Relativity. A proof of this law was presented in the 1980s but this turned out to be incorrect: it has been proved that a massless charged scalar field can undergo gravitational collapse to form an exactly extremal black hole, with an intermediate period in which it is non-extremal. This process involves matter with a very large charge to mass ratio. What happens if the charge to mass ratio of matter is bounded? In this paper, I proved that one cannot form a maximally charged black hole in gravitational collapse if the charge to mass ratio of matter is less than one (in geometric units). More generally, one cannot form a supersymmetric black hole in gravitational collapse. Thus the third law holds for such black holes. The proof makes use of spinorial methods first used in the proof of the positive energy theorem in General Relativity. A follow up paper with Aidan McSharry presented some generalisations of this work.