Linear Multistep Methods (LMMs) and A-stability
Contents
Introduction
Note: Since all multistep methods considered in the course are linear, the course notes speak of 'multistep methods' instead of 'linear multistep methods'. Hopefully this should cause no confusion.
This GUI aims to demonstrate and contrast:
- the root condition for LMMs
- A-stability for more general methods including LMMs.
We consider a general LMM of the form
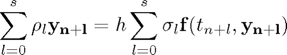
(where 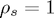 and
and 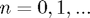 )
)
Theory
The role of the root condition for LMMs is covered in the course notes in 5.3.2 The convergence of multistep methods.
Quick review: we consider the roots of the polynomial 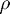 with coefficients
with coefficients 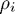 : the root condition is obeyed if these lie within the closed unit disc and all roots on the boundary are simple. By the Dahlquist Equivalence Theorem, a method of order
: the root condition is obeyed if these lie within the closed unit disc and all roots on the boundary are simple. By the Dahlquist Equivalence Theorem, a method of order 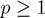 is convergent iff
is convergent iff 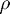 satisfies the root condition.
satisfies the root condition.
The role of A-stability is covered in the course notes in "6.2 Linear stability".
Quick review: it is desirable for the numerical solution produced by a method to tend to zero if the exact solution does. It turns out that for linear problems it is enough to consider the solution of the simple scalar equation 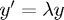 with fixed step-size
with fixed step-size 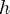 . Whether the numerical solution tends to zero will be a function of
. Whether the numerical solution tends to zero will be a function of 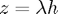 . The region where this does occur is called the linear stability domain. If the linear stability domain contains all complex numbers with negative real part, then we say that the method in question is A-stable.
. The region where this does occur is called the linear stability domain. If the linear stability domain contains all complex numbers with negative real part, then we say that the method in question is A-stable.
We restrict our attention to the linear stability domain of LMMs and a certain class of one-step methods.
For LMMs the linear stability domain has a boundary that can be written in a simple fashion in terms of the coefficient polynomials of the method (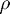 and
and 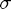 ).
).
For many one-step methods, we will typically be able to write
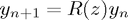
where 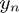 is the numerical solution of
is the numerical solution of 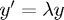 with fixed step-size
with fixed step-size 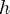 . In this case the function
. In this case the function 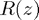 tells us everything we need to know about the linear stability domain:
tells us everything we need to know about the linear stability domain:  as
as  iff
iff 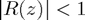 .
.
More details about how the plotting is done can be found in [1] - Section 7.6 starting on page 262
The GUI
stability_gui
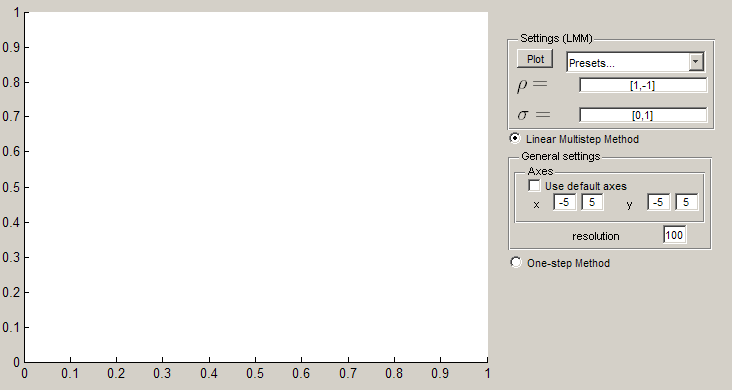
The Plot
The plot displays the linear stability domain of a method (shaded in blue with black boundary). A black dashed line marks the imaginary axis.
For LMMs the unit circle is also plotted (dashed magenta curve), and the roots of the polynomial 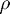 are plotted as empty red points. The root condition may then be inspected by eye (but beware of repeated roots).
are plotted as empty red points. The root condition may then be inspected by eye (but beware of repeated roots).
Controls
To switch between the LMM and one-step modes, use the radio buttons in the bottom centre of the GUI. The maximum range covered by the plot can also be set using the controls just below. The 'resolution' control determines how many points are used to produce the plot - increase this if the curves are jagged and decrease it if plotting takes an excessive amount of time.
Specifying methods
LMMs are entered by specifying their coefficients (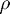 and
and 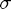 ) as row vectors.
) as row vectors.
One-step methods are entered by specifying 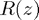 .
.
In either case, there are preset methods that can be selected using the drop-down box above the entry fields.
LMM Presets
- BDF1 to BDF 6 are the BDF methods of orders 1 through 6 (see notes 5.3.5 BDF methods).
- AB1 to AB5 are the Adams-Bashforth methods of orders 1 through 5 (see notes 5.3.4 Adams Methods).
- AM0 to AM4 are the Adams-Moulton methods of orders 1 through 5 (see notes 5.3.4 Adams Methods).
One-step Presets
- RK2E is an explicit two-stage Runge-Kutta method (order two). All explicit RK methods of a given order have the same
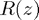 .
. - RK2I is the two-stage implicit Runge-Kutta method (order three) described in Stiffness and Runge-Kutta in 6.3 Overcoming the Dahlquist barrier
- GL2 is the two-stage implicit Gauss-Legendre method (order four) described in the example in 6.3 Overcoming the Dahlquist barrier
Code
- stability_gui.m (Run this)
- stability_gui.fig (Required)
All files as .zip archive: a_stability_all.zip
References
[1] Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems by Randall J. LeVeque [SIAM, Philadelphia, 2007]

