From Polynomial Interpolation to Cryptography
Some extensions to the material in lectures on polynomial interpolation including example sheets and beyond.
Contents
Introduction
In lectures you've seen polynomial interpolation from (essentially) one point of view. In what follows, it is helpful to cast polynomial interpolation in the framework of matrices and linear equations.
In standard polynomial interpolation of the function 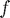 we seek coefficients
we seek coefficients 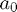 ,
, 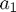 , ...
, ... 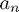 for the polynomial
for the polynomial 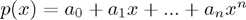 such that for some set of pairwise distinct real numbers
such that for some set of pairwise distinct real numbers 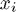 ,
, 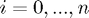 the conditions
the conditions
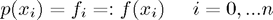
hold.
Interpolation in the style of Vectors and Matrices
The above conditions can be written as a set of 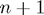 linear equations in the
linear equations in the 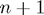 unknowns
unknowns 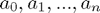 ; we can write this in matrix form:
; we can write this in matrix form:
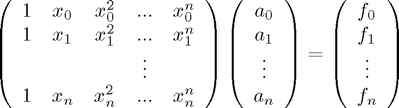
The matrix on the LHS has a form that occurs so frequently that it is given a special name: it is a Vandermonde matrix.
It can be shown that because the 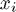 are pairwise distinct the determinant of the matrix is nonzero, hence we get a unique solution to the interpolation problem. No surprises here, this was proved (from a different point of view) in lectures!
are pairwise distinct the determinant of the matrix is nonzero, hence we get a unique solution to the interpolation problem. No surprises here, this was proved (from a different point of view) in lectures!
In principle, once we have formulated the matrix form for a (well-posed) interpolation problem, we simply have to apply standard methods to solve the linear system of equations. In MATLAB this is especially easy to do:
B=[1 -1 1; 1 0 0; 1 1 1;]; f=[0; 1; 0;]; a=B\f; display(a);
a =
1
0
-1
(This interpolates the values 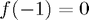 ,
, 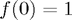 and
and 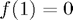 - the result corresponds to the polynomial
- the result corresponds to the polynomial 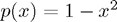 )
)
CAUTION!
- There may be less general (but more efficient) approaches.
- Different ways of phrasing the problem may lead to different ('better') matrices. For example, if we use the Newton form of the interpolating polynomial the matrix becomes upper triangular (although it is no longer Vandermonde) - try this.
Higher-order ('Osculatory') Interpolation (cf. Example Sheet 1)
As on Example Sheet 1, we may be required to interpolate the derivative of the function 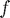 at some point, as well as the function value itself. Suppose this point is
at some point, as well as the function value itself. Suppose this point is 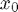 and that we no longer interpolate
and that we no longer interpolate 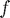 at
at 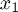 . Then we have:
. Then we have:
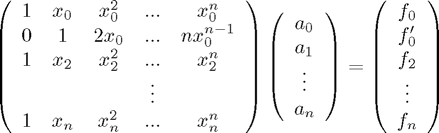
Can you see where the new second row comes from? The condition
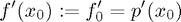
is, more explicitly
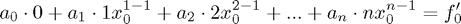
It is not hard to see how this can be extended further to higher-order derivatives and more points, or even to 'interpolating' features of the function 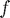 other than derivatives. But:
other than derivatives. But:
CAUTION!
- In the example above, we no longer interpolate
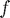 at
at 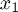 - otherwise the system becomes overdetermined!
- otherwise the system becomes overdetermined! - More generally: to obtain the right (i.e. same) number of equations and unknowns, you may have to increase the degree of the interpolating polynomial by adding more coefficients.
- The conditions you impose on the interpolating polynomial must be independent - that is, they must lead to linearly independent rows in the resulting linear system.
Extensions
We sketch below two applications of polynomial interpolation.
Richardson Extrapolation [sic!] and Romberg integration
Richardson Extrapolation is a general approach for using successive approximation values 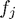 ,
, 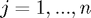 generated by some convergent scheme (e.g. root finding) to produce a new (and hopefully improved!) estimate of the limit.
generated by some convergent scheme (e.g. root finding) to produce a new (and hopefully improved!) estimate of the limit.
We interpolate 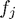 by a polynomial
by a polynomial 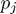 in inverse powers of
in inverse powers of 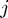 :
:
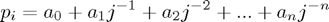
Having calculated the 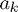 (which can be done by divided differences) we take
(which can be done by divided differences) we take 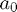 as our new estimate. The intuition is that
as our new estimate. The intuition is that  as
as 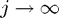 , and
, and 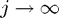 represents passing to the limit of successive approximations.
represents passing to the limit of successive approximations.
Applying this approach to numerical quadrature (with either the trapezoidal or rectangle rules) gives the method of Romberg integration; see http://en.wikipedia.org/wiki/Romberg%27s_method for more details.
Shamir's Secret-Sharing Scheme
In cryptography, this is a method for distributing a secret number among N people such that no fewer than K of them working together can reconstruct the secret number.
The details are straightforward but somewhat involved; the scheme can be understood as based on polynomial interpolation in a finite field. For more details see http://en.wikipedia.org/wiki/Shamir%27s_Secret_Sharing

