Department of Applied Mathematics and Theoretical Physics

Numerical Analysis Course

Gaussian Quadrature

This Graphical User Interface (GUI) illustrates some features of various quadrature rules for evaluating

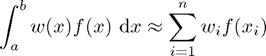
$$\int_a^b w(x) f(x)~\mathrm{d}x \approx \sum_{i=1}^n w_i f(x_i)$$

Reminder

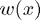  • $w(x)$ is the (rule-dependent) weight function
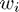  • $w_i$ are the quadrature weights
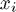  • $x_i$ are the quadrature nodes

Contents

Introduction

After saving all of the MATLAB code downloadable below, running gauss_quad_gui_run.m produces the following window:

gauss_quad_gui

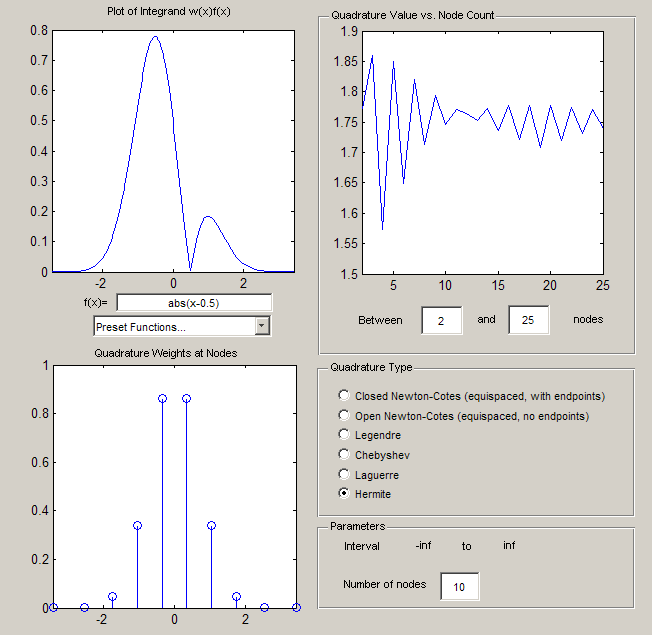
Using the GUI

The various elements of the GUI are as follows

Plot of integrand w(x)f(x) (upper left)

This is a plot of 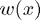$w(x)$ times the given function 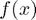$f(x)$, over the relevant (rule-dependent) interval.

The function f may be specified below the plot, either by using the text box or by selecting any of the preset functions.

NB: in MATLAB's notation, the multiplication (*), division (/), and exponentiation (^) operators MUST be preceded by a dot (.) e.g. 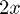$2x$ is 2.*x in MATLAB's notation.

Quadrature Value vs. Node Count (upper right)

This shows successive approximations with a varying number of nodes, specifed just below the plot. This allows visualisation of how (and indeed whether) the approximants converge.

Quadrature Weights at Nodes (lower left)

This shows the quadrature weights 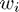$w_i$ plotted as vertical stems at the quadrature nodes 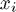$x_i$. The number 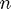$n$ of nodes/weights can be controlled with the box at the lower right part of the window.

Quadrature Type (lower right)

This selects the quadrature rule. The options are summarised in the table below. See also the lectures on Gaussian quadrature.

Name Weight Function Interval Nodes
Closed Newton-Cotes 1 [-1,1] Equally spaced, including endpoints
Open Newton-Cotes 1 [-1,1] Equally spaced, excluding endpoints
Legendre 1 [-1,1] Roots of n-th degree Legendre polynomial
Chebyshev 1/sqrt(1-x^2) [-1,1] Roots of n-th degree Chebyshev polynomial
Laguerre exp(-x) [0,infinity] Roots of n-th degree Laguerre polynomial
Hermite exp(-x^2) [-infinity,infinity] Roots of n-th degree Hermite polynomial

MATLAB Code

All files as .zip archive: gaussian_quadrature_all.zip


Published with MATLAB® 7.10