Forward Euler and gradient fields
Consider the first order ODE 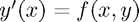 . There is a close relation between the Forward Euler (FE) method and the gradient field of the function
. There is a close relation between the Forward Euler (FE) method and the gradient field of the function 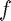 , due to the way FE discretise.
, due to the way FE discretise.
Contents
The GUI
Running the downloadable MATLAB® code on this page opens a GUI which demonstrates the relation between FE and gradient fields.
gradient_field_GUI
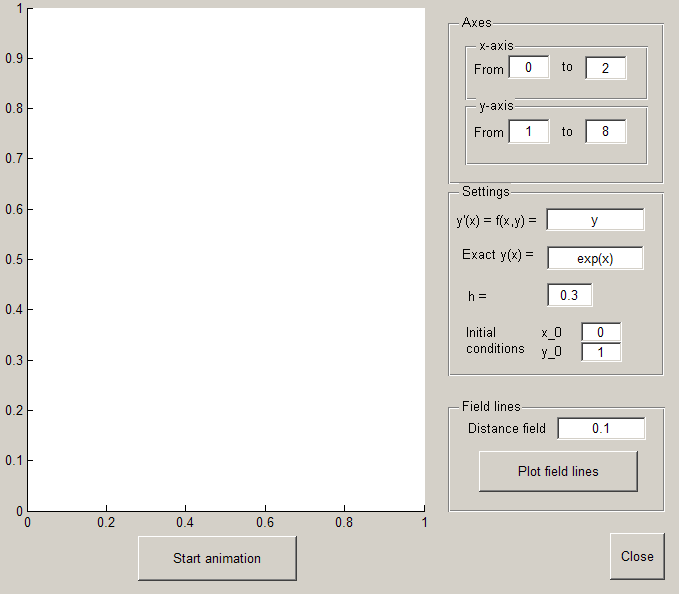
Interface
You can input the axes limits, the RHS of the ODE equation, the exact solution (if known), the time-step 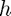 , and the initial condition
, and the initial condition 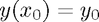 .
.
By clicking on 'Plot field lines', the field lines of the function 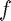 will appear. You can control the density of the field lines by changing the parameter 'Distance field lines'.
will appear. You can control the density of the field lines by changing the parameter 'Distance field lines'.
To start the animation, click on 'Start animation'. Once the animation begins, to stop it click on 'Stop animation'.
Notice that the exact solution is plotted in red, while the FE approximation is plotted in blue. You can see that the numerical error makes the FE approximation go to adjacent field lines.
Code
- gradient_field_GUI.m (Run this)
- gradient_field_GUI.fig (Required - GUI figure)
All files as .zip archive: gradient_field_all.zip

