LU Factorisation
The LU factorisation of a square matrix 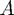 is its decomposition as the product
is its decomposition as the product 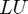 where the matrix
where the matrix 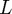 is lower triangular and the matrix
is lower triangular and the matrix 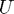 is upper triangular.
is upper triangular.
Note that the LU factorisation of a given matrix 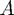 is not unique (but it can be made so by requiring, for example, that the diagonal entries of
is not unique (but it can be made so by requiring, for example, that the diagonal entries of 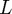 are 1).
are 1).
Not all matrices have an LU decomposition, if we do not allow pivoting. However, if the matrix is non-singular, it always has an LUP decomposition (LU with pivoting - where 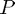 is a permutation matrix).
is a permutation matrix).
Contents
Theory
The LU factorisation without pivoting can be implemented as follows:
1. Set 
2. For all 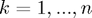 , set
, set 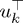 to the
to the 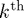 row of
row of 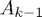 , and set
, and set 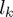 to the
to the 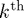 column of
column of 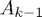 , scaled so that
, scaled so that 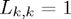 .
.
3. Set 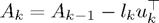 .
.
4. Increment 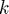 by one, and go back to step 2.
by one, and go back to step 2.
In the above, 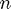 is the dimension of
is the dimension of 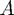 , the
, the 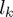 are the columns of
are the columns of 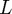 and the
and the 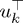 are the rows of
are the rows of 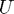 .
.
Aim
The aim of this GUI is to illustrate LU factorisation without pivoting.
The GUI
Running the downloadable MATLAB® code on this page opens a GUI which demonstrates the LU algorithm without pivoting.
IB_LU_GUI
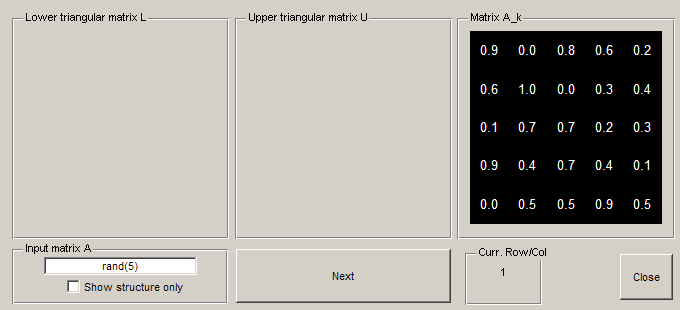
Interface
You can enter any square matrix you like. If you want to just see the structure of the matrices (black square for non-zero entries and white square for zero entries), you can click on the 'Structure only' radio button. The GUI shows by default both the structure and the values of the entries. Notice that if your matrix or its entries are large, it is advisable to switch to the 'structure only' mode. As soon as you enter a matrix, it will appear as your current 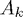 .
.
To start the LU algorithm, click on the 'Next' push button. You will see the new 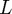 , the new
, the new 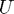 and the new
and the new 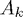 . To keep track of the current row (or equivalently column), there is a display to the right of the 'Next' push button. Keep going until the algorithm terminates (when the string 'Finished!' appears). To start a new iteration, input another matrix.
. To keep track of the current row (or equivalently column), there is a display to the right of the 'Next' push button. Keep going until the algorithm terminates (when the string 'Finished!' appears). To start a new iteration, input another matrix.
Note: if the matrix entered does not have an LU factorisation without pivoting, a warning message will appear at the problematic stage and the algorithm will stop.
Try, for example, the matrix:
[1 1 1; 1 1 2; 1 2 1];
To close the GUI, click on the 'Close' push button.
Code
- IB_LU_GUI.m (Run this)
- IB_LU_GUI.fig (Required)
All files as zip archive: lu_fac_all.zip

