Numerical Methods for First Order ODEs
Here we consider numerical methods to solve differential equations of the form
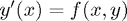
with a given intial condition 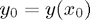 .
.
In particular, we will look at the Forward Euler, Backward Euler, Trapezoid, Runge-Kutta 4, Adam-Bashforth 2 and Heun methods.
Contents
Forward Euler
The formula is:
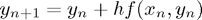
where 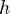 is the step-size.
is the step-size.
Backward Euler
The formula is:
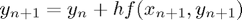
where 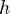 is the step-size.
is the step-size.
Trapezoidal
The formula is:
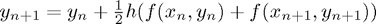
where 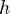 is the step-size.
is the step-size.
Runge-Kutta 4
This is the following 4th-order Runge-Kutta method:
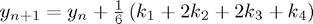
with
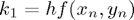 ,
,
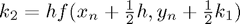 ,
,
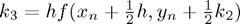 ,
,
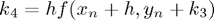 .
.
where 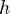 is the step-size.
is the step-size.
Adam-Bashforth 2
This is a two-step method with the following formula:
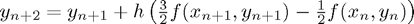
where 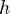 is the step-size.
is the step-size.
Heun
Heun's method has the following formula:
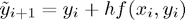
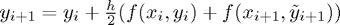 .
.
where 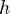 is the step-size. So in Heun's method, there is a first approximation at the intermediate value, and then the final approximation at the next integration point.
is the step-size. So in Heun's method, there is a first approximation at the intermediate value, and then the final approximation at the next integration point.
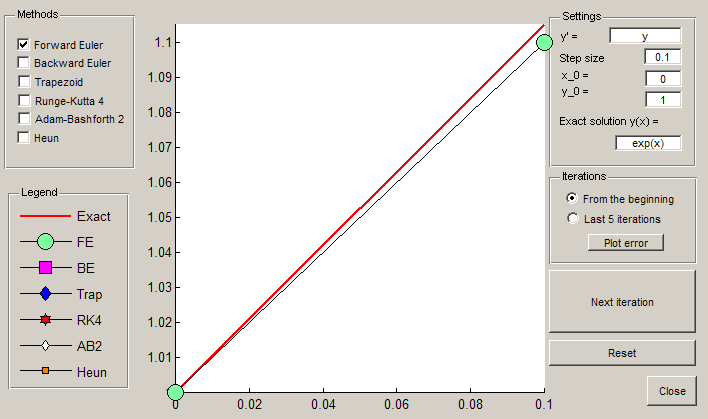
The GUI
Running the downloadable MATLAB® code on this page opens a GUI which allows you to compare different numerical methods for first order ODEs.
IB_ODE_GUI
@(x)(func(x))
The Code
- IB_ODE_GUI.m (Run this)
- IB_ODE_GUI.fig (Required)
All files as zip archive: ode_all.zip

