The Milne Device (Predictor-Corrector Methods)
The Milne Device combines two methods to more appoximate the error in each step to ensure that the solution stays within a given error tolerance.
Contents
Predictor-Corrector Pairs
We choose two different (multistep) methods with the same order. Comparing the error terms enables us to compute a first order approximation of the error for one of the methods using a combination of the two. The two methods include a predictor (explicit) method and a corrector (implicit) method. The predictor method is only used to estimate the error (using the method described in the notes) whereas the corrector method is choosen for it's (usually) improved global behaviour.
Our implementation
For simplicity we have used low order methods (first order) which don't need to use multiple points. For our predictor we used the ubiquitous Euler Method and for our corrector we use the A-Stable Backwards Euler method. (So the global behaviour is improved for corrector).
Error estimation per unit step
In order to adjust our local error estimates into an estimate for global error we divide the error by the step size. This can have some surprising results - using 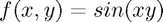 a step size of 10 is has smaller global error estimate than a step size of 1. This illustrates the important of being careful with choices of step size.
a step size of 10 is has smaller global error estimate than a step size of 1. This illustrates the important of being careful with choices of step size.
How do I use the program?
predictor_corrector_gui
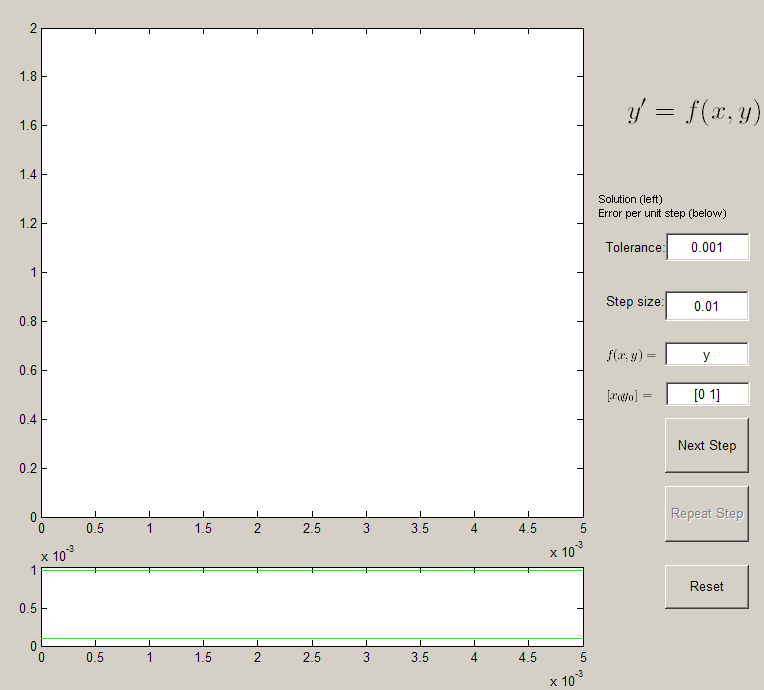
The large grid will plot the approximation to the solution computed, and the smaller box will display the error estimate per unit step. The two green lines are displaying the upper and lower bounds on the tolerance. (Any error above the upper line is too large, so reduce the step size and repeat the step, any error beneath the lower line means we are free to increase the step size).
Code
- predictor_corrector_gui.m (Run this)
- predictor_corrector_gui.fig (Required - GUI figure)
All files as .zip archive: predictor_corrector_all.zip

