QR Factorisation
The QR factorisation of a matrix 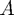 is its decomposition as the product where the matrix
is its decomposition as the product where the matrix 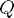 is orthogonal and the matrix
is orthogonal and the matrix 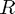 is upper triangular. Notice that the QR factorisation of a given matrix
is upper triangular. Notice that the QR factorisation of a given matrix 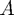 is not unique.
is not unique.
QR factorisation is often used to solve Linear Least Squares (LLS) problems, and it forms the basis for the QR Algorithm (see Part II), an iterative algorithm used to compute the eigenvalues and eigenvectors of a matrix.
Contents
Introduction
There are several ways in which the QR factorisation can be carried out. In what follows, we will mainly focus on two such ways, namely the method involving Householder reflections, and the method involving Givens rotations.
Householder reflections
A Householder reflection is a transformation of the form
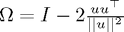
where 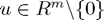 . Each such matrix is symmetric and orthogonal, and it can be shown that
. Each such matrix is symmetric and orthogonal, and it can be shown that 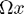 is the reflection of
is the reflection of 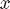 in the hyperplane orthogonal to
in the hyperplane orthogonal to 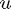 . Hence,
. Hence, 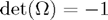 , and so
, and so 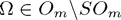 .
.
Givens rotations
A Givens rotation ![$\Omega^{[p,q]}$](qr_fac_eq93415.png) is an orthogonal transformation of determinant 1 (hence it's in
is an orthogonal transformation of determinant 1 (hence it's in 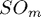 ) which coincides with the unit matrix, except at the four entries:
) which coincides with the unit matrix, except at the four entries:
![$\Omega^{[p,q]}_{p,p} = \Omega^{[p,q]}_{q,q} = \cos(\theta)$](qr_fac_eq69173.png)
![$\Omega^{[p,q]}_{p,q} = \sin(\theta)$](qr_fac_eq83603.png)
![$\Omega^{[p,q]}_{q,p} = -\sin(\theta)$](qr_fac_eq03407.png)
for some ![$\theta\in[-\pi,\pi]$](qr_fac_eq54407.png) .
.
Implementation
When implementing the Householder reflections method, we have been careful not to execute explicit matrix multiplication when computing
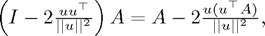
which is an 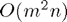 operation, but, as suggested in the notes, we have first evaluated
operation, but, as suggested in the notes, we have first evaluated
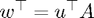 (in
(in 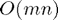 operations)
operations)
and then we have formed
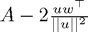 (also in
(also in 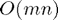 operations).
operations).
For large 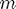 , this is way more efficient. See get_householder.m and do_householder.m
, this is way more efficient. See get_householder.m and do_householder.m
When implementing the Givens rotations method, we have made use of MATLAB's inbuilt command givens, which essentially returns the values of the required ![$\Omega^{[p,q]}$](qr_fac_eq93415.png) that differ from the identity. See get_givens.m
that differ from the identity. See get_givens.m
Moreover, the Givens rotation matrix has 'few' nonzero entries and so is sparse; this allows us to avoid doing a full matrix multiplication - we can get away with changing two rows. See do_givens.m
The GUI
Running the downloadable MATLAB® code on this page opens a GUI which demonstrates the QR algorithm.
IB_QR_GUI
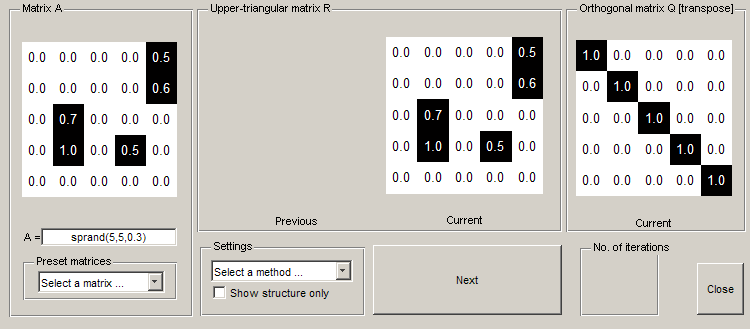
Interface
You can enter any square matrix you like, or use one of the preset matrices available. If you choose to use one of the preset matrices, you have a choice between sparse and dense matrices.
If you only want to see the structure of the matrices (represented by black for non-zero entries, white for zero entries, and grey for entries that differ from the previous matrix), you can click on the 'Structure only' radio button. By default the GUI shows both the structure and the values. Note that if your matrix or the values in it are large, it is advisable to switch to the 'structure only' mode because of overlap. As soon as you enter a matrix, it will appear on the far left. At the same time, the current matrix for 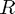 and the current matrix for
and the current matrix for 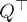 will appear.
will appear.
You can also select whether to use Householder reflections or Givens rotations to perform the QR algorithm. Notice that once you choose a method, you cannot change it during the iterations! The default method is Householder.
Once you have input the matrix (and chosen the method), you can start the QR algorithm by clicking on the 'Next' push button. You will see the new 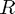 (in grey, you can see which rows have changed from the previous
(in grey, you can see which rows have changed from the previous 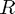 ), and the new
), and the new 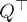 . To keep track of the number of iterations, there is a display on the right of the 'Next' push button. Keep going until the algorithm terminates (when the string 'Finished!' appears). To start a new iteration, input (or select) another matrix.
. To keep track of the number of iterations, there is a display on the right of the 'Next' push button. Keep going until the algorithm terminates (when the string 'Finished!' appears). To start a new iteration, input (or select) another matrix.
To close the GUI, click on the 'Close' push button.
The Code
- IB_QR_GUI.m (Run this)
- IB_QR_GUI.fig (Required)
- do_householder.m (Required - applies Householder)
- get_householder.m (Required - calculates Householder)
- do_givens.m (Required - applies Givens)
- get_givens.m (Required - calculates Givens)
All files as zip archive: qr_fac_all.zip

