Numerical Stability of Forms of the Interpolating Polynomial
Contents
Introduction
You have encountered two forms of the (unique!) interpolating polynomial of a function 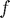 at nodes
at nodes 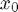 ,
, 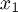 ,
, 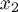 , ...
, ... 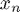 . These are the Newton form and the Lagrange form.
. These are the Newton form and the Lagrange form.
In lectures, you may have seen that the Newton form, evaluated using the Horner scheme, requires fewer operations than the Lagrange form.
However, the Newton form also has favourable numerical stability.
Numerical Stability
Roundoff error is a fundamental part of any numerical computation. Numerically stable methods attempt to control roundoff error and stop it from accumulating too quickly. This is not a rigorous definition, but it is clear that this property is certainly desirable.
The GUI
The MATLAB code downloadable below provides a visual comparison of the numerical stability of the Newton and Lagrange forms.
The function we interpolate is 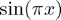 on the interval
on the interval ![$[0,0.2]$](stability_of_interpolation_eq01021.png) . We use equally spaced interpolation points.
. We use equally spaced interpolation points.
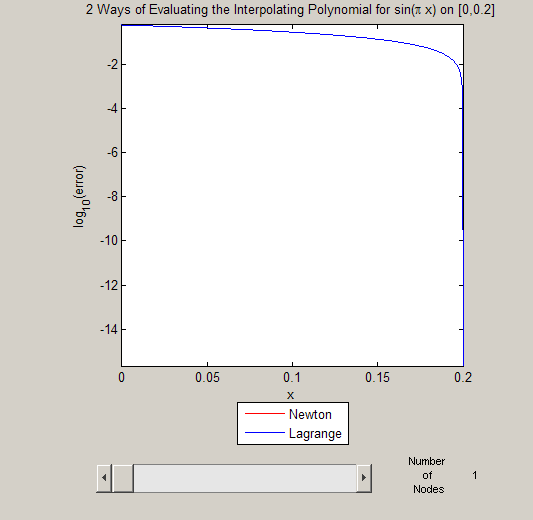
newton_stability(1);
The controls
The slider at the bottom sets the number of interpolation points.
The plot
The x-axis displays the position within the interval ![$[0,0.2]$](stability_of_interpolation_eq01021.png) .
.
The y-axis displays the base-10 logarithm of the absolute error at that position. Therefore it is roughly speaking:
- (# correct decimal digits - 1)
(If the absolute error is zero to within machine precision, it is replaced with eps)
Increasing the number of nodes
In the figure above, the Newton and Lagrange forms have very similar error.
Increasing the number of nodes we see:
newton_stability(7)
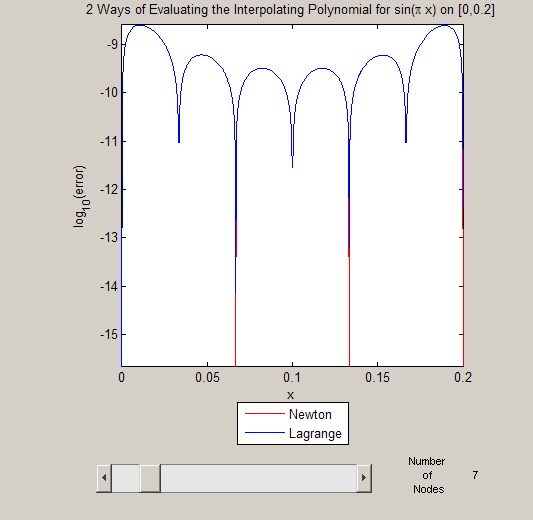
and the two forms again have very similar errors, with some slight discrepancies. Note that the error has decreased considerably for both forms. Going further:
newton_stability(9);
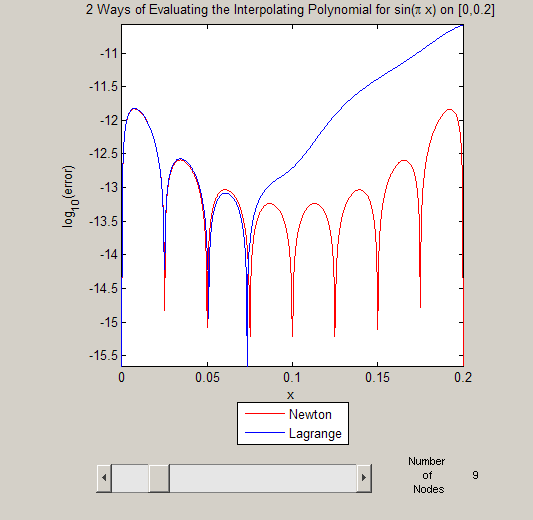
and the Newton form is now beginning to beat the Lagrange form. Now things get interesting:
newton_stability(12);
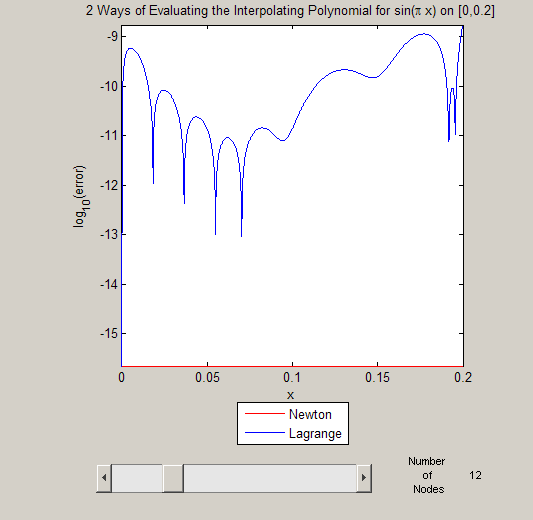
The Newton form seems to have reached machine precision, while the Lagrange form has gotten worse! This shows how the Lagrange form is not numerically stable. Since we can move the slider further, we take it all the way to the right:
newton_stability(50);
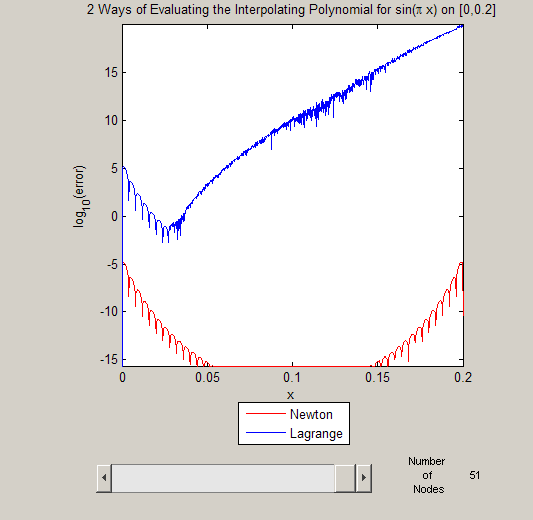
The Lagrange form has gone off into cloud-cuckoo-land, and even the Newton form is suffering from Runge's phenomenon (because of the equally spaced points).
Code
- newton_stability.m (Run this)
- newton_stability.fig (Required - GUI figure)
All files as .zip archive: stability_of_interpolation_all.zip

