Symplectic Numerical Integration
Contents
Introduction
In the IB and II Numerical Analysis Courses, we are concerned with the accuracy of solutions and related issues: how fast does the error decay? However, many equations in practice have special interesting properties: think of evolutions constrained to surfaces, or in physics, of conservation of energy. It makes sense to investigate how these properties are handled by various methods!
Preserving Phase-plane area
We consider the simple case of the ODE 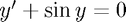 : the non-linear pendulum. Recall the concept of the phase-plane from IA Differential Equations: this is a plot of
: the non-linear pendulum. Recall the concept of the phase-plane from IA Differential Equations: this is a plot of 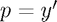 against
against 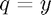 .
.
A map from the phase-plane to itself is said to be symplectic if it preserves areas. The flow-map of the ODE above, which evolves the system from 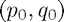 via the ODE, is one example of a symplectic map. It is not unreasonable then, to consider numerical methods inducing symplectic maps.
via the ODE, is one example of a symplectic map. It is not unreasonable then, to consider numerical methods inducing symplectic maps.
There is also a connection to conservation of energy. However, the 'energy' conserved by the symplectic numerical method will in general be different from the energy of the original system. But for a 'good' numerical method, the perturbed energy should be 'close'.
To show these concepts in action, we have produced an animation of a disc in the phase plane evolving under the ODE above. The numerical solution is produced by the Symplectic Euler (SE) [1] solver:
Although the evolution contorts the disc, it preserves the disc's original area.
Comparison (Short-term)
How does SE fare against other solvers, say the now-familiar (Explicit/Forward) Euler (EE) method or the built-in solver ode45? The following animation demonstrates.
The evolution should be along an ellipse, and it's clear that EE goes completely astray. SE and ode45 fare better. Note that the ellipse-shaped orbit for SE is slightly rotated relative to that for ode45. It is also rotated relative to the exact trajectory - remember that symplectic methods conserve the energy of a modified system.
Comparison (Long-term)
In some sense, the previous comparison is not terribly fair: SE is a first-order method while ode45 is a high-order Runge-Kutta method with error control! However, there is a sense in which SE still does better: conservation of energy. This requires a very long-term investigation: we just plot the result below as a single image: (Program symplectic_test_long_time_behaviour.m generates the following image WARNING: it takes quite a long time)
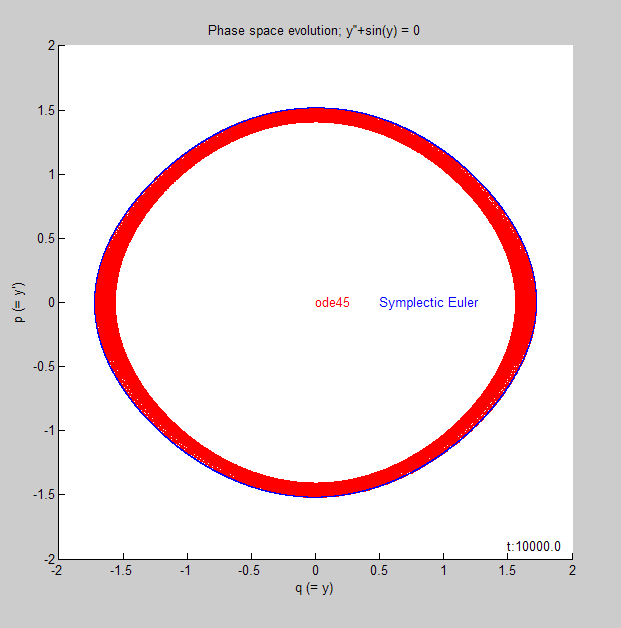
The thick red ellipse is the result of the trajectory of the ode45 solution slowly spiralling in towards the origin. It should not do this! The SE trajectory, however, remains thin.
Further Reading
[2] is a good, if obvious place to start. Chapter 5 of [3] is an excellent (if purer) introduction to the main themes of numerical methods that preserve special properties of equations. Another symplectic integrator is [4].
References
[1] http://en.wikipedia.org/wiki/Symplectic_Euler_method
[2] http://en.wikipedia.org/wiki/Symplectic_integrator
[3] A First Course in the Numerical Analysis of Differential Equations; Arieh Iserles
[4] http://en.wikipedia.org/wiki/Verlet_integration
Code
All files as zip archive: symplectic_integrators_all.zip
WARNING! The avi files produced are quite large.

