Chebyshev Methods for Differential Equations and Example Sheet 2, Question 20
We are already familiar with using Spectral methods to find solutions to differential and partial differential equations. However, there is a significant restriction as to the applicability of spectral methods: spectral convergence depends on both analyticity and periodicity of the problem (including boundary conditions!) So in order to make use of spectral methods in the general case, we need to be more careful...
Contents
Chebyshev methods
Letting 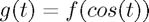 , therefore if we can extend
, therefore if we can extend 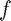 onto an open neighbourhood of
onto an open neighbourhood of ![$[-1,1]$](chebyshev_eq85290.png) we find that
we find that 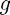 is both analytic and periodic, with period
is both analytic and periodic, with period 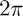 . This enables us to employ methods which converge with spectral speeds.
. This enables us to employ methods which converge with spectral speeds.
Chebyshev expansion and Chebyshev deriviatives
Since the Chebyshev polynomials are a complete orthonormal spanning set on ![$[-1,1]$](chebyshev_eq85290.png) we can write
we can write
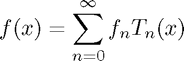
The coefficients 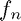 can be related to Fourier coefficients of
can be related to Fourier coefficients of 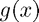 and therefore we see that they converge spectrally.
and therefore we see that they converge spectrally.
Since the 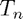 are also polynomials of degree
are also polynomials of degree 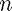 , we know that their derivatives are polynomials of degree
, we know that their derivatives are polynomials of degree 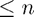 so they must have an expansion in terms of
so they must have an expansion in terms of  . In the Lecture Notes there is a demonstration of how to do this.
. In the Lecture Notes there is a demonstration of how to do this.
How to use this method in practice
MATLAB® represents polynomials as vectors of the coefficients. Taking note of this and using it to represent Chebyshev expansions as vectors in the coefficients, we store: 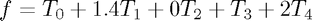 as
as
f = [1 1.4 0 1 2]';
In order to take deriviatives of 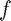 we can use a linear map taking our vector to it's derivative. This vector will have the form:
we can use a linear map taking our vector to it's derivative. This vector will have the form:
n = 7; D = zeros(n); for i = 1:n if mod(i,2) == 1 D(2*(1:((i-1)/2)),i) = 2*(i-1); else D(1,i) = i-1; D(2*(2:((i)/2))-1,i) = 2*(i-1); end end D
D =
0 1 0 3 0 5 0
0 0 4 0 8 0 12
0 0 0 6 0 10 0
0 0 0 0 8 0 12
0 0 0 0 0 10 0
0 0 0 0 0 0 12
0 0 0 0 0 0 0
It is easy to see the structure we expect in this matrix: the first column is all zeros (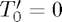 ), the other columns have alternate zero and non-zero entries as expected from the forms of the derivatives in the notes. (1)
), the other columns have alternate zero and non-zero entries as expected from the forms of the derivatives in the notes. (1)
Solving an equation
We are going to investigate 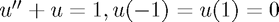 on the interval
on the interval ![$[-1,1]$](chebyshev_eq85290.png) . We can solve this using A-level methods reasonably easily:
. We can solve this using A-level methods reasonably easily: 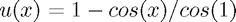 . However, we are going to solve this using the Chebyshev method.
. However, we are going to solve this using the Chebyshev method.
Firstly we can show that the odd coefficients are 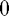 and the even coefficients satisfy
and the even coefficients satisfy 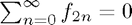 . (Filling in the details of this is (a) on the example sheet.
. (Filling in the details of this is (a) on the example sheet.
Now we want to solve the method by truncating the Chebyshev series expansion of  and solving on a finite domain. We also need to be careful about how we will be treating "ignoring" the odd coefficients.
and solving on a finite domain. We also need to be careful about how we will be treating "ignoring" the odd coefficients.
Ideally, we want to represent our problem as a linear system: 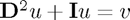 where
where 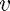 is the vector formed by taking the Chebyshev expansion of the forcing term
is the vector formed by taking the Chebyshev expansion of the forcing term 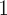 . In order to ignore the odd terms, we compute
. In order to ignore the odd terms, we compute 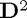 and then only take out the even rows and columns. This will then act on the subspace we would like to consider. We also need to work out a way to force the linear system to consider the bounday conditions:
and then only take out the even rows and columns. This will then act on the subspace we would like to consider. We also need to work out a way to force the linear system to consider the bounday conditions: 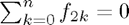 . We can do this by including another row in our matrix and forcing this to equal
. We can do this by including another row in our matrix and forcing this to equal 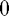 as well. Therefore our final system will look something like this:
as well. Therefore our final system will look something like this:
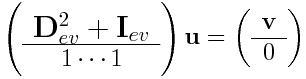
We can set up and solve equations like this very quickly in MATLAB®. One thing to notice about this equation is that we are overconstrained. Therefore when we solve this equation we could take some kind of least squares approximation. MATLAB® includes the function lsqlin which enables us to give a constraint even more importance. Therefore by setting up our equation so that the boundary condition must be satisfied we can obtain solutions which statisfy them. (The alternative method of doing least squares to find a solution which is close to satisfying the boundary conditions is also implemented).
Plots of solution
hold on; for n = 1:15 v = zeros(n,1); v(1) = 1; u = chebyshev_solv(n,v); u = pad_ev(u); x = -1:0.01:1; plot(x,evaluate_cheb(u,x)); end plot(x,1-cos(x)/cos(1),'r'); hold off;
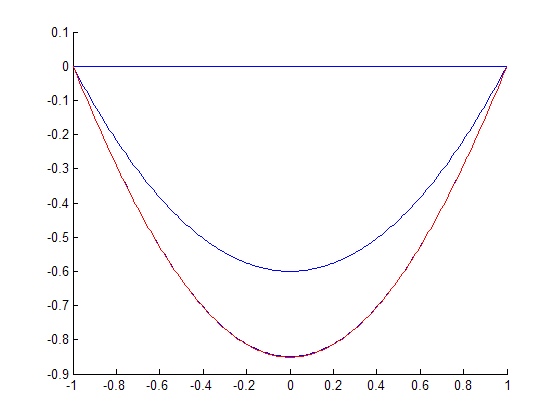
The solution, even for very small 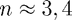 is very close to the actual solution, illustrating the power of spectral convergence.
is very close to the actual solution, illustrating the power of spectral convergence.
Notes
(1) This is not necessarily the best way to implement this method. The matrix 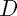 contains many zero elements so in practice it is faster to use a for loop or similar to form the derivative. However, this is more than fast enough for our methods.
contains many zero elements so in practice it is faster to use a for loop or similar to form the derivative. However, this is more than fast enough for our methods.
Code
See above examples for usage.
- chebyshev_solv.m
- chebyshev_mat.m (Required by chebyshev_solv.m)
- pad_ev.m
- evaluate_cheb.m
All files as .zip archive: chebyshev_all.zip

