Fast Fourier Transforms
Contents
Introduction
Fast Fourier Transforms (FFT) are a faster version of the Discrete Fourier Transforms (DFT), whose importance cannot be underestimated, given the copious amount of applications they have (spectral analysis, PDEs, image processing, filtering, ...).
Theory and relevant bits of the notes
Essentially, what general Fourier transforms do is to switch from a time domain representation of a given function 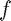 to a dual frequency domain representation. Some operations and computations which are not too easy in the time domain become almost trivial in the frequency domain (for example, differentiation in the time domain becomes multiplication in the frequency domain). By applying a relevant inverse transform, one can usually go back to the time domain representation without any loss of information.
to a dual frequency domain representation. Some operations and computations which are not too easy in the time domain become almost trivial in the frequency domain (for example, differentiation in the time domain becomes multiplication in the frequency domain). By applying a relevant inverse transform, one can usually go back to the time domain representation without any loss of information.
The aim of this GUI
Running the downloadable MATLAB® code on this page opens a GUI which allows you to play with the FFT and see how the algorithm works. To complement this GUI, there is also an animation: see Animation below.
Without further ado, here is the GUI.
FFT2_GUI
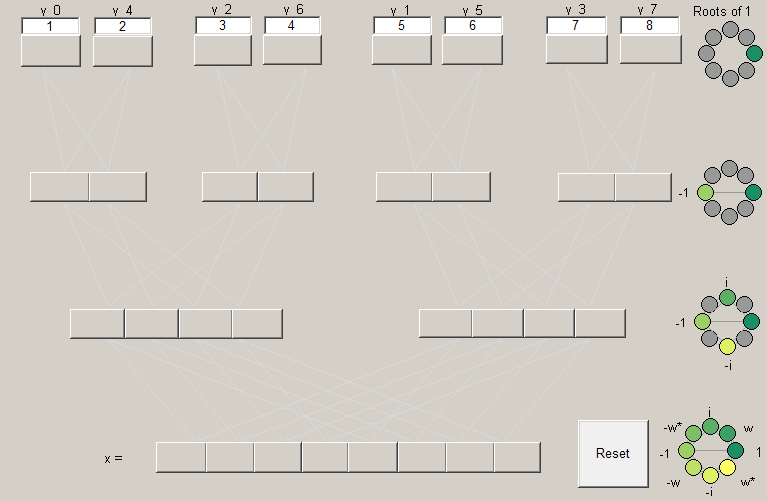
The interface
In the editable boxes, you can plug in the components of the vector  of length 8 for which you want to find the inverse FFT
of length 8 for which you want to find the inverse FFT 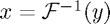 . You will notice that the ordering of the entries of
. You will notice that the ordering of the entries of 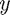 is not the usual one, to emphasise the binary nature of the construction. If you want to see how this ordering was achieved, look again at the animation by clicking on FFTanimation.m. The preset
is not the usual one, to emphasise the binary nature of the construction. If you want to see how this ordering was achieved, look again at the animation by clicking on FFTanimation.m. The preset  is
is 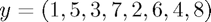 .
.
If you click on any of the push buttons in the FFT scheme, the button will light up in a specific color, and a value will appear on it. Also, you will see the tree showing how the value has been computed. The color specifies the rule by which that entry has been computed: if the entry has color  , it means that its value is the result of the calculation
, it means that its value is the result of the calculation
(left-hand child) + (the root of unity corresponding to 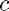 )*(right-hand child)
)*(right-hand child)
which corresponds, of course, to the rule given in Lecture 4 to compute the entries of 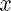 . To know what is the root of unity corresponding to a given colour
. To know what is the root of unity corresponding to a given colour 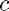 , there are diagrams next to each iteration level. Notice that what in the diagrams is labeled as 'w' corresponds to the root of unity
, there are diagrams next to each iteration level. Notice that what in the diagrams is labeled as 'w' corresponds to the root of unity 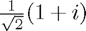 , and an asterisk '*' means complex conjugation.
, and an asterisk '*' means complex conjugation.
To give an example, say you click on the fourth button from the left on the second row from the top. The color you will see is a light green, which corresponds to the 2nd root of unity 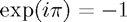 . This means that the value of that entry is given by
. This means that the value of that entry is given by
(value of third button from the left on first row from the top) + (-1)*(value of fourth button from the left on first row from the top).
To reset the FFT scheme, just click on the Reset push button, and, likewise, to close the GUI, just click on the Close push button.
Animation
This shows (for  ), how to do the decomposition into even and odd parts. Red means 'even part' and black means 'odd part' (of the vector considered at that point in the video).
), how to do the decomposition into even and odd parts. Red means 'even part' and black means 'odd part' (of the vector considered at that point in the video).
Code
- FFT2_GUI.m (Run this)
- FFT2_GUI.fig (Required - GUI figure)
All files as .zip archive: fft_gui_all.zip

