Multigrid methods
One of the difficulties when talking about relative speeds of numerical methods is trying to get a hand on the speed up for various methods. This demonstration of the multigrid method shows how much better than Jacobi and Gauss-Seidel are for solving linear systems.
Contents
The theory
The general idea of multigrid is that convergence for Gauss-Seidel depends on the frequency of the solution relative to the grid size. By applying Gauss-Seidel on a variety of different grid sizes this effect can be used to great effect. The most basic form of multigrid inolves solving the Poisson equation by finite differences on a grid. This reduces to a matrix equation 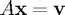 . In order to solve this equation we apply Gauss-Seidel a few times on a full size grid, before restricting the problem to a smaller grid and repeating the process. Once we've solve reduce the grid sufficiently many times we can solve the linear system and prolongate the solution to larger grid sizes.
. In order to solve this equation we apply Gauss-Seidel a few times on a full size grid, before restricting the problem to a smaller grid and repeating the process. Once we've solve reduce the grid sufficiently many times we can solve the linear system and prolongate the solution to larger grid sizes.
The GUI
The GUI solves the 1D Poisson equation 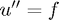 on a grid size of
on a grid size of 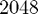 with zero boundary conditions. We've picked the function
with zero boundary conditions. We've picked the function 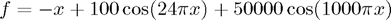 to ensure a range of frequencies.
to ensure a range of frequencies.
multigrid_gui
You can alter the method used to solve this system: relaxed Jacobi, Gauss-Seidel or multigrid and can see just how much quicker multigrid is than these two other methods.
References
The code for this project is based on Professor Demanet's code found on his course page
Code
- multigrid_gui.m (Run this)
- multigrid_gui.fig (Required)
All files as .zip archive: multigrid_all.zip

