Stability of Finite Difference Methods
The stability of finite difference methods is essential to using an appropriate methods for computing numerical solutions
Contents
Introduction
We can solve various Partial Differential Equations with initial conditions using a finite difference scheme. The diffusion equation, for example, might use a scheme such as:
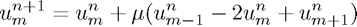
Where 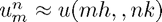 a solution of
a solution of  and
and 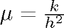 .
.
Implementation
We can implement these finite difference methods in MATLAB using (sparce) Matrix multiplication. Using the example given above we have:

Generating this sparce, tridiagonal matrix can be done using the spdiags function. For example (with 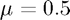 ):
):
e = ones(5, 1); A = spdiags( [0.5*e (1-2*0.5)*e 0.5*e], -1:1, 5, 5); disp(full(A))
0 0.5000 0 0 0
0.5000 0 0.5000 0 0
0 0.5000 0 0.5000 0
0 0 0.5000 0 0.5000
0 0 0 0.5000 0
full is necessary to display the whole matrix rather than the sparce data which is is holding.
For other methods we modify the matrix, or matrices, for each time step by the method is the same. For a full implementation see ...
Stability and Convergence
An important feature that we wish our methods to have is convergence: (roughly) as mesh size tends to zero, we want our numerical solution to tend (uniformly) to the true solution.
In the lecture notes, we can see the for the method discussed above convergence depends on 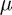 .
.
The lecture notes also define what it means for a numerical method to be stable: (roughly) the numerical method remains bounded (in a given interval) for zero boundary conditions. From the Lax equivalence theorem, we are given that for suitable PDEs and methods with error 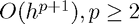 stability and convergence are equivalent.
stability and convergence are equivalent.
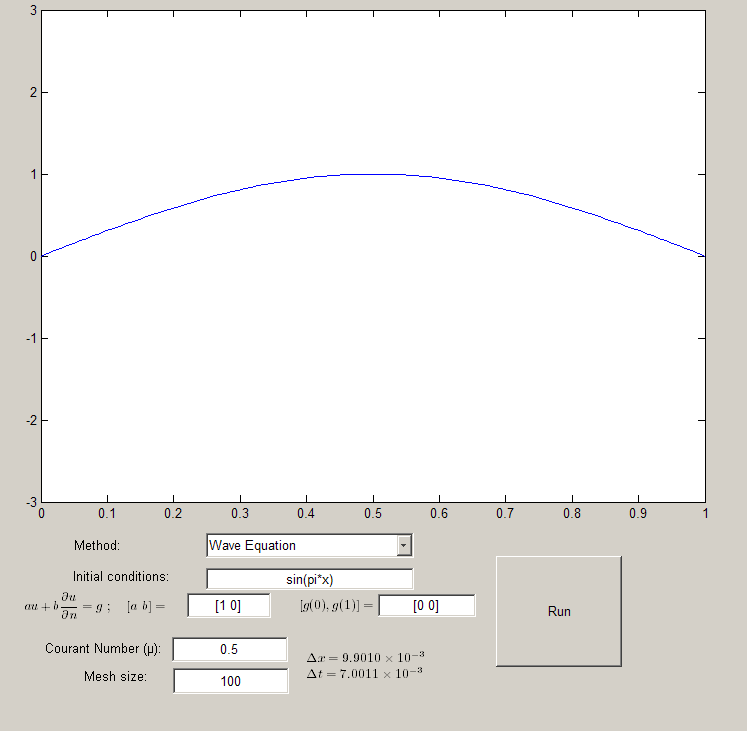
The GUI
Running the downloadable MATLAB code on this page opens a GUI which allows you to experiment with varying Courant numbers, methods, initial conditions and mesh size.
stability
The Diffusion Equation (Euler Method)
This is the method which has already been discussed earlier on this page. We know from our notes that this will be stable for 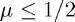 and unstable for
and unstable for 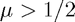 . Try using
. Try using 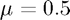 and
and 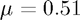 . The wave will move very slowly (each timestep for a mesh size of 100 will be:
. The wave will move very slowly (each timestep for a mesh size of 100 will be: 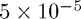 ) however, if we want to take larger steps through time (
) however, if we want to take larger steps through time (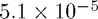 for instance) the method becomes unstable.
for instance) the method becomes unstable.
The Diffusion Equation (Crank-Nicolson)
We obtained the Euler Method by applying the Euler method to the semidiscretization 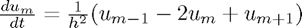 . Using the trapezoidal rule we obtain the Crank-Nicolson method which is stable for all
. Using the trapezoidal rule we obtain the Crank-Nicolson method which is stable for all 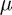 . This means we can choose larger time steps and not suffer from the same instabilities experienced using the Euler Method
. This means we can choose larger time steps and not suffer from the same instabilities experienced using the Euler Method
The Wave Equation
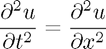
By approximating both second derivatives using finite differences, we can obtain a scheme to approximate the wave equation. The main difference here is that we must consider a second set of inital conditions: 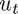 . For the purposes of the illustration we have assumed that this is
. For the purposes of the illustration we have assumed that this is  .
.
The method obtained in this way is stable for 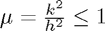 . The additional power of
. The additional power of 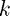 means that we can take
means that we can take 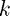 and
and 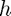 to be similar in order and remain stable. (Although we must ensure that
to be similar in order and remain stable. (Although we must ensure that 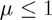 . Try running the wave equation for
. Try running the wave equation for 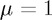 and
and 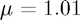
Initial conditions
You can choose your own initial conditions - some which you might like to try include 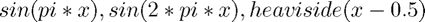 .
.
Boundary conditions
It is also possible to change the boundary conditions which the methods use. The general boundary conditions can be "Robin" boundary conditions: 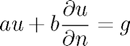 $ on the boundary of the domain. On the case of the domain
$ on the boundary of the domain. On the case of the domain ![$[0,1]$](pde_stability_eq78179.png) this reduces to:
this reduces to: 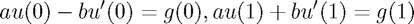 $ From this general form, we can obtain Dirichlet boundary conditions - letting
$ From this general form, we can obtain Dirichlet boundary conditions - letting 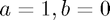 and Neumann boundary conditions - letting
and Neumann boundary conditions - letting 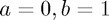 .
.
The way in which the code implements boundary conditions is somewhat special. For Dirichlet boundary conditions it is reasonably simple, since we just need to fix the values 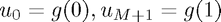 . For Neumann boundary conditions we could use the one-sided approximation of the normal deriviative
. For Neumann boundary conditions we could use the one-sided approximation of the normal deriviative 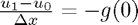 but this would only yeild a first order method. In order to sustain a second order method, we need to be more careful about our choice of approximation for
but this would only yeild a first order method. In order to sustain a second order method, we need to be more careful about our choice of approximation for 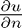 .
.
The way we do this involves introducing "Ghost points" which are never actually used or referenced in the code, 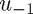 and
and 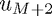 . Then we can use a symmetric approximation to the normal deriviative:
. Then we can use a symmetric approximation to the normal deriviative: 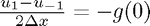 . This allows us to compute a value for our ghost point (
. This allows us to compute a value for our ghost point (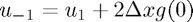 ). We can then plug this into the general form of our equation.
). We can then plug this into the general form of our equation.
Working out Robin conditions involves using the same process as for Dirichlet conditions again.
Code
- stability.m (Run this)
- stability.fig (Required - GUI figure)
All files as .zip archive: pde_stability_all.zip

