Preconditioning
Preconditioning is a technique (not peculiar to just the CG method) consisting in preconditioning the system that we want to solve, so that the new system has better properties (e.g. faster convergence to the solution of numerical methods, less cost of computation,...). The solution to the original problem can be easily contructed from the solution of the preconditioned problem. Usually the main aim of preconditioning is to reduce the condition number of the problem.
Contents
Theory
Instead of solving the system 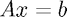 , we precondition the system and try to solve the system
, we precondition the system and try to solve the system
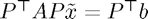 if we want to use split preconditioning, where
if we want to use split preconditioning, where  ,
,
or
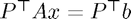 if we want to use left preconditioning.
if we want to use left preconditioning.
Since we want to apply the CG method, we need to make sure that 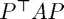 (if we use split preconditioning) or
(if we use split preconditioning) or 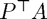 (if we use left preconditioning) is SPD.
(if we use left preconditioning) is SPD.
We can then apply the CG method to the preconditioned system. In the case of split preconditioning, the preconditioned solution is related to the original solution by 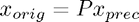 , while for the left preconditioning the solutions of the original and of the preconditioned systems coincide.
, while for the left preconditioning the solutions of the original and of the preconditioned systems coincide.
The GUI
Running the downloadable MATLAB® code on this page opens a GUI which allows you to play with preconditioning.
precond_GUI
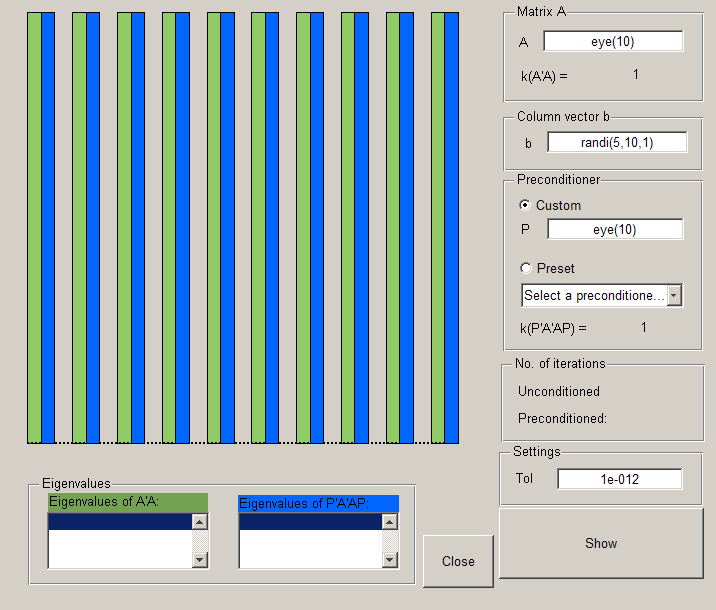
Interface
You can input the matrix 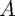 and the column vector
and the column vector 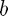 of the system
of the system 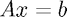 , and can also decide whether you want to input the preconditioner
, and can also decide whether you want to input the preconditioner 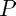 manually, or choose between some preset preconditioners (option available only if you are using split conditioning). You can also set the tolerance, which determines the degree of precision of the numerical method in finding the solution.
manually, or choose between some preset preconditioners (option available only if you are using split conditioning). You can also set the tolerance, which determines the degree of precision of the numerical method in finding the solution.
If you decide to use the split conditioning, you just need to make sure that the input square matrix 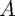 is SPD. A quick way to generate such an
is SPD. A quick way to generate such an 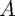 is to do:
is to do:
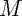 = any non-singular matrix
= any non-singular matrix
A = 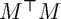 .
.
For 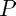 , you can then input any non-singular square matrix of the same dimensions of
, you can then input any non-singular square matrix of the same dimensions of 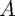 . The conditioned matrix
. The conditioned matrix 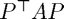 will still be SPD.
will still be SPD.
If you decide to use left conditioning, things are trickier since you need to make sure that the preconditioner 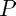 is such that
is such that 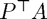 is SPD, otherwise the method will not converge.
is SPD, otherwise the method will not converge.
When you input 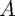 or
or 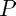 , the condition numbers
, the condition numbers 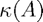 and
and 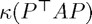 (split) or
(split) or 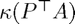 (left) will appear automatically. Play with
(left) will appear automatically. Play with 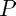 to see how the condition numbers change.
to see how the condition numbers change.
When you have input all the relevant stuff, click on 'Show' to display the number of iterations for both the original and the preconditioned system, the eigenvalues of 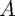 and
and 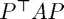 (split) or
(split) or 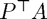 ( left), and a bar chart displaying the spectrum of
( left), and a bar chart displaying the spectrum of 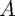 in green, and the spectrum of the preconditioned matrix in blue (so that you can see how preconditioning redistributes the spectrum, and hence changes the condition number).
in green, and the spectrum of the preconditioned matrix in blue (so that you can see how preconditioning redistributes the spectrum, and hence changes the condition number).
The Code
Code
- precond_GUI.m (Run this)
- precond_GUI.fig (Required - GUI figure)
All files as .zip archive: precond_all.zip

