QR Algorithm - Demonstration of structure
Contents
Introduction
The QR algorithm is an iterative method to find eigenvalues and eigenvectors of a given matrix. The algorithm in itself is very straightforward:
1. Let 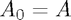 .
.
2. For 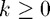 , compute the QR factorisation
, compute the QR factorisation 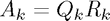 .
.
3. Set 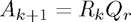 .
.
It is interesting to see the effect of the QR algorithm on a given matrix 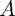 , to see why it works. This is the purpose of this GUI.
, to see why it works. This is the purpose of this GUI.
For more properties of the QR algorithm, see the Part II lecture notes.
The GUI
Running the downloadable MATLAB® code on this page opens a GUI which demonstrate the effects of the QR Algorithm on a matrix of your choice. The matrix must be a square matrix.
QR_hex_GUI

To visually read what is going on at each iteration, the convention used is the following:
- The bigger the magnitude of the entry, the bigger the size of the hexagons. For stylistic reasons, all the hexagons corresponding to entries whose magnitudes are bigger than a certain prefixed value have the same maximal size.
- The bigger the magnitude of the entry, the brighter the shade of green.
The interface
Edit box A = : You can enter any square matrix you like here. Alternatively, you can select one randomly generated symmetric or upper Hessenberg matrix from the QR-invariant structure pop-up menu (see later). Notice that the larger the size of the matrix, the slower the animation will be. For the educational purposes of the GUI, a 20x20 matrix will suffice. The preset matrix is a random 20x20 integer matrix.
Edit box No. of iterations: : Here you can enter the number of iterations you want to see. The preset number of iterations is 0.
WARNING: On Windows 7®, the program might give NaN values at some point. In this case, the GUI will automatically stop the animation.
Push button Start! : Press this button to start the animation. Once the animation has been stopped, pressing the start button again will NOT resume the animation, but start it again from the beginning.
Push button Stop : Press this button to stop the animation.
Text box Iteration no. : This keeps track of the current iteration number.
Panel Eigenvalues : On the LHS of this panel, the values of the (1,1)th and (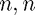 )th entries of the iteration matrix
)th entries of the iteration matrix 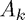 (where
(where 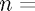 dim(
dim(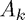 )) are shown. On the RHS of the panel, a list of the eigenvalues of the original matrix
)) are shown. On the RHS of the panel, a list of the eigenvalues of the original matrix 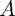 is shown.
is shown.
Pop-up menu QR-invariant structures : Here you can select a randomly generated 20x20 symmetric matrix, or a randomly generated 20x20 upper Hessenberg matrix. Both these kinds of matrices have their structures preserved by the QR algorithm.
Note: The function randS which generates the random symmetric matrix is a function we have defined (it is not built-in). The code is as follows:
function M = randS( n ) % random symmetric matrix M=rand(n); M=triu(M)+triu(M,1)';
Push button Close : Press this button to close the GUI.
The Code
- QR_hex_GUI.m (Run this)
- QR_hex_GUI.fig (Required)
All files as zip archive: qr_hex_all.zip

