Stencils and Image Manipulation

Contents
Introduction
Stencils are a useful shorthand and calculational tool on grids. For example, the 5-point approximation to 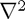 from lectures can be represented by the (hopefully increasingly familiar) stencil
from lectures can be represented by the (hopefully increasingly familiar) stencil
laplace5pt = [ 0 1 0; 1 -4 1; 0 1 0]; display(laplace5pt);
laplace5pt =
0 1 0
1 -4 1
0 1 0
Review
Stencils as Image Transformations
In this unit we explore a few more stencils by using them to represent an image transformation. After all, a digital image in MATLAB is just an array of numbers representing colour values. By applying the stencil to each point of the original image, and storing each result, we produce a new image. Many interesting image transformations can be carried out in this way.
The GUI
Running the downloadable MATLAB code at the bottom of this page starts a Graphical User Interface (GUI):
stencil_demo
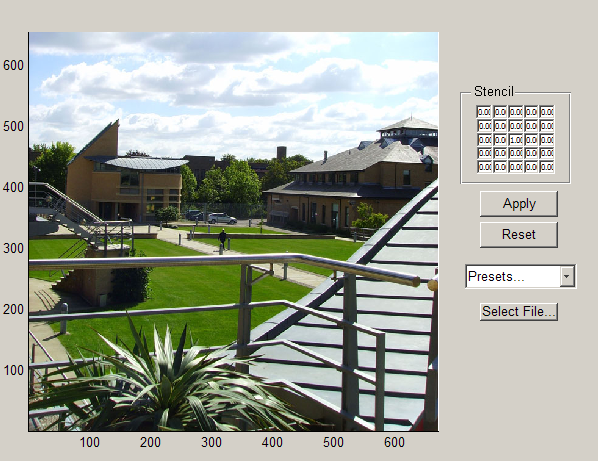
On the right-hand side there is a representation of the stencil
identity = zeros(5,5); identity(3,3)=1; display(identity);
identity =
0 0 0 0 0
0 0 0 0 0
0 0 1 0 0
0 0 0 0 0
0 0 0 0 0
This stencil is not very exciting; it just represents the identity transformation which leaves the image completely unchanged.
You can apply a stencil of your choice by entering it into the text boxes and clicking the 'Apply' button. To return to the orignal image after a series of stencils have been applied, press the 'Reset' button.
Preset Stencils
Notice the popup menu entitled 'Preset Stencils...'; here we have included some standard stencils so that you don't need to type them in yourself. These are explained in more detail below.
Note that we take 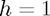 (the grid spacing is 1 pixel) in all stencils.
(the grid spacing is 1 pixel) in all stencils.
Laplacian (5pt)
This is the 5-point approximation to 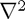 mentioned in the Introduction:
mentioned in the Introduction:
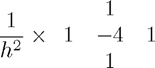
Laplacian (9pt)
This is a 9-point approximation to 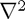 with stencil:
with stencil:
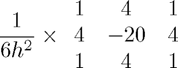
Biharmonic (13pt)
This is a 13-point approximation to 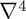 with stencil:
with stencil:
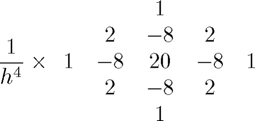
Simpson's Rule (9pt)
This is a 9-point approximation to the two-dimensional integral with stencil:
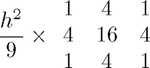
Gaussian Blur (9pt)
This is a stencil
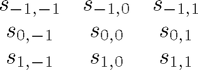
with
![$$s_{i,j}=\frac{1}{\sqrt{2\pi \sigma^2}} \exp \left[ -\frac{1}{2\sigma^2} \left( i^2 + j^2 \right) \right]$$](stencil_eq23223.png)
In this case, we take 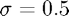 . More information can be found at http://en.wikipedia.org/wiki/Gaussian_blur
. More information can be found at http://en.wikipedia.org/wiki/Gaussian_blur
Code
- stencil_demo.m (Run this)
- stencil_demo.fig (Required)
- photo1.jpg (Required - test photo)
All files as .zip archive: stencil_all.zip

