Researcher: Yury Korolev, Martin Burger, Carola-Bibiane Schönlieb, Leila Muresan

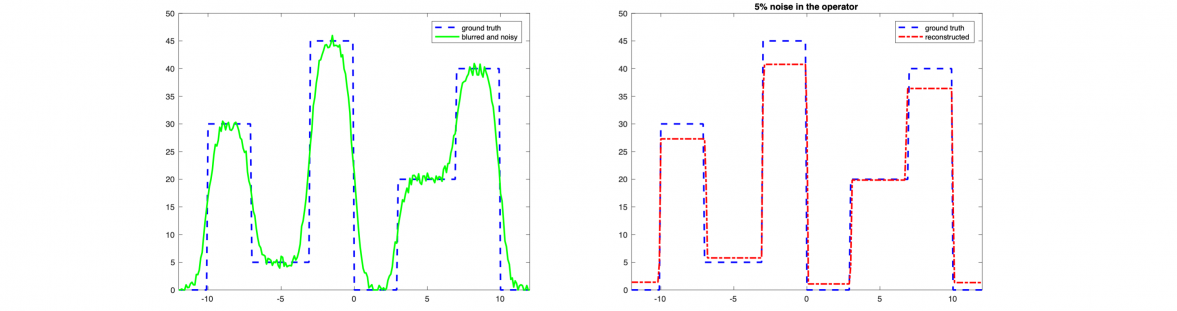
Inverse problems are widely used in situations where direct measurements are either too costly or impossible and quantities of interest need to be reconstructed from indirectly measured data. This is usually done by 'inverting' a mathematical model that describes the data acquisition. Careful analysis of the uncertainties associated with the inversion is key to the design of stable numerical algorithms. There are two sources of uncertainty that need to be considered: uncertainty associated with the data and uncertainty associated with the models. Data uncertainty typically is due to noise and finite precision of measurement devices, whilst model uncertainty reflects the simplified nature of the available models that cannot capture the phenomena involved in data acquisition in their full complexity. 
We are developing an approach to quantification of both types of uncertainty using the apparatus of partially ordered spaces. Partial order is attractive both from the methodological point of view, enabling a detailed description of data and model uncertainty, and from the point of view of computational efficiency, allowing one to stay in the convex setting in situations when standard methods lead to non-convex optimisation problems. 
This approach is particularly promising in image deblurring which is often used to ikprove the quality of microspy images. We are currently collaborating with Dr Leila Muresan from the Cambridge Advanced Imaging Centre on spatically variable image deconvolution in lightsheet microscopy.