
European Centre for Medium Range Weather Forecasts,
talk given at the ECMWF Seminar of 5 September 2005
Reproduced below are the slides for my talk, plus a few I had no time to show. The talk discussed three main ideas -- three of the most crucially important, though elementary, ideas from fluid dynamics -- each with a direct bearing on atmospheric chemistry. The first begins with something you can find in any good fluid-dynamics textbook, but so important that it can't not be mentioned. The second and third aren't in the textbooks at all. (Actually, with the third it's worse: there are well-entrenched myths that directly impede understanding.) The three ideas are
The last idea illustrates one of the grand themes of physics, the dynamical organization of fluctuations. It is essential for understanding, for instance, the way the stratospheric Brewer-Dobson circulation is driven. (Contrary to a well-entrenched myth, the circulation is not directly driven by solar heating. It is not so driven any more than, to quote Sir James Jeans, ``the thermometer keeps the room hot''.)
The slides draw on material from my core lectures in our annual Summer School in Geophysical and Environmental Fluid Dynamics as well as from the various reviews I've been asked to write over the years, the most comprehensive of which is reference [1].
The first slide recalls how the velocity field called `pure strain' arises when analysing a general velocity field in the neighbourhood of a material point. The pure strain contribution is that shown in the box at bottom right. If the whole velocity field consists of nothing but pure strain, then it is `irrotational'. with zero vorticity (and conspicuously unreal!)
Slide 1:

The next gives a specific example (pure shear) of a rotational flow having pure strain as well as vorticity (the nonzero rotational contribution characteristic of almost all real flows).
Slide 2:

Now think about a general flow in which the strain rate, α, varies randomly in magnitude, and the directions of the principal strain axes also vary randomly. Very robustly, material line elements tend to thin and lengthen exponentially fast, because there is a statistical bias due to the tilting of the line element by the strain itself:
Slide 3:
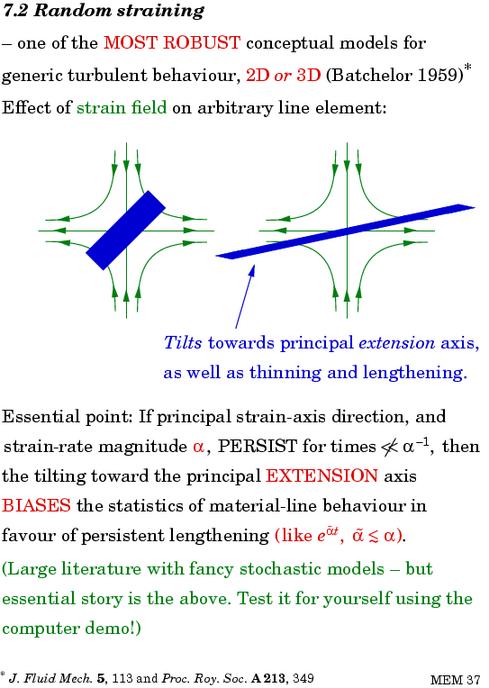
The computer demo just mentioned is from the hands-on computer lab in the Summer School. It's available for download from the Summer School website. Playing with it will show you how robust is the tendency for material line elements to thin and lengthen.
There are some important exceptions to this rule of exponentially fast thinning and lengthening:
Slide 4:

Slides 5-8 show some results from reference [2], in a hemispheric polar stereographic projection, illustrating the persistent lengthening of material line elements in the midlatitude `surf zone' of a model stratosphere. The shapes of ten material contours were computed offline from the stratospheric model's velocity field by the `contour advection' technique. This work and the independent work of reference [3] were the first to use this exquisitely accurate adaptive, trajectory-based technique, previously developed to high sophistication by David Dritschel, as a benchmark tracer-advection algorithm:
Slide 5:
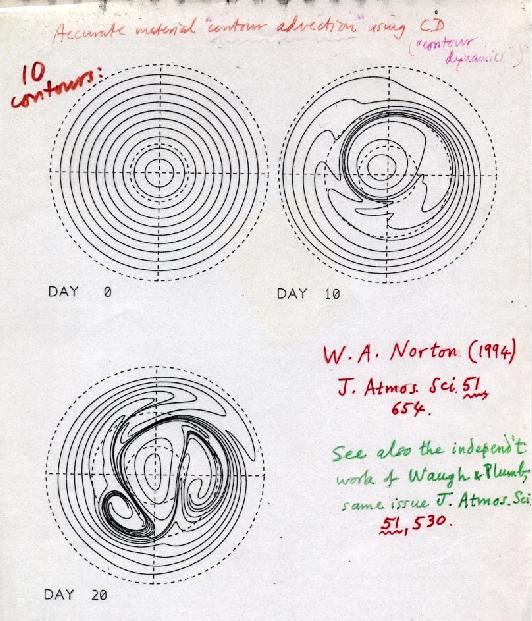
Slide 6:
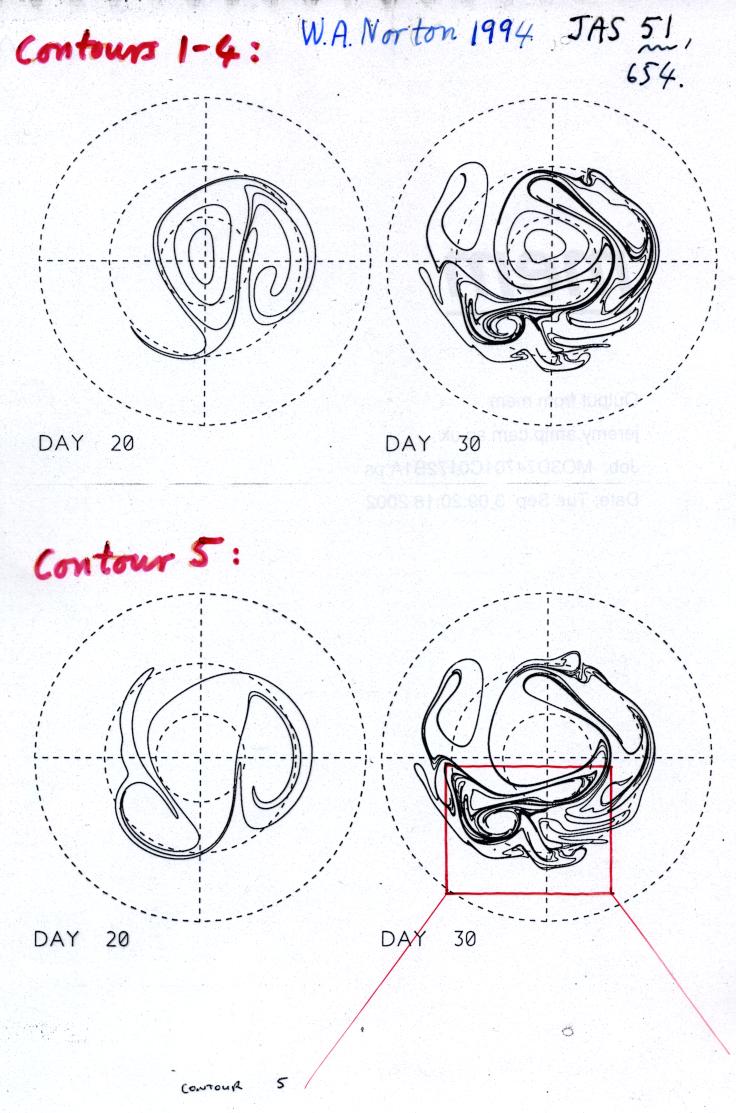
Zooming in to the marked box: the contour-advection algorithm shows up just how intricate is the irreversible deformation of contour 5 -- this is turbulent, not wavelike! (By contrast, the contours within the polar vortex, contours 1 and 2, have wavelike behaviour.)
Slide 7:
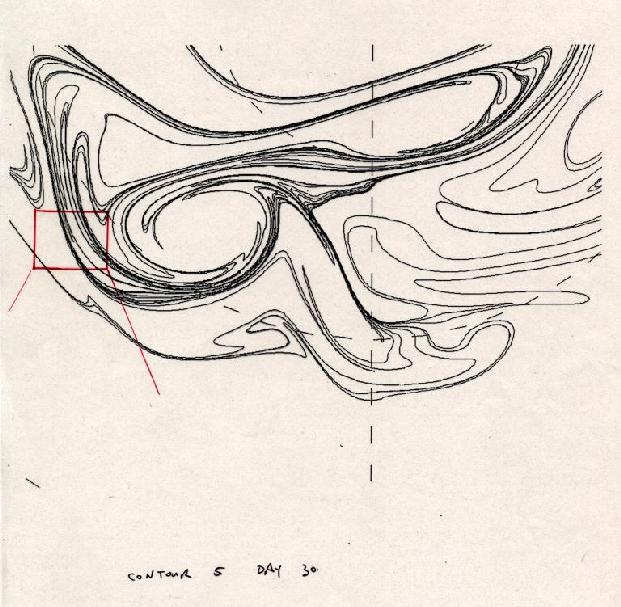
Zooming in again: this gives some feeling for just how small is the exponentially small filament scale that has been generated by this time (day 30):
Slide 8:

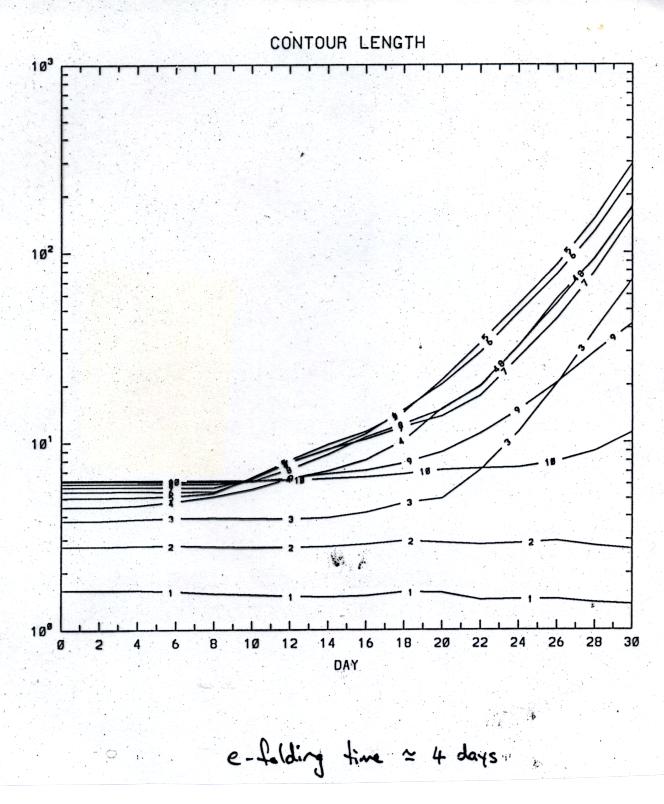
Slide 8a shows how the total length of the midlatitude contours increases exponentially fast, with e-folding time of the order of 4 days. (Again by contrast, the contours within the polar vortex, contours 1 and 2, have wavelike behaviour and do not lengthen.) Another plot from reference [2] (omitted here) shows the minimum distance between contours, i.e. the width of the thinnest filaments. This decreases even faster than the total contour length increases, with an e-folding time of the order of 1 day.
Slide 8a:
Here's a beautiful picture of stratospheric air invading the upper troposphere on the 320K isentropic surface (around jetliner cruise altitude), again computed using the contour-advection techique over a time interval of 4 days, this time with a velocity field from ECMWF's meteorological analyses [4]. It nicely shows the tendency for an advected quantity to form filaments, in the real atmosphere, on timescales of a few days. A comparison with 6 micron water-vapour images (not shown here, but see ref. [4] or [5]) suggests that the whole pattern including filaments may well be realistic:
Slide 9:
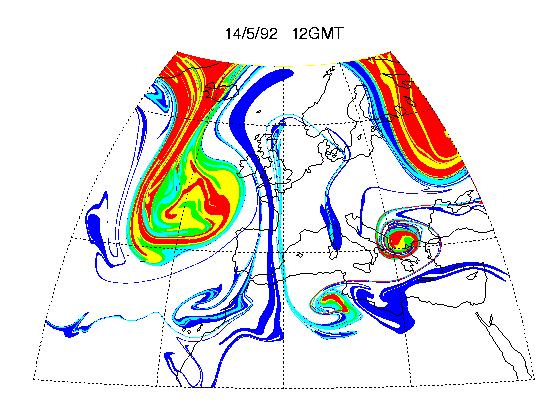
It might nevertheless be questioned whether the filaments of stratospheric air are real. How, one might ask, can such small-scale features be resolved when the resolution of the meteorological analyses is so much coarser? But the most basic point about the random-straining paradigm, and its computer realizations for realistic parameter values, is that strain fields of arbitrarily large spatial scale can produce features of arbitrarily small spatial scale, as well as doing it exponentially fast. The robustness of the process already noted argues for its ubiquity in the real world. Given that most of the features of slide 9 are echoed in the water-vapour pattern (see ref. [4] or [5]), and that filaments are an inherent part of the whole picture when advection is accurately represented, there's a strong argument that many of the filaments should be real.
Reference [3] demonstrated more systematically, and in two different ways, that there is substance to this last idea. First, it showed how a deliberate coase-graining (smoothing) of the velocity field made surprisingly little difference to filament formation. Second, it studied a case in which high-resolution chemical observations were available from NASA's ER-2 aircraft from a flight during the AASE2 campaign. When the aircraft flew across one of the filaments predicted by a contour-advection calculation, the corresponding chemical signature was seen. Other case studies (e.g. from the ASHOE campaign) have repeatedly shown by chemical observations that such predicted filaments are often real, when the meteorological analyses are more or less correct and when accurate tracer-advection computations are used. Of course what I'm calling `filaments', with their distinctive chemical signatures, are really sloping sheets or thin layers intersecting the isentropic surface. Their slopes tend to be of the order of Prandtl's ratio f/N, where f is the Coriolis parameter and N the buoyancy or Brunt-Väisälä frequency (static stability) of the stratification [6].
The ability, or potential ability, of numerical models to correctly describe small-scale features produced by advective straining is basic to the power, or potential power, of models combined with data assimilation, especially since much of the dynamics turns out to be bound up with another advected quantity, the Rossby-Ertel potential vorticity (PV). To see this we must turn to the second basic idea for this talk, that of `PV inversion'. As explained in ref. [4] we may regard slide 9 as showing, to good approximation, an isentropic distribution of PV and will use that fact below.
One among many reasons why the idea of PV inversion is important for chemistry will emerge below (in slide 18, bottom left). It is the upward `roller coaster' ride of stratospheric air parcels as they approach an upper-air blocking anticyclone, forming large-scale polar stratospheric clouds with their well-known consequences for ozone depletion.
The idea of PV inversion -- first recognized, in different ways, by Jule Charney and Ernst Kleinschmidt in the 1940s -- is crucial to understanding many aspects of the large-scale dynamics. For instance it's crucial to understanding why contours 1 and 2 in the model stratosphere above exhibit wavelike behaviour (slide 6). An animation of the flow, displayed next in low-resolution flash-shockwave format, vividly shows that the edge of the polar-vortex core has a peculiar resilience or quasi-elasticity. That, in turn, is part of why we observe a large degree of chemical isolation of the real stratospheric polar vortex core from its chemically different surroundings. The animation is from the work of reference [2], and shows PV on the left and a tracer injected into middle latitudes on the right:
[Higher-quality versions are available here as follows: real player (.rm or .ram), 4.7Mbyte, excellent quality and best quality per megabyte; quicktime (.mov), 31Mbyte, excellent quality if you have the bandwidth; podcast (.m4v), 2.9Mbyte, smallest with passable quality; mpeg 4 (.mp4), 1.2Mbyte, quality not much better than the flash-shockwave.]
The resilience or quasi-elasticity of the vortex-core edge is due to a very basic mechanism called Rossby-wave propagation, or, as I sometimes like to call it, Rossby-wave `elasticity' even though it is not like ordinary elasticity in every respect. Though very simple it seems to acquire an air of mystery in atmospheric-dynamics textbooks. That's because the role of inversion is left unstated despite its central, and crucial, role in understanding the Rossby-wave mechanism, which I'll show. (There's a `lucidity principle' that says that, in order to be intelligible, one has to be about twice as explicit as one feels necessary.) But first let's revisit the most elementary aspects of vortex dynamics.
Slide 10 summarizes the world's simplest model of vortex dynamics -- ordinary textbook 2-dimensional vortex dynamics -- in which we neglect viscosity or internal fluid friction. You might think that such a toy model couldn't be a serious model of real, 3-dimensional atmospheric vortex dynamics (polar vortex isolation, cyclones and anticyclones, Rossby-wave teleconnections, and so on). But the slide shows the equations in a form that points directly toward the generalizations to realistic stratified rotating flow. The point is that those far-reaching generalizations can be made easy to understand if we use the idea of inversion.
Slide 10:
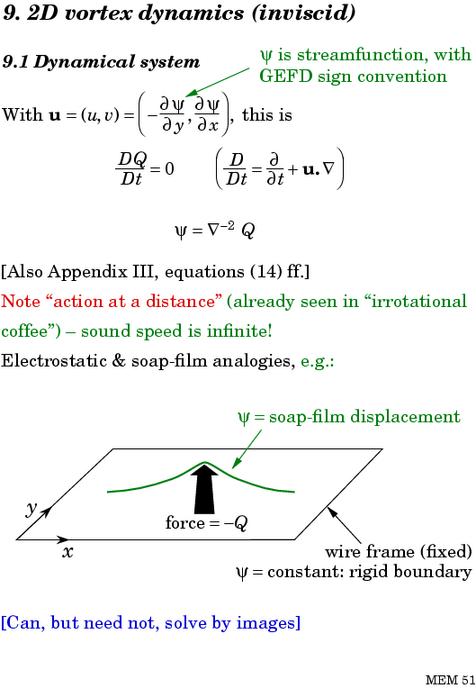
(`Appendix III' above refers to a review made available as part of the Summer School supplementary materials.)
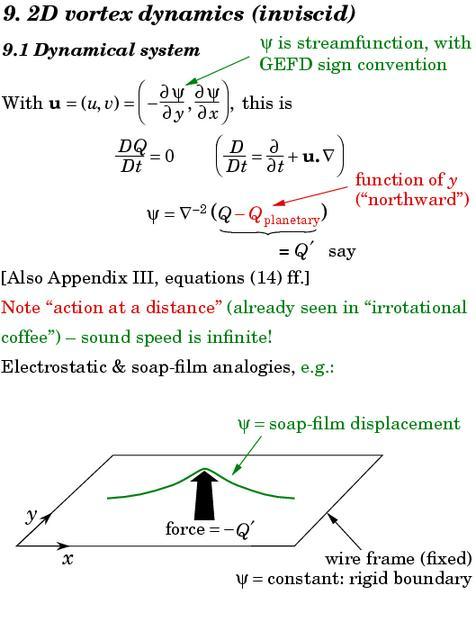
The central equation involving the inverse Laplacian says that if you know the vorticity field Q, then you can deduce everything else. This is the invertibility principle. The process of deducing everything else -- in this case the streamfunction ψ and the velocity field u -- is the computational process called inversion, more precisely inversion of the Q field to get everything else. It means that Q field contains all the dynamical information about the state of the system at any instant.
One can develop intuition about the inversion process via analogies such as electrostatics, or static soap-film or membrane shapes under a given force - Q per unit area, as suggested at the bottom of the slide. In the electrostatic analogy, the stream function or soap-film displacement ψ corresponds to the electrostatic potential due to a charge distribution - Q , and the velocity field u to the electric field with each of its vectors rotated through a right angle.
As remarked in the slide, the inversion process entails action at a distance. If I change the force field at one place on a soap film, then the static shape changes everywhere. Action at a distance is reasonable in the fluid problem, because we've assumed incompressible motion. The fluid system has an infinite speed of sound.
In the soap-film picture on slide 10 we have a concentrated force in the middle, and a surrounding structure evanescent with distance. The implied velocity field circulates clockwise around the centre, following the contours of the soap-film topography. This is nothing but the entity that we call a vortex, namely, a central vorticity anomaly Q together with the surrounding structure that goes along with it, determined by inversion. The structure really does `go along with' the central anomaly. If the anomaly is moved by some advecting flow, perhaps due to another vortex some distance away, then invertibility says that the whole structure has to stay firmly attached to the anomaly, and move along with it wherever it goes. It all makes sense -- everything, so to speak, hangs together -- as long as the velocities involved are very low in comparison with the speed of sound.
So the vortex is a bit like an atom -- the nucleus together with its surrounding structure of electronic orbitals. For an atom moving at ordinary speeds, very low in comparison with the speed of light, the Born-Oppenheimer approximation applies and tells you that the orbitals stay firmly attached to the nucleus, moving along with it wherever it goes. For a neutral atom in its ground state there's a statement closely analogous to the invertibility principle for Q, namely, that knowing the position and charge of the nucleus is enough to determine the structure of the surrounding electronic orbitals regardless of the motion of the nucleus.
(You may notice that I've been a bit cavalier about the Born-Oppenheimer approximation. What needs to be low in comparison with the speed of light is the relevant velocity scale for atomic motion divided by the fine-structure constant, where the velocity scale is that giving the acceleration of the nucleus over distances of the order of the size of the atom. But that's a fine distinction for present purposes.)
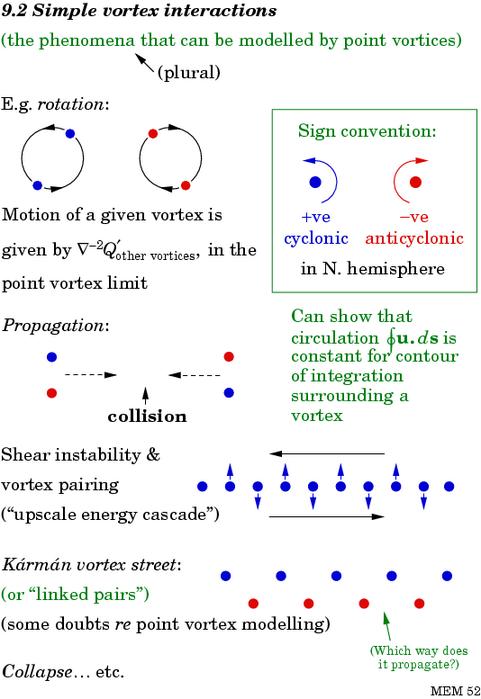
Slide 11 shows some standard examples of dynamical behaviour in the 2-D system. These are cases where the vortices are most like atoms, with their central Q anomalies, the `vortex cores', concentrated into small areas. The vortices can then be idealized as `point vortices' (Q consisting of delta functions). Only the cores are shown:
Slide 11:
Slide 12 shows, by contrast, how the top-left case in slide 11 changes for finite-sized vortex cores when the cores are close to each other. We then have a sort of `nuclear reaction' -- a `nuclear fusion' of a kind impossible for real atoms. Analogies have their limitations. The two cores are no longer resilient enough to withstand straining. They distort then merge together almost perfectly, leaving thin filaments spiralling around. (There's a beautiful conservation theorem for `angular impulse', the second radial moment of the Q distribution, that tells you that a small part of the core material must end up at a larger distance.)
Slide 12:
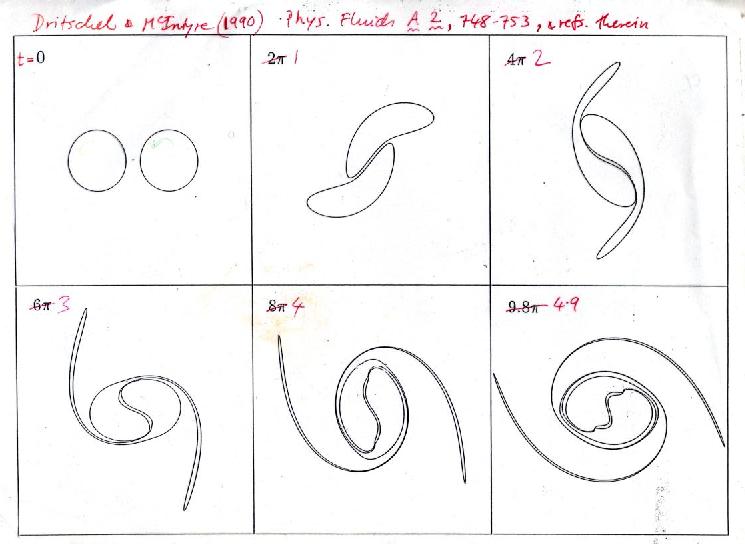
The next slide, 13, will prepare us for the simple explanation of Rossby-wave elasticity that isn't in the atmospheric-dynamics textbooks. It conveys an intuitive understanding, not restricted to idealized cases where the mathematical solutions are simple.
Slide 13 is a duplicate of slide 10 except for the addition of a background `planetary' vorticity Qplanetary(y) with a large-scale gradient. This is a toy-model representation of the large-scale potential-vorticity gradient in the real atmosphere (more detail in slide 16 below). The real gradient is due to the factor ∇θ in the formula for the PV (Rossby-Ertel potential vorticity), which takes over the role of Q in the most realistic models,
PV = { (2Ω + ∇×u) . ∇θ} / ρ ,
where ∇ is the nabla operator, (2Ω + ∇×u) is the 3-dimensional absolute vorticity vector, θ the potential temperature, and ρ the density. The factor ∇θ is a vector oriented nearly vertically, because of the atmosphere's stable stratification. So the scalar product with that factor picks out the vertical component of 2Ω, twice the absolute angular velocity vector. The vertical component of 2Ω has, of course, a large-scale gradient with respect to latitude.
Coming back to the toy model, we see from the equations in slide 13 that inversion now acts on the vorticity anomaly, where anomaly now means the departure Q´ = Q - Qplanetary from the background. This is necessary in order that the inversion process deliver what we need to know, namely the velocity field relative to the rotating Earth:
Slide 13:
Here then is how Rossby waves work. Remember that DQ/Dt = 0, i.e. that Q (including the planetary background) is advected like the mixing ratio of a chemical tracer. (This by the way is where the assumption of frictionless motion is needed. That is, it's needed for DQ/Dt = 0 to be exactly true. It's not needed for inversion.)
Slide 14 is plan view, i.e. it shows the xy plane. The green contours are contours of constant Q (including the planetary background) in a thought-experiment in which the Q contours are slightly undulated. (Remember, the Q contours are also material contours -- you can imagine them marked with green dye.) Now the moment the Q contours are undulated we have nonzero anomalies Q´ on the right of the inversion equation. These are shown by the red plus and minus signs, with circular arrows as a reminder of the sense of each anomaly, clockwise or anticlockwise.
The invertibility principle tells us that the moment we know the pattern of anomalies Q´ , we can deduce the streamfunction and the velocity field. (It is at this point that the textbooks tend to get mysterious. But there is no room for imprecision here. Soap-film shapes are soap-film shapes.)
What's most significant about the velocity field determined by inversion is the phase relation of the velocities, the blue arrows labelled `induced winds'. By a perverse convention, `induced' simply means deduced by inversion. The velocities, advecting the green material contours, are ninety degrees out of phase with the original displacements:
Slide 14:
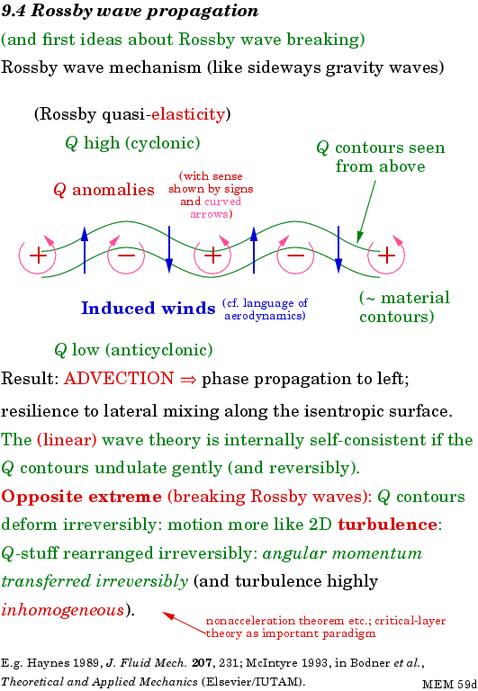
So it follows from simple kinematics, as night follows day, that the undular pattern must be propagating leftward. That's all there is to the Rossby wave-propagation mechanism! Make a movie in your mind of what the blue velocity field does to the green contours, remembering that the velocities stay ninety degrees out of phase with the displacements at all times.
The upshot is that, in a peculiar way, the green contours behave as if they were quasi-elastic in the sense that, as the waves go by, a material point on a green contour oscillates back and forth about an equilibrium position. However, it is unlike ordinary elasticity in that the undulations propagate solely to the left. A rightward propagating wave is dynamically impossible. With right-handed axes the phase propagation always has the higher background Q values on its right. We could have anticipated this one-way character of the phase propagation from the presence of only a single time derivative in the prognostic equation DQ/Dt = 0. This is quite unlike classical wave problems, in which the time derivatives always come in pairs.
(I don't have time to say much about the idea of Rossby-wave breaking, mentioned on slide 14, but it's another fundamental idea and if you're interested it's discussed in my reviews (e.g. page 24 of the abovementioned Appendix III of the supplementary material for the Summer School), and in this paper with Tim Palmer written at a time when the idea was controversial. The idea will, however, reappear in the third part of this talk, in slide 23.)
Notice that there's nothing about the argument summarized in slide 14 that requires the background Q gradient to be due solely to the Earth's rotation. You can have background Q gradients from other things such as a gradient in the mean shear. The Rossby-wave mechanism works just the same, and the next slide, 15, underlines that point in what you might think is an unexpected way.
Slide 15 shows a classical shear instability, another ubiquitous phenomenon. In this case it's simulated very accurately using the toy model of slide 10 and the contour-advection algorithm, together with an accurate numerical representation of vorticity inversion. As was pointed out in the 1960s by James Lighthill and Francis Bretherton, the instability mechanism can be most simply understood in terms of a pair of counterpropagating Rossby waves -- this time owing their existence to shear-related background Q gradients concentrated on just two material contours, with uniform Q everywhere else (pink or white in the slide -- pink is positive or anticlockwise relative to white). The two Rossby waves, one on each contour of concentrated Q gradient (pink-white material boundary), each propagate against the local mean flow and phase-lock together, with a phase shift such that each makes the other grow exponentially. The exponential growth follows kinematically from the fact that the velocities are now less than ninety degrees out of phase with the displacements. This crucial fact about the phase shift is straightforward to see from the invertibility principle, extending the argument summarized in slide 14 and adding together the velocities induced by the two rows of Q anomalies. Full details are given in the abovementioned supplementary material.
Slide 15:
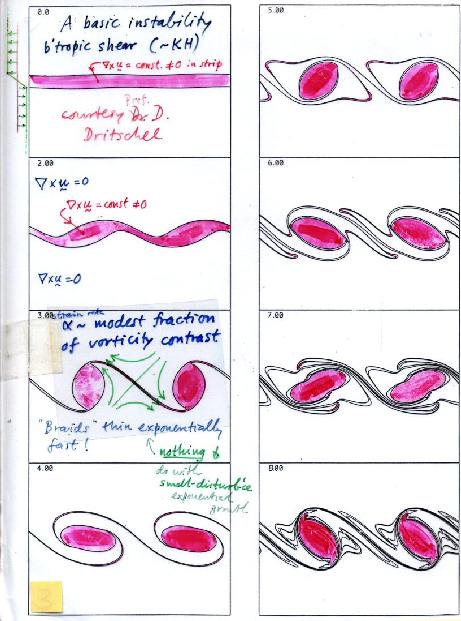
The appearance of thin braids or filaments after the unstable disturbance saturates at finite amplitude should come as no surprise! They further illustrate the first part of the talk. Apart from these, the instability has, in its typical way, given birth to a row of vortices -- which itself would be unstable, as indicated two-thirds of the way down slide 11, except that here the computation is constrained to be periodic in the x direction with period just one wavelength.
Now for the far-reaching generalizations, spelt out in full. They imply that all the qualitative insights sketched above carry over to much more realistic models of stratified, rotating fluid dynamics. In particular, we still have a single prognostic time derivative and its consequence, the one-way phase propagation of Rossby waves, with high Q on the right, where Q is now redefined as the PV and where high or low Q refers to relative values on an isentropic surface. The isentropic or constant-potential-temperature surfaces play a key role in the dynamics because they are the buoyancy surfaces of the stable stratification. They are also material surfaces if diabatic heating and cooling are negligible.
Slide 16:

As already suggested, such isentropic maps would tend, if sufficiently finely resolved, to look very much like slide 9. Of course isentropic maps of PV produced by directly using meteorological analyses or forecast fields in the above formulae can provide only a relatively coarse-grain view, though in today's state of the art they manage to capture an impressive amount of detail, even if not the finest filaments.
The two formulae for the PV in slide 16 are equivalent for practical purposes, in atmospheric dynamics, with the standard choice f(θ) = θ. The PV and its key property of being an advected quantity are implicit in the circulation theorems of Lord Kelvin and V. Bjerknes. The first derivations of explicit formulae, and demonstrations of the advective property, were published by Carl-Gustaf Rossby in 1936 and 1940. These assumed hydrostatic balance. Hans Ertel's famous 1942 paper derived the exact (non-hydrostatic) formula, the first of the two in slide 16. (I am grateful to Norman Phillips and George Platzman for historical insights. More detail can be found in my recent Encyclopedia article on potential vorticity.)
By a peculiar accident, for which there is no deep reason at all, the standard choice f(θ) = θ leads to another useful property of the PV, namely that the extratropical tropopause has a roughly constant PV value.
As regards the dynamics the only difference, relative to slides 10 and 13, is that the inversion operator is 3-dimensional, and more complicated. How to do such inversions accurately gets rather technical. In some cases of interest the accuracy can be made astonishingly high. The reasons for this are subtle and ill-understood, and very much a topic of ongoing research. `Astonishingly' means the following. The counterpart of the Born-Oppenheimer approximation is that, for the formal validity of PV inversion, fluid velocities should be low in comparison not only with the speed of sound but also with the speed of inertia-gravity waves. Any such waves can then be regarded as oscillations about a state of balanced motion, as it's called. It is to this balanced state that the invertibility principle applies. However, in practice the waves don't need to be all that fast. It is as if one had an atom that still managed to hang together in a world where the speed of light is much slower.
But the important thing is that you can still think qualitatively in terms of soap films and, in 3 dimensions, in terms of electrostatics. So qualitative arguments like that for Rossby-wave elasticity, summarized in slide 14, still hold. (Notice again from slide 16 that we still have only a single prognostic time derivative.) Counterpropagating Rossby waves can still give rise to shear instabilities, and these now include so-called `baroclinic instabilities' (Eady-Charney instabilities) due to vertical shear.
Slide 17 summarizes the essence of the foregoing:

Important technicality: The anomalies in Q that are relevant to inversion, and hence to vortex and Rossby-wave dynamics, are Q values relative to surrounding values on an isentropic surface (as revealed, for instance, by patterns like those in slide 9). That is why it's isentropic maps of PV that are dynamically relevant and not, for instance, isobaric maps [7]. As a reminder of this I like to talk about isentropic anomalies of PV.
Let's now look at some `PV atoms'. These are structures commonly found in the real atmosphere. Long before their origin was understood, meteorologists were familiar with all their characteristic features, through meticulous observation and hand analysis. They have their own zoological names, of course: cyclones and anticyclones.
Let's take another look at slide 9, duplicated below. As already mentioned, it gives an estimate of the isentropic distribution of PV on the 320K isentropic surface, around jetliner cruise altitudes, at a particular moment. Lower-stratospheric air has PV values several times higher than tropospheric air, mainly because of the higher ∇θ values (higher static stabilities) in the stratosphere. The air coloured red has estimated PV values between 5 and 6 times that of the air at the boundary of the coloured regions. Dark blue is between 1 and 2 times and light blue 2 and 3 times, values typical of the tropopause. (Maps like this remind us that the tropopause usually has a rather complicated shape!)
Slide 9 again:

Let's zoom in on the coloured blob of stratospheric air over Macedonia, which represents a positive or cyclonic isentropic anomaly of PV. If you were to take a vertical section through the middle of that anomaly, or through the larger-scale cyclonic anomaly west of France, you would see a structure similar in many respects to what's shown in the top left section in the next slide, 18, appropriately scaled. It is one of our `PV atoms', a generic upper-air cyclone computed theoretically by PV inversion.
The tropopause has a characteristic dip (bottom of red region), and intersects several of the isentropic surfaces, including the 320K isentrope. These surfaces are shown as the contours spanning the section horizontally. They are shown at intervals of 5K in potential temperature. As you move along one of the intersecting isentropes the PV increases by a factor of 6 as you enter the red region. So on each of these isentropes there is a strong positive, or cyclonic, isentropic anomaly of PV. The other set of contours in slide 18, some of them closed, give the wind speed at intevals of 3 metres per second. The wind is into the screen at the right and out at the left, and circulates around the red PV anomaly just as with our simple 2D vortices. In this example the wind has a maximum just over 20 metres/second at the tropopause. In slide 9 above, you can see filaments over the Black and Mediterranean Seas beginning to be deformed into spirals by the wind field.
The whole structure is like an atom in just the same sense as before. All the features in the section including the wind field, the tropopause dip, and, for instance, the upward bending of isentropes below the red PV anomaly and the downward bending above it, are robust features coming out of the PV inversion. Now look at the bottom left section, which shows the same set of features, but all of them in the reverse sense. This is an upper-air blocking anticyclone. You'd see something like this over Norway in the case of slide 9, even though it's not yet a fully developed anticyclone. The red region now marks a negative isentropic anomaly of PV. The upward bending of the stratospheric isentropes (smudgy orange mark) guides the `roller-coaster tracks' for large-scale polar-stratospheric-cloud formation; see notes on slide. (Sorry the slide's such a mess, but perhaps there's some historical interest here.)
Slide 18:
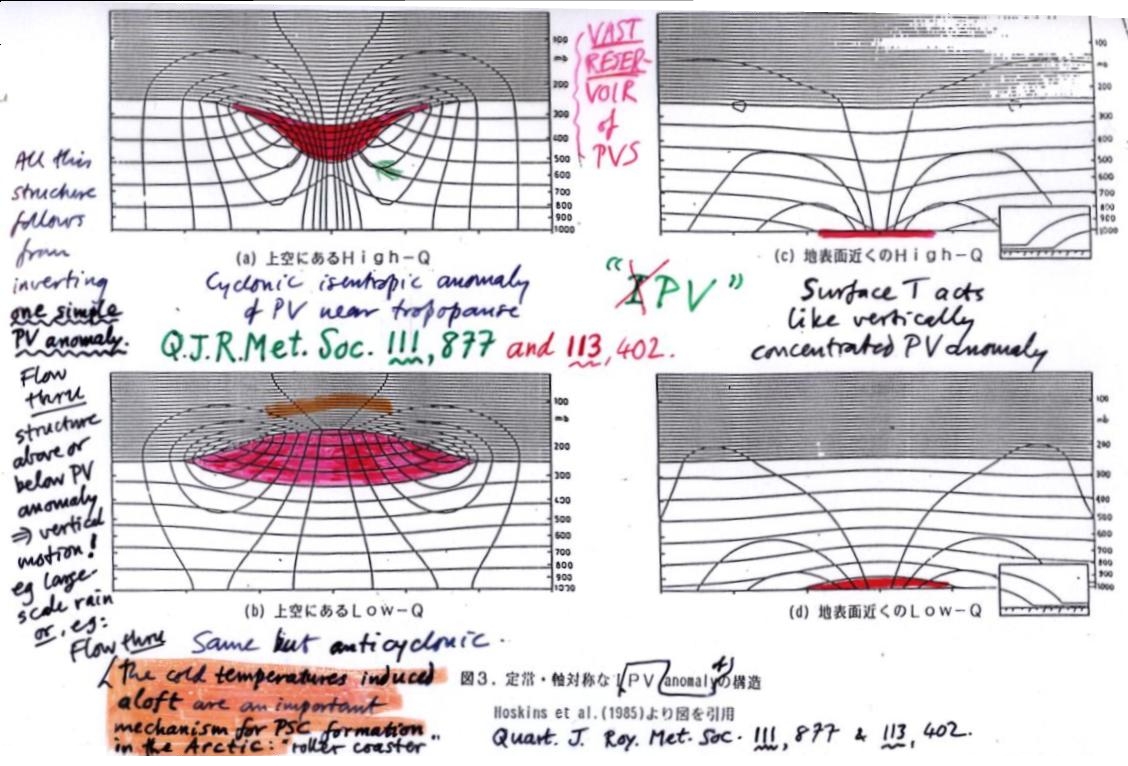
The two examples on the right illustrate the fact, crucially important for tropospheric weather developments, that surface temperature anomalies are equivalent to vertically concentrated PV anomalies, with warm anomalies cyclonic (top right panel) and cold anticyclonic (bottom right panel). Such cases, and their implications for cyclogenesis and other weather developments, are extensively discussed in ref. [7]. All the inversion calculations shown in slide 18 were kindly provided by Professor Alan Thorpe.
Of course you can have more complicated structures; it is here that the analogy with atoms gets a bit shaky. There's no counterpart of quantization to keep things simple! Inevitably, the shapes of the PV anomalies are more complicated in some cases; for instance cyclonic upper-air PV anomalies may develop extrusions along the intersecting isentropes, called tropopause folds or upper-air fronts, adjacent to the nearby tropopause wind maximum.
The last two slides in this part of the talk (which I didn't have time to show) are just the Summer School material recalling the basics of conservation relations. This bears on some remarks in slide 16, about `PV substance' or `PV charge'. The points are elementary, but there has been some confusion in the literature about how they apply to PV and its analogy with a chemical mixing ratio. If you see phrases like `PVS', `PV substance', or `PVC' -- not polyvinyl chloride but `PV charge' -- watch out! Such phrases are sometimes used in a sense very different from that in phrases like `water substance' or `electric charge'. Similar warnings are necessary regarding the words `source', `sink', `budget', and `transport'. A detailed and comprehensive discussion is available in Section 11, p. 36ff. of the same Appendix III as before. These are just matters of conceptual clarity but they still have some importance, it seems to me, as background to the coming effort in simultaneous dynamical and chemical data assimilation.
Slide 19:
Slide 20:

There has been an enormous, though gradual, paradigm change over the past century regarding the fluid dynamics of global-scale atmospheric circulations. The first clue came from the work of the young Harold Jeffreys at the UK Met Office early in the century. Then things became clearer, bit by bit, as more observational data became available after the second world war, with key contributions from Victor Starr and co-workers in the 1950s at MIT and then, roughly in historical order, from Arnt Eliassen and Enok Palm at Oslo, Jule Charney and Phil Drazin at MIT, Colin Hines at Toronto, Francis Bretherton at Cambridge, Jim Holton and Mike Wallace at Seattle, Dick Lindzen at NCAR and Harvard, Bob Dickinson at MIT and NCAR, John Houghton at Oxford, Keith Stewartson at University College, London, Tom and Helen Warn at Montreal, and Alan Plumb at CSIRO, Melbourne, Australia. The old paradigm, famously promoted by Albert Defant in 1921, was to view the atmosphere as a large Reynolds number fluid system subject to a turbulent eddy viscosity. That was a perfectly natural idea when contemplating the chaotic eddying of cyclones and anticyclones. The new paradigm is to recognize the atmosphere as, nevertheless, dominated on the global scale by radiation stress. This is the far less conspicuous, yet all-pervasive, momentum and angular momentum transport due to a subtle but persistent dynamical organization of fluctuations by fluid-dynamical wave propagation mechanisms. We may sum it up in the form of an aphorism: as far as the momentum budget is concerned `there's no such thing as turbulence without waves'.
Of course the atmosphere-ocean system as a whole is ultimately driven by solar heating, but I am talking about the internal mechanisms that drive global-scale mean circulations such as the stratospheric Brewer-Dobson circulation.
The new paradigm has excellent credentials since it not only solved the problem of the Brewer-Dobson circulation -- a problem originally noted by Alan Brewer in his pioneering 1949 paper on the dryness of the stratosphere -- but it also easily solved what used to be considered three of the great enigmas of atmospheric science. Ref. [1] sketches some of the history. The three enigmas were
The dynamical organization of fluctuations, with systematic mean effects, is one of the grand themes of physics. If you want another example you need look no further than your right arm. Pick up a book and hold it aloft. What is happening? Clever molecular motors in your muscle fibres are organizing the thermal fluctuations, with systematic mean effects! (That's why life as we know it can exist only in a certain range of temperatures.)
What's important in the case of the atmosphere is that the mere presence of a wave propagation mechanism of any kind tends, by its very nature, to impose some organization on the fluctuating fields, in the form of systematic correlations among the different variables. There is always such a tendency even when the fluctuations are complicated and chaotic. If, for instance, there is a systematic correlation between fluctuations in the zonal and vertical velocity components, then this can give rise to a systematic vertical transport of angular momentum. (The idea is simple enough -- but embedding it into a self-consistent, causally coherent and quantitative framework is not trivial, especially as regards the role of wave generation and dissipation. It's here that the theoretical contributions of Eliassen, Palm, Charney, Drazin, Bretherton, and Dickinson were seminal, along with an earlier insight going back to Rayleigh's Theory of Sound, namely the constraint imposed by Kelvin's circulation theorem on problems of this kind. Those contributions were important precedents to my own work with David Andrews, Tim Dunkerton, Flossie Hsu and Oliver Bühler on Lagrangian means, nonacceleration theorems, PV-theta coordinates and the so-called `transformed Eulerian-mean (TEM)' framework. That work and the work of Stewartson, Warn and Warn on so-called `Rossby-wave critical layers' led in turn to a sharpened understanding -- developed in collaboration with Peter Killworth, Peter Haynes, and last but not least Tim Palmer -- of the nature and generic significance of wave breaking in a suitably defined sense, for all the diverse wave types involved. I'll illustrate that significance shortly, in an extremely simple way, using the toy model of slide 13.)
The atmosphere, being stably stratified and subject to strong Coriolis effects, has plenty of fluid-dynamical wave propagation mechanisms at its disposal. Especially with the lower-frequency waves -- Rossby and inertia-gravity, and the various hybrid types -- the wave-mediated momentum transport is powerful enough, on average, to be dominant on large spatial scales. Eddy viscosity or turbulent friction is a short-range momentum transport process, such as one has within the atmospheric boundary layer. By contrast, wave-mediated momentum transport is a long-range process, limited only by the distances over which the waves can propagate, e.g. from the Earth's surface into the high stratosphere and beyond.
One consequence of this long-range character is that the idea of eddy viscosity makes no sense.
It makes no sense even when the fluctuations are more or less chaotic, what a dynamical-systems expert might call `turbulent'. Indeed, it's commonplace for radiation-stress-dominated systems to exhibit what Victor Starr called `negative viscosity'. I prefer, however, to call it `anti-friction', in order to avoid any association with the mathematical pathology and conceptual absurdity of negative or infinite diffusion coefficients. (The QBO routinely provides examples of both.) Anti-frictional behaviour simply means that the dynamically-organized fluctuations tend to drive the system away from solid rotation. A viscosity or internal friction, which is simply a diffusivity of momentum, would do the opposite. It would drive the system toward solid rotation.
The world's simplest demonstration of these anti-frictional effects is the celebrated Plumb-McEwan experiment. This is a laboratory counterpart of the atmospheric QBO:
Slide 21:
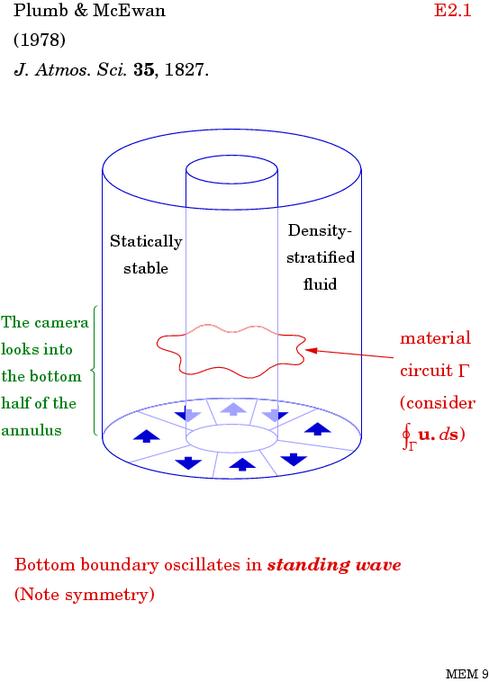
The system is driven away from solid rotation by nothing more than the fluctuations imposed by the bottom boundary, which is a flexible membrane made to oscillate in a standing wave. The fluctuations get dynamically organized by the stable stratification, through the internal gravity wave propagation mechanism. A movie of what happens, plus a description of the easiest way to repeat the experiment, is available at this excellent website. You can also find it by googling QBO "Tech Tips". The experiment is mirror-symmetric, but as pointed out by Alan Plumb in the 1970s it exhibits spontaneous symmetry-breaking. It spontaneously develops a mean flow around the annulus.
The mean flow reverses quasi-periodically, with a spatiotemporal pattern qualitatively like that of the real QBO. At all times there is at least one downward-moving extremum, more often two extrema, in the vertical profile of mean angular velocity. You can always take the quotient of eddy momentum flux over mean shear and say that that's the eddy viscosity by definition. But then at an extremum we have zero mean shear and infinite eddy viscosity. Between two extrema we have negative eddy viscosity. More to the point, though, there's no local functional relation between eddy momentum flux and mean shear, and there's no pathological, anti-diffusive behaviour. The system is driven away from solid rotation, but only by a finite amount. In fact the range of mean angular velocities lies in between the positive and negative angular phase speeds of the imposed fluctuations. In technical jargon, there are `no critical levels' in this case.
We know from extensive modelling studies that practically any boundary motion with a broad spectrum of angular phase speeds will have much the same antifrictional effect. Having merely two phase speeds, as in the original experiment, is sufficient but not necessary. (You can demonstrate this for yourself with a hands-on model of the QBO available as part of the computer demonstrations from our Summer School website.) The QBO in the real atmosphere is almost certainly driven by a complicated spectrum of fluctuations involving several different wave types. That the real QBO is wave-driven can be said with extremely high confidence, despite there still being gaps in our knowledge of which wave types are the most important [10]. That confidence depends on the scientific history in an interesting way. It illustrates what I call the `Michelson-Morley principle', the importance of negative results in science; see ref. [1], sections 7-8.
I have no time to do justice here either to the Michelson-Morley principle or to the third enigma, the cold summer polar mesopause -- the story of noctilucent clouds, the miners' canary, and related matters -- except to say that the cold mesopause has turned out to be another case of the dynamical organization of fluctuations by the internal gravity wave mechanism. The circumstances are different from those of slide 21, because of the dynamical differences between the tropics and the extratropics [8] together with the radiative conditions near solstice. The history of ideas is rather convoluted. There were notable contributions from, again roughly in historical order, Colin Hines, Francis Bretherton, John Houghton, Dick Lindzen, Jim Holton, Rolando Garcia and Susan Solomon, again underpinned by the insight from Rayleigh's Theory of Sound even though sound waves, as such, don't contribute significantly.
But what about the Brewer-Dobson circulation? And what about global-scale atmospheric circulations in general? What about the first enigma, regarding chaotic fluctuations on synoptic weather scales and larger? In the closing pages of the famous 1967 monograph by Edward N. Lorenz [11], this problem was flagged as ``the most important problem in general-circulation theory'' that lacks even ``a fairly adequate qualitative explanation''. Early clues as to its likely solution came especially from the 1969 work of Bob Dickinson [13], though it subsequently emerged [14] that Eric Eady had independently seen the point some years earlier (and, characteristically, hadn't bothered to publish it). With 20-20 hindsight it's now clear that the key to all these problems is absurdly simple. It's the single time derivative appearing in the dynamical system of slide 17, with its implications for the properties of Rossby waves.
Consider first the Brewer-Dobson circulation. Here's the well-known plot I usually show to illustrate the circulation, from ref. [9], with a qualitative indication of the single-cell mesospheric Murgatroyd-Singleton circulation sketched in above it. The quantitative part of the plot, nicely showing the TEM mass-transport streamlines of the Brewer-Dobson circulation, is based on an excellent homogeneous dataset from the LIMS satellite. Sorry the slide has grown a bit busy over the years. It's for January 1979, close to solstice:
Slide 22:
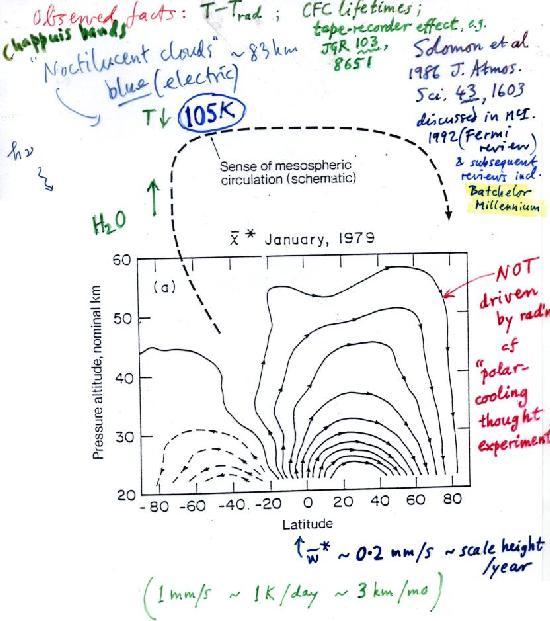
It's worth emphasizing the high scientific confidence we have in this picture, at least in its main qualitative features. The whole picture has been confirmed and cross-checked in many ways, including the `tape-recorder effect' [12] discovered after the Upper Atmosphere Research Satellite was launched in 1991. The seasonal cycle of tropical tropopause dryness is imprinted on the rising branch of the Brewer-Dobson circulation, just like the signal on a magnetic tape. This gives us a completely independent estimate of the `tape speed', typically about a scale height per year at the bottom of the picture.
Now the first point to make is that the Brewer-Dobson circulation is not driven by solar heating. Indeed, the oft-repeated myth that it's so driven never made sense. Insolation maximizes at the summer pole at solstice, so why isn't the rising branch over the summer pole at all altitudes? I suspect that the myth might have come from looking at equations of the type A = B where A represents ascent and B the diabatic heating rate, and unconsciously assuming that B causes A. (Sir James Jeans' cautionary example is A = room temperature, B = thermometer temperature.)
Careful modelling studies have shown that the circulation is driven mainly by the angular momentum transport produced by breaking Rossby waves, through a mechanical pumping action that depends on the Coriolis effect. Let's call it `gyroscopic pumping' for brevity. One might also call it the `motor' of the notional `tape recorder'. The pumping action tightly controls the total mass flux through each Brewer-Dobson cell. This in turn, together with ultraviolet actinic flux distributions and surf-zone mixing (recall the animation following slides 5-8), controls chemical characteristics like the age and age-spectrum of stratospheric air.
So, in particular, we can now explain the location of the rising branch over the tropics as largely due to the characteristics of the Rossby-wave-driven gyroscopic pump or `tape-recorder motor'. The precise location and distribution of tropical upwelling feels, in addition, a slight latitudinal nudging back and forth from the seasonal cycle of solar heating. This hardly influences the total mass flux and so has an effect more like that of latitudinally-shifting guidance wheels, or rollers, that nudge the rising `tape' northward or southward without changing its `speed', more precisely its mass flux.
The pump acts against thermal radiative relaxation. Where it pushes air downward, temperatures are pushed above radiative equilibrium. Where it pulls air upward, as in the tropical tropopause layer, temperatures are pulled below radiative equilibrium.
Indeed, it is precisely on this effect that mass-flux estimates like that of slide 22 are based, since they are derived from remotely-sensed stratospheric temperatures, together with a radiation scheme with cloud and surface-temperature estimates to compute the difference between observed and radiative-equilibrium temperatures.
Thanks to today's space-based remote sensing technology, which can sense many chemical tracers as well as temperatures, you can even see the gyroscopic pump in action in the real stratosphere, in some detail. But how does this mechanical pump work? Why does it drive the circulation in the sense shown? As far as the stratosphere is concerned the answer, as already emphasized, lies mainly in the properties of Rossby waves. There are two parts to the answer, first the force field due to Rossby-wave-mediated radiation stress, and second the atmosphere's response to that force field.
When Rossby waves break or otherwise dissipate, there is a wave-mediated flux of angular momentum (in technical jargon, an `Eliassen-Palm flux') that systematically transports negative (westward, retrograde) angular momentum from the altitudes and latitudes where the waves are generated, mostly in the massive troposphere beneath, to the altitudes and latitudes where they're being dissipated. Consequently the dissipation region feels a persistent retrograde force, F say. This one-signedness or ratchet-like character of the force F is a further conseqence of the single time derivative in slide 17 as well as being, of course, another variation on our generic theme, the dynamical organization of fluctuations.
This ratchet effect can be demonstrated in an unbelievably simple way with the 2D toy model from slide 13, as follows.
The key points are first that breaking Rossby waves mix PV along the isentropes, tending to homogenize its isentropic distribution in a mid-latitude `surf zone', as illustrated in slides 5-8 above, and second that the inversion to get the resulting change δu(y) in the zonally averaged velocity profile u(y) -- a trivial calculation in the toy model -- shows at once that such mixing produces a deficit of zonal momentum in or near that zone. That is, the mixing produces an effect equivalent to a retrograde force F. Details for the toy-model calculation are shown in the following slide, in which the left-hand graph sketches, in idealized form, the zonally averaged Q(y) profile before and after mixing. The profile before mixing is simply Qplanetary = constant + βy (dashed line), where β is a positive constant (Rossby's beta-plane approximation). The middle graph is for an actual model calculation, courtesy of Peter Haynes, using the equations from slide 13 and building on the work of Stewartson, Warn and Warn. The right-hand graph (red hatching) is the resulting δu(y). The thumbnail sketches summarize the inversion to get δu(y):
Slide 23:
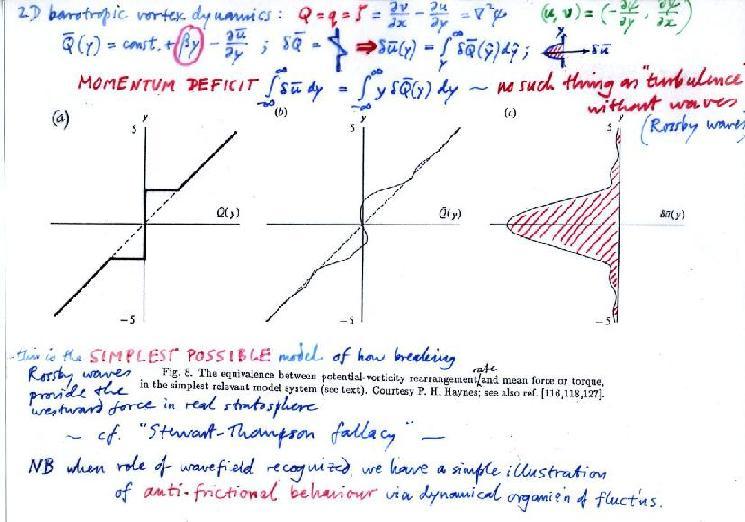
In the toy model, the Rossby waves that break in the surf zone come from outside the region shown, from the positive y side. This well illustrates the aphorism that `there's no such thing as turbulence without waves'. Without the presence of a wave-induced momentum flux from outside, the formation of the surf zone would lead to a gross contradiction, namely a momentum deficit mysteriously appearing from nowhere and violating angular momentum conservation.
In the toy-model example the sign of the wave-mediated momentum flux turns out to be anti-frictional. That's the essence of the solution to the first enigma, the case of anti-frictional behaviour discovered by Jeffreys and Starr. In that case the Rossby-wave surf zone is roughly speaking in the tropical upper troposphere and lower stratosphere, in a layer that includes the tropical tropopause layer, in the ballpark of 350-400K. The region of what Starr called `negative viscosity' is in the subtropics just poleward of, and somewhat beneath, that surf zone.
For the purposes of this discussion, the toy-model results are extremely robust. The mixing may be perfect or imperfect. Essentially the same results are obtained from a hierarchy of increasingly realistic models [2], [7], [15], [16], [17]. Ref. [15] shows that the retrograde force F arises in a realistic stratospheric model in essentially the same way as in our toy model. The example discussed in refs. [7], [16], and [17], the Simmons-Hoskins LC1 baroclinic wave life cycle, is a realistic simulation of extratropical cyclogenesis of a typical kind. It exhibits precisely the kind of anti-frictional effect noted by Starr and shows that that effect arises from Rossby-wave propagation and breaking, in just the same way as in the toy model.
By that fact, the example provides another powerful illustration of the aphorism that `there's no such thing as turbulence without waves'. The discovery [17] that Rossby-wave propagation and breaking of the kind in question is essential to the LC1 picture was a huge surprise at the time (1980). At first sight we were dealing with nothing but typical elements of `the chaotic eddying of cyclones and anticyclones', complete with all their familiar features such as occluding surface fronts. Of course it had long been known that the early exponential growth stage of the precursor baroclinic instability can be understood in terms of counterpropagating Rossby waves, as already mentioned in connection with slide 15. The surprise came when ref. [17] stumbled on the first evidence, from spatiotemporal Eliassen-Palm flux patterns, that the nonlinear, occluding stage launches another Rossby wave that propagates upward and equatorward (this of course involves group velocity rather than phase velocity) and behaves just like the Rossby wave in the toy model.
Let's now get back to the case of the Brewer-Dobson circulation and the surf zones involved in driving it [15]. In the summer cell on the left the Rossby waves penetrate diffractively from below and do not get very far into the stratosphere. But they still break and produce a surf zone, over a broad latitude range, kinematically favoured by the summertime zonal wind distribution. In the winter cell the Rossby waves penetrate much higher (Charney-Drazin effect). At most stratospheric altitudes the surf zone due to their breaking is centred on middle latitudes, and looks very like the model surf zone seen in slides 5-8 and in the animation above. Indeed the remotely-sensed animation that I previously dubbed `the gyroscopic pump in action' shows the real surf zone in the mid-to-upper stratosphere. (Note the different map projection; slides 5-8 are polar stereographic.) The distinction between the polar vortex and the surf zone is very clear from the behaviour of the material contours (e.g. slide 6), such as contours 1 and 2 in the polar vortex, undulating under the influence of Rossby-wave elasticity, and their opposite extreme, contour 5 well inside the surf zone, which deforms irreversibly. For reasons connected with Kelvin's circulation theorem such irreversible deformation, of otherwise wavy contours, is taken as the generic defining characteristic of wave breaking.
Now the toy-model calculation of slide 23 and its qualitative confirmation in more realistic calculations like that of ref. [15] have already told us that, in any surf zone where Rossby waves break persistently -- mixing isentropic distributions of PV and thus weakening its large-scale latitudinal gradients along isentropes, in competition with the thermal relaxation that tries to restore those gradients -- the effect on the zonally averaged dynamics is robustly equivalent to a persistent retrograde force F. So we need to understand the extratropical response to such a force.
Imagine such a force acting on the zonally-averaged dynamics, as suggested in slide 24:
Slide 24:
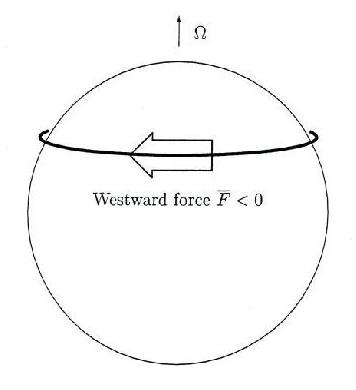
This is now about zonally averaged, hence zonally symmetric, dynamics. So we can picture what the equations say by thinking of a notional ring of air that feels the force F, i.e. is persistently being pushed westwards.
Now for this purpose the Earth is a rapidly rotating planet. With realistic parameter values the inverse Coriolis parameter defines a much shorter timescale than the timescale of the response to the force F. Therefore Coriolis effects are very strong. The air pushed westwards tries persistently to turn poleward. This is a mechanical pumping action, what I have been calling gyroscopic pumping. The response to such pumping has been very thoroughly studied by modellers, both numerically and analytically [8].
It is instructive to neglect seasonal variation and perform a thought-experiment in which the force F, regarded as given, is switched on in a thermally-relaxational atmosphere in a steady thermal environment, `perpetual January' if you will. An interesting feature of the response is the so-called `downward control' property. To fix ideas let us imagine the force F switched on over some range of extratropical latitudes and in some layer between, say, altitudes z1 and z2 and then left on. The gyroscopically-pumped meridional circulation burrows downward below the forcing layer until it reaches the Earth's surface, where it closes off in a frictional boundary layer [8] and settles toward a steady state in which there is no meridional circulation above the forcing layer. The steady state is approached fastest for broad F distributions over a large range of latitudes -- usually, for practical purposes, somewhat faster than seasonal timescales. Ref. [8] gives a careful analysis and discussion of timescales and their relation to latitudinal scale, Coriolis and buoyancy times f -1, N -1, and radiative relaxation times. Of course the phrase `downward control' refers only to the meridional circulation gyroscopically pumped by the given F, in this particular thought-experiment. In the real atmosphere there's plenty of upward influence, not least via the upward diffraction or propagation of the Rossby waves that give rise to the force F.
On the global scale of slide 22, we may take the steady-state scenario as approximately correct in January. So we may legitimately think of the observed Brewer-Dobson ascent or descent at a given altitude as mainly driven by gyroscopic pumping from above. This in turn has implications for the current debates about the web of causal linkages, particularly upward and downward influence in the real troposphere-stratosphere system.
So there it is. To finish, let me show two slides that summarize and slightly extend some of what I've said. Slide 25 tries to summarize the implications of wintertime stratospheric surf-zone structure, including the Rossby-elastic, shear-enhanced `eddy-transport barriers' at the subpolar and subtropical edges of the winter surf zone. Slide 26 recalls the partial analogy between such eddy-transport barriers and their counterparts due to ordinary stratification, or gravity-wave elasticity, such as the vertical trapping of pollutants by an atmospheric boundary-layer-capping `temperature inversion' or strongly stratified layer. That analogy is echoed in certain theoretical developments, including a beautiful analogy between the available potential energy associated with vertical undulations in the stratified layer on the one hand, and the conservable `Rossby-wave activity' associated with the sideways undulations of PV contours depicted in slide 14, and related to the Eliassen-Palm flux. But that would take a whole further lecture...
Slide 25:
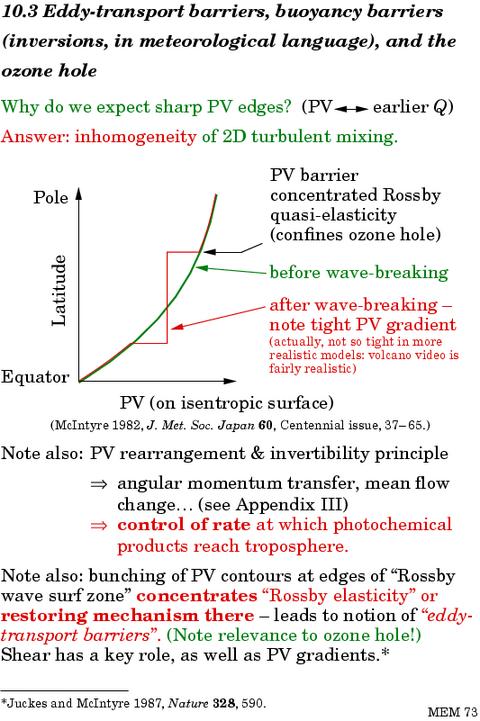
Slide 26:

I thank ECMWF for kindly inviting me to participate in this interdisciplinary seminar, also NERC for its sponsorship of past Summer Schools over the past 15 years, and the University of Toronto for its invitation to give the Noble Lectures in April 2005, all of which have greatly stimulated the development of this material. Drs Robert Hunt, Mark Hallworth, Björn Haßler, and Adrian Cullum-Hanshaw provided generous help with the graphics. Dr Warwick Norton kindly gave permission to use the animation introducing the section on PV inversion.
[1] McIntyre, M. E., 2003: On global-scale atmospheric circulations. In: Perspectives in Fluid Dynamics: A Collective Introduction to Current Research, ed. G. K. Batchelor, H. K. Moffatt, M. G. Worster; Cambridge, University Press, 631 pp., 557-624. Paperback edition with corrections.
[2] Norton, W. A., 1994: Breaking Rossby waves in a model stratosphere diagnosed by a vortex-following coordinate system and a technique for advecting material contours. J. Atmos. Sci., 51, 654-673.
[3] Waugh, D. W., Plumb, R. A., 1994: Contour advection with surgery: a technique for investigating finescale structure in tracer transport. J. Atmos. Sci., 51, 530-540.
[4] Appenzeller, C., Davies, H. C., Norton, W. A., 1996: Fragmentation of stratospheric intrusions. J. Geophys. Res., 101, 1435-1456.
[5] Holton, J. R., et al, 1995: Stratosphere-troposphere exchange. Revs. Geophys., 33, 403-439.
[6] Haynes, P. H., Anglade, J., 1997: The vertical-scale cascade of atmospheric tracers due to large-scale differential advection. J. Atmos. Sci., 54, 1121-1136.
[7] Hoskins, B. J., et al., 1985: On the use and significance of isentropic potential-vorticity maps. Q. J. Roy. Meteorol. Soc., 111, 877-946. Also Corrigendum 113, 402-404.
[8] Haynes, P. H., et al., 1991: On the ``downward control'' of extratropical diabatic circulations by eddy-induced mean zonal forces. J. Atmos. Sci., 48, 651-678. Also 53, 2105-2107 and Haynes, P. H., 1998: The latitudinal structure of the quasi-biennial oscillation, Q. J. Roy. Meteorol. Soc., 124, 2645-2670.
[9] Solomon, S., et al., 1986: Tracer transport by the diabatic circulation deduced from satellite observations. J. Atmos. Sci., 43, 1603-1617.
[10] Baldwin, M. P., et al., 2001: The quasi-biennial oscillation. Revs. Geophys., 39, 179-229.
[11] Lorenz, E. N., 1967: The Nature and Theory of the General Circulation of the Atmosphere. Geneva, World Meteorol. Org., 161pp. See pp. 149-151.
[12] Mote, P. W., et al., 1998: Vertical velocity, vertical diffusion, and dilution by midlatitude air in the tropical lower stratosphere. J. Geophys. Res., 103, 8651-8666 (also refs. therein).
[13] Dickinson, R. E., 1969: Theory of planetary wave-zonal flow interaction. J. Atmos. Sci., 26, 73-81.
[14] Green, J. S. A., 1970: Transfer properties of the large-scale eddies and the general circulation of the atmosphere. Q. J. Roy. Meteorol. Soc., 96, 157-185.
[15] Robinson, W. A., 1988: Analysis of LIMS data by potential vorticity inversion. J. Atmos. Sci., 45, 2319-2342.
[16] Thorncroft, C., et al., 1993: Two paradigms of baroclinic-wave life-cycle behaviour. Q. J. Roy. Meteorol. Soc., 119, 17-55.
[17] Edmon, H. J., et al., 1980: Eliassen-Palm cross-sections for the troposphere. J. Atmos. Sci., 37, 2600-2616. Also Corrigendum, J. Atmos. Sci., 38, 1115, especially second last item.
Back to my home page, http://www.damtp.cam.ac.uk/user/mem/