1 The Fundamentals of Statistical Mechanics 3 Quantum Gases

2 Classical Gases

Our goal in this section is to use the techniques of statistical mechanics to describe the dynamics of the simplest system: a gas. This means a bunch of particles, flying around in a box. Although much of the last section was formulated in the language of quantum mechanics, here we will revert back to classical mechanics. Nonetheless, a recurrent theme will be that the quantum world is never far behind: we’ll see several puzzles, both theoretical and experimental, which can only truly be resolved by turning on $\hbar$ .

2.1 The Classical Partition Function

For most of this section we will work in the canonical ensemble. We start by reformulating the idea of a partition function in classical mechanics. We’ll consider a simple system – a single particle of mass $m$ moving in three dimensions in a potential $V(\vec{q})$ . The classical Hamiltonian of the system³³ 3 If you haven’t taken the Classical Dynamics course, you should think of the Hamiltonian as the energy of the system expressed in terms of the position and momentum of the particle. is the sum of kinetic and potential energy,

\displaystyle H=\frac{\vec{p}^{2}}{2m}+V(\vec{q})

We earlier defined the partition function (1.21) to be the sum over all quantum states of the system. Here we want to do something similar. In classical mechanics, the state of a system is determined by a point in phase space. We must specify both the position and momentum of each of the particles — only then do we have enough information to figure out what the system will do for all times in the future. This motivates the definition of the partition function for a single classical particle as the integration over phase space,

\displaystyle Z_{1}=\frac{1}{h^{3}}\int d^{3}qd^{3}p\ e^{-\beta H(p,q)}

(2.49)

The only slightly odd thing is the factor of $1/h^{3}$ that sits out front. It is a quantity that needs to be there simply on dimensional grounds: $Z$ should be dimensionless so $h$ must have dimension $({\rm length}\times{\rm momentum})$ or, equivalently, Joules-seconds $(Js)$ . The actual value of $h$ won’t matter for any physical observable, like heat capacity, because we always take $\log Z$ and then differentiate. Despite this, there is actually a correct value for $h$ : it is Planck’s constant, $h=2\pi\hbar\approx 6.6\times 10^{-34}\ Js$ .

It is very strange to see Planck’s constant in a formula that is supposed to be classical. What’s it doing there? In fact, it is a vestigial object, like the male nipple. It is redundant, serving only as a reminder of where we came from. And the classical world came from the quantum.

2.1.1 From Quantum to Classical

It is possible to derive the classical partition function (2.49) directly from the quantum partition function (1.21) without resorting to hand-waving. It will also show us why the factor of $1/h$ sits outside the partition function. The derivation is a little tedious, but worth seeing. (Similar techniques are useful in later courses when you first meet the path integral). To make life easier, let’s consider a single particle moving in one spatial dimension. It has position operator $\hat{q}$ , momentum operator $\hat{p}$ and Hamiltonian,

\displaystyle\hat{H}=\frac{\hat{p}{}^{2}}{2m}+V(\hat{q})

If $|n\rangle$ is the energy eigenstate with energy $E_{n}$ , the quantum partition function is

\displaystyle Z_{1}=\sum_{n}e^{-\beta E_{n}}=\sum_{n}\ \langle n|e^{-\beta\hat% {H}}|n\rangle

(2.50)

In what follows, we’ll make liberal use of the fact that we can insert the identity operator anywhere in this expression. Identity operators can be constructed by summing over any complete basis of states. We’ll need two such constructions, using the position eigenvectors $|q\rangle$ and the momentum eigenvectors $|p\rangle$ ,

\displaystyle{\bf 1}=\int dq\,|q\rangle\langle q|\ \ \ \ ,\ \ \ \ \ {\bf 1}=% \int dp\ |p\rangle\langle p|

We start by inserting two copies of the identity built from position eigenstates,

	$\displaystyle Z_{1}$	$\displaystyle=$	$\displaystyle\sum_{n}\langle n\|\int dq\,\|q\rangle\langle q\|e^{-\beta\hat{H}}% \int\,dq^{\prime}\|q^{\prime}\rangle\langle q^{\prime}\|n\rangle$
		$\displaystyle=$	$\displaystyle\int dqdq^{\prime}\,\langle q\|e^{-\beta\hat{H}}\|q^{\prime}\rangle% \,\sum_{n}\langle q^{\prime}\|n\rangle\langle n\|q\rangle$

But now we can replace $\sum_{n}|n\rangle\langle n|$ with the identity matrix and use the fact that $\langle q^{\prime}|q\rangle=\delta(q^{\prime}-q)$ , to get

\displaystyle Z_{1}=\int dq\,\langle q|e^{-\beta\hat{H}}|q\rangle

(2.51)

We see that the result is to replace the sum over energy eigenstates in (2.50) with a sum (or integral) over position eigenstates in (2.51). If you wanted, you could play the same game and get the sum over any complete basis of eigenstates of your choosing. As an aside, this means that we can write the partition function in a basis independent fashion as

\displaystyle Z_{1}=\rm Tr\,e^{-\beta\hat{H}}

So far, our manipulations could have been done for any quantum system. Now we want to use the fact that we are taking the classical limit. This comes about when we try to factorize $e^{-\beta\hat{H}}$ into a momentum term and a position term. The trouble is that this isn’t always possible when there are matrices (or operators) in the exponent. Recall that,

\displaystyle e^{\hat{A}}e^{\hat{B}}=e^{\hat{A}+\hat{B}+{\textstyle\frac{1}{2}% }[\hat{A},\hat{B}]+\ldots}

For us $[\hat{q},\hat{p}]=i\hbar$ . This means that if we’re willing to neglect terms of order $\hbar$ — which is the meaning of taking the classical limit — then we can write

\displaystyle e^{-\beta\hat{H}}=e^{-\beta\hat{p}^{2}/2m}\,e^{-\beta V(\hat{q})% }+{\cal O}(\hbar)

We can now start to replace some of the operators in the exponent, like $V(\hat{q})$ , with functions $V(q)$ . (The notational difference is subtle, but important, in the expressions below!),

$\displaystyle Z_{1}$	$\displaystyle=$	$\displaystyle\int dq\,\langle q\|e^{-\beta\hat{p}^{2}/2m}e^{-\beta V(\hat{q})}\|q\rangle$
	$\displaystyle=$	$\displaystyle\int dq\,e^{-\beta V(q)}\langle q\|e^{-\beta\hat{p}^{2}/2m}\|q\rangle$
	$\displaystyle=$	$\displaystyle\int dqdpdp^{\prime}e^{-\beta V(q)}\langle q\|p\rangle\langle p\|e^% {-\beta\hat{p}^{2}/2m}\|p^{\prime}\rangle\langle p^{\prime}\|q\rangle$
	$\displaystyle=$	$\displaystyle\frac{1}{2\pi\hbar}\int dqdp\,e^{-\beta H(p,q)}$

where, in the final line, we’ve used the identity

\displaystyle\langle q|p\rangle=\frac{1}{\sqrt{2\pi\hbar}}e^{ipq/\hbar}

This completes the derivation.

2.2 Ideal Gas

The first classical gas that we’ll consider consists of $N$ particles trapped inside a box of volume $V$ . The gas is “ideal”. This simply means that the particles do not interact with each other. For now, we’ll also assume that the particles have no internal structure, so no rotational or vibrational degrees of freedom. This situation is usually referred to as the monatomic ideal gas. The Hamiltonian for each particle is simply the kinetic energy,

\displaystyle H=\frac{\vec{p}^{\,2}}{2m}

And the partition function for a single particle is

\displaystyle Z_{1}(V,T)=\frac{1}{(2\pi\hbar)^{3}}\int d^{3}qd^{3}p\,e^{-\beta% \vec{p}^{\,2}/2m}

(2.52)

The integral over position is now trivial and gives $\int d^{3}q=V$ , the volume of the box. The integral over momentum is also straightforward since it factorizes into separate integrals over $p_{x}$ , $p_{y}$ and $p_{z}$ , each of which is a Gaussian of the form,

\displaystyle\int dx\,e^{-ax^{2}}=\sqrt{\frac{\pi}{a}}

So we have

\displaystyle Z_{1}=V\left(\frac{mk_{B}T}{2\pi\hbar^{2}}\right)^{3/2}

We’ll meet the combination of factors in the brackets a lot in what follows, so it is useful to give it a name. We’ll write

\displaystyle Z_{1}=\frac{V}{\lambda^{3}}

(2.53)

The quantity $\lambda$ goes by the name of the thermal de Broglie wavelength,

\displaystyle\lambda=\sqrt{\frac{2\pi\hbar^{2}}{mk_{B}T}}

(2.54)

$\lambda$ has the dimensions of length. We will see later that you can think of $\lambda$ as something like the average de Broglie wavelength of a particle at temperature $T$ . Notice that it is a quantum object – it has an $\hbar$ sitting in it – so we expect that it will drop out of any genuinely classical quantity that we compute. The partition function itself (2.53) is counting the number of these thermal wavelengths that we can fit into volume $V$ .

Figure 8: Deviations from ideal gas law at sensible densities

Deviations from ideal gas law at extreme densities — Figure 8: Deviations from ideal gas law at sensible densities

$Z_{1}$ is the partition function for a single particle. We have $N$ , non-interacting, particles in the box so the partition function of the whole system is

\displaystyle Z(N,V,T)=Z_{1}^{N}=\frac{V^{N}}{\lambda^{3N}}

(2.55)

(Full disclosure: there’s a slightly subtle point that we’re brushing under the carpet here and this equation isn’t quite right. This won’t affect our immediate discussion and we’ll explain the issue in more detail in Section 2.2.3.)

Armed with the partition function $Z$ , we can happily calculate anything that we like. Let’s start with the pressure, which can be extracted from the partition function by first computing the free energy (1.36) and then using (1.35). We have

$\displaystyle p$	$\displaystyle=$	$\displaystyle-\frac{\partial{F}}{\partial{V}}$	(2.56)
	$\displaystyle=$	$\displaystyle\frac{\partial}{\partial V}(k_{B}T\log Z)$
	$\displaystyle=$	$\displaystyle\frac{Nk_{B}T}{V}$

This equation is an old friend – it is the ideal gas law, $pV=Nk_{B}T$ , that we all met in kindergarten. Notice that the thermal wavelength $\lambda$ has indeed disappeared from the discussion as expected. Equations of this form, which link pressure, volume and temperature, are called equations of state. We will meet many throughout this course.

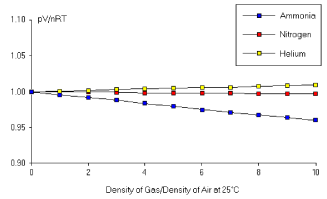
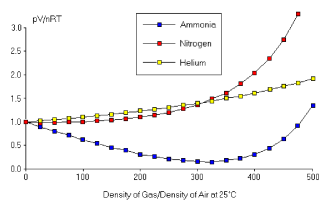
As the plots above show⁴⁴ 4 Both figures are taken from the web textbook “General Chemistry” and credited to John Hutchinson., the ideal gas law is an extremely good description of gases at low densities. Gases deviate from this ideal behaviour as the densities increase and the interactions between atoms becomes important. We will see how this comes about from the viewpoint of microscopic forces in Section 2.5.

It is worth pointing out that this derivation should calm any lingering fears that you had about the definition of temperature given in (1.7). The object that we call $T$ really does coincide with the familiar notion of temperature applied to gases. But the key property of the temperature is that if two systems are in equilibrium then they have the same $T$ . That’s enough to ensure that equation (1.7) is the right definition of temperature for all systems because we can always put any system in equilibrium with an ideal gas.

2.2.1 Equipartition of Energy

The partition function (2.55) has more in store for us. We can compute the average energy of the ideal gas,

\displaystyle E=-\frac{\partial}{\partial\beta}\log Z=\frac{3}{2}Nk_{B}T

(2.57)

There’s an important, general lesson lurking in this formula. To highlight this, it is worth repeating our analysis for an ideal gas in arbitrary number of spatial dimensions, $D$ . A simple generalization of the calculations above shows that

\displaystyle Z=\frac{V^{N}}{\lambda^{DN}}\ \ \ \ \ \Rightarrow\ \ \ \ \ \ \ E% =\frac{D}{2}Nk_{B}T

Each particle has $D$ degrees of freedom (because it can move in one of $D$ spatial directions). And each particle contributes ${\textstyle\frac{1}{2}}Dk_{B}T$ towards the average energy. This is a general rule of thumb, which holds for all classical systems: the average energy of each free degree of freedom in a system at temperature $T$ is ${\textstyle\frac{1}{2}}k_{B}T$ . This is called the equipartition of energy. As stated, it holds only for degrees of freedom in the absence of a potential. (There is a modified version if you include a potential). Moreover, it holds only for classical systems or quantum systems at suitably high temperatures.

We can use the result above to see why the thermal de Broglie wavelength (2.54) can be thought of as roughly equal to the average de Broglie wavelength of a particle. Equating the average energy (2.57) to the kinetic energy $E=p^{2}/2m$ tells us that the average (root mean square) momentum carried by each particle is $p\sim\sqrt{mk_{B}T}$ . In quantum mechanics, the de Broglie wavelength of a particle is $\lambda_{dB}=h/p$ , which (up to numerical factors of $2$ and $\pi$ ) agrees with our formula (2.54).

Finally, returning to the reality of $d=3$ dimensions, we can compute the heat capacity for a monatomic ideal gas. It is

\displaystyle C_{V}=\left.\frac{\partial{E}}{\partial{T}}\right|_{V}=\frac{3}{% 2}Nk_{B}

(2.58)

2.2.2 The Sociological Meaning of Boltzmann’s Constant

We introduced Boltzmann’s constant $k_{B}$ in our original the definition of entropy (1.2). It has the value,

\displaystyle k_{B}=1.381\times 10^{-23}\ JK^{-1}

In some sense, there is no deep physical meaning to Boltzmann’s constant. It is merely a conversion factor that allows us to go between temperature and energy, as reflected in (1.7). It is necessary to include it in the equations only for historical reasons: our ancestors didn’t realise that temperature and energy were closely related and measured them in different units.

Nonetheless, we could ask why does $k_{B}$ have the value above? It doesn’t seem a particularly natural number. The reason is that both the units of temperature (Kelvin) and energy (Joule) are picked to reflect the conditions of human life. In the everyday world around us, measurements of temperature and energy involve fairly ordinary numbers: room temperature is roughly $300\,K$ ; the energy required to lift an apple back up to the top of the tree is a few Joules. Similarly, in an everyday setting, all the measurable quantities — $p$ , $V$ and $T$ — in the ideal gas equation are fairly normal numbers when measured in SI units. The only way this can be true is if the combination $Nk_{B}$ is a fairly ordinary number, of order one. In other words the number of atoms must be huge,

\displaystyle N\sim 10^{23}

(2.59)

This then is the real meaning of the value of Boltzmann’s constant: atoms are small.

It’s worth stressing this point. Atoms aren’t just small: they’re really really small. $10^{23}$ is an astonishingly large number. The number of grains of sand in all the beaches in the world is around $10^{18}$ . The number of stars in our galaxy is about $10^{11}$ . The number of stars in the entire visible Universe is probably around $10^{22}$ . And yet the number of water molecules in a cup of tea is more than $10^{23}$ .

Chemist Notation

While we’re talking about the size of atoms, it is probably worth reminding you of the notation used by chemists. They too want to work with numbers of order one. For this reason, they define a mole to be the number of atoms in one gram of Hydrogen. (Actually, it is the number of atoms in 12 grams of Carbon-12, but this is roughly the same thing). The mass of Hydrogen is $1.6\times 10^{-27}\ Kg$ , so the number of atoms in a mole is Avogadro’s number,

\displaystyle N_{A}\approx 6\times 10^{23}

The number of moles in our gas is then $n=N/N_{A}$ and the ideal gas law can be written as

\displaystyle pV=nRT

where $R=N_{A}k_{B}$ is the called the Universal gas constant. Its value is a nice sensible number with no silly power in the exponent: $R\approx 8\ JK^{-1}{\rm mol}^{-1}$ .

2.2.3 Entropy and Gibbs’s Paradox

“It has always been believed that Gibbs’s paradox embodied profound thought. That it was intimately linked up with something so important and entirely new could hardly have been foreseen.”

Erwin Schrödinger

We said earlier that the formula for the partition function (2.55) isn’t quite right. What did we miss? We actually missed a subtle point from quantum mechanics: quantum particles are indistinguishable. If we take two identical atoms and swap their positions, this doesn’t give us a new state of the system – it is the same state that we had before. (Up to a sign that depends on whether the atoms are bosons or fermions – we’ll discuss this aspect in more detail in Sections 3.5 and 3.6). However, we haven’t taken this into account – we wrote the expression $Z=Z_{1}^{N}$ which would be true if all the $N$ particles in the were distinguishable — for example, if each of the particles were of a different type. But this naive partition function overcounts the number of states in the system when we’re dealing with indistinguishable particles.

It is a simple matter to write down the partition function for $N$ indistinguishable particles. We simply need to divide by the number of ways to permute the particles. In other words, for the ideal gas the partition function is

\displaystyle Z_{\rm ideal}(N,V,T)=\frac{1}{N!}Z_{1}^{N}=\frac{V^{N}}{N!% \lambda^{3N}}

(2.60)

The extra factor of $N!$ doesn’t change the calculations of pressure or energy since, for each, we had to differentiate $\log Z$ and any overall factor drops out. However, it does change the entropy since this is given by,

\displaystyle S=\frac{\partial}{\partial T}(k_{B}T\log Z_{\rm ideal})

which includes a factor of $\log Z$ without any derivative. Of course, since the entropy is counting the number of underlying microstates, we would expect it to know about whether particles are distinguishable or indistinguishable. Using the correct partition function (2.60) and Stirling’s formula, the entropy of an ideal gas is given by,

\displaystyle S=Nk_{B}\left[\log\left(\frac{V}{N\lambda^{3}}\right)+\frac{5}{2% }\right]

(2.61)

This result is known as the Sackur-Tetrode equation. Notice that not only is the entropy sensitive to the indistinguishability of the particles, but it also depends on $\lambda$ . However, the entropy is not directly measurable classically. We can only measure entropy differences by the integrating the heat capacity as in (1.10).

The benefit of adding an extra factor of $N!$ was noticed before the advent of quantum mechanics by Gibbs. He was motivated by the change in entropy of mixing between two gases. Suppose that we have two different gases, say red and blue. Each has the same number of particles $N$ and sits in a volume V, separated by a partition. When the partition is removed the gases mix and we expect the entropy to increase. But if the gases are of the same type, removing the partition shouldn’t change the macroscopic state of the gas. So why should the entropy increase? This is referred to as the Gibb’s paradox. Including the factor of $N!$ in the partition function ensures that the entropy does not increase when identical atoms are mixed⁵⁵ 5 Be warned however: a closer look shows that the Gibbs paradox is rather toothless and, in the classical world, there is no real necessity to add the $N!$ . A clear discussion of these issues can be found in E.T. Jaynes’ article “The Gibbs Paradox” which you can download from the course website.

2.2.4 The Ideal Gas in the Grand Canonical Ensemble

It is worth briefly looking at the ideal gas in the grand canonical ensemble. Recall that in such an ensemble, the gas is free to exchange both energy and particles with the outside reservoir. You could think of the system as some fixed subvolume inside a much larger gas. If there are no walls to define this subvolume then particles, and hence energy, can happily move in and out. We can ask how many particles will, on average, be inside this volume and what fluctuations in particle number will occur. More importantly, we can also start to gain some intuition for this strange quantity called the chemical potential, $\mu$ .

The grand partition function (1.39) for the ideal gas is

\displaystyle{\cal Z}_{\rm ideal}(\mu,V,T)=\sum_{N=0}^{\infty}e^{\beta\mu N}Z_% {\rm ideal}(N,V,T)=\exp\left(\frac{e^{\beta\mu}V}{\lambda^{3}}\right)

From this we can determine the average particle number,

\displaystyle N=\frac{1}{\beta}\frac{\partial}{\partial\mu}\log{\cal Z}=\frac{% e^{\beta\mu}V}{\lambda^{3}}

Which, rearranging, gives

\displaystyle\mu=k_{B}T\log\left(\frac{\lambda^{3}N}{V}\right)

(2.62)

If $\lambda^{3}<V/N$ then the chemical potential is negative. Recall that $\lambda$ is roughly the average de Broglie wavelength of each particle, while $V/N$ is the average volume taken up by each particle. But whenever the de Broglie wavelength of particles becomes comparable to the inter-particle separation, then quantum effects become important. In other words, to trust our classical calculation of the ideal gas, we must have $\lambda^{3}\ll V/N$ and, correspondingly, $\mu<0$ .

At first sight, it is slightly strange that $\mu$ is negative. When we introduced $\mu$ in Section 1.4.1, we said that it should be thought of as the energy cost of adding an extra particle to the system. Surely that energy should be positive! To see why this isn’t the case, we should look more closely at the definition. From the energy variation (1.38), we have

\displaystyle\mu=\left.\frac{\partial{E}}{\partial{N}}\right|_{S,V}

So the chemical potential should be thought of as the energy cost of adding an extra particle at fixed entropy and volume. But adding a particle will give more ways to share the energy around and so increase the entropy. If we insist on keeping the entropy fixed, then we will need to reduce the energy when we add an extra particle. This is why we have $\mu<0$ for the classical ideal gas.

There are situations where $\mu>0$ . This can occur if we have a suitably strong repulsive interaction between particles so that there’s a large energy cost associated to throwing in one extra. We also have $\mu>0$ for fermion systems at low temperatures as we will see in Section 3.6.

We can also compute the fluctuation in the particle number,

\displaystyle\Delta N^{2}=\frac{1}{\beta^{2}}\frac{\partial^{2}}{\partial\mu^{% 2}}\log{\cal Z}_{\rm ideal}=N

As promised in Section 1.4.1, the relative fluctuations $\Delta N/\langle N\rangle=1/\sqrt{N}$ are vanishingly small in the thermodynamic $N\rightarrow\infty$ limit.

Finally, it is very easy to compute the equation of state in the grand canonical ensemble because (1.45) and (1.48) tell us that

\displaystyle pV=k_{B}T\log{\cal Z}=k_{B}T\frac{e^{\beta\mu}V}{\lambda^{3}}=k_% {B}TN

(2.63)

which gives us back the ideal gas law.

2.3 Maxwell Distribution

Figure 10: Maxwell distribution for Noble gases:

H e

N e

A r

and

X e

Our discussion above focusses on understanding macroscopic properties of the gas such as pressure or heat capacity. But we can also use the methods of statistical mechanics to get a better handle on the microscopic properties of the gas. Like everything else, the information is hidden in the partition function. Let’s return to the form of the single particle partition function (2.52) before we do the integrals. We’ll still do the trivial spatial integral $\int d^{3}q=V$ , but we’ll hold off on the momentum integral and instead change variables from momentum to velocity, $\vec{p}=m\vec{v}$ . Then the single particle partition function is

\displaystyle Z_{1}=\frac{m^{3}V}{(2\pi\hbar)^{3}}\int d^{3}v\,e^{-\beta m\vec% {v}^{2}/2}=\frac{4\pi m^{3}V}{(2\pi\hbar)^{3}}\int dv\,v^{2}e^{-\beta mv^{2}/2}

We can compare this to the original definition of the partition function: the sum over states of the probability of that state. But here too, the partition function is written as a sum, now over speeds. The integrand must therefore have the interpretation as the probability distribution over speeds. The probability that the atom has speed between $v$ and $v+dv$ is

\displaystyle f(v)dv={\cal N}v^{2}e^{-mv^{2}/2k_{B}T}\,dv

(2.64)

where the normalization factor ${\cal N}$ can be determined by insisting that probabilities sum to one, $\int_{0}^{\infty}f(v)\,dv=1$ , which gives

\displaystyle{\cal N}=4\pi\left(\frac{m}{2\pi k_{B}T}\right)^{3/2}

This is the Maxwell distribution. It is sometimes called the Maxwell-Boltzmann distribution. Figure 10 shows this distribution for a variety of gases with different masses at the same temperature, from the slow heavy Xenon (purple) to light, fast Helium (blue). We can use it to determine various average properties of the speeds of atoms in a gas. For example, the mean square speed is

\displaystyle\langle v^{2}\rangle=\int_{0}^{\infty}dv\ v^{2}f(v)=\frac{3k_{B}T% }{m}

This is in agreement with the equipartition of energy: the average kinetic energy of the gas is $E={\textstyle\frac{1}{2}}m\langle v^{2}\rangle={\textstyle\frac{3}{2}}k_{B}T$ .

Maxwell’s Argument

The above derivation tells us the distribution of velocities in a non-interacting gas of particles. Remarkably, the Maxwell distribution also holds in the presence of any interactions. In fact, Maxwell’s original derivation of the distribution makes no reference to any properties of the gas. It is very slick!

Let’s first think about the distribution of velocities in the $x$ direction; we’ll call this distribution $\phi(v_{x})$ . Rotational symmetry means that we must have the same distribution of velocities in both the $y$ and $z$ directions. However, rotational invariance also requires that the full distribution can’t depend on the direction of the velocity; it can only depend on the speed $v=\sqrt{v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}$ . This means that we need to find functions $F(v)$ and $\phi(v_{x})$ such that

\displaystyle F(v)\,dv_{x}dv_{y}dv_{z}=\phi(v_{x})\phi(v_{y})\phi(v_{z})\,dv_{% x}dv_{y}dv_{z}

It doesn’t look as if we possibly have enough information to solve this equation for both $F$ and $\phi$ . But, remarkably, there is only one solution. The only function which satisfies this equation is

\displaystyle\phi(v_{x})=Ae^{-Bv_{x}^{2}}

for some constants $A$ and $B$ . Thus the distribution over speeds must be

\displaystyle F(v)\,dv_{x}dv_{y}dv_{z}=4\pi v^{2}F(v)\,dv=4\pi A^{3}v^{2}e^{-% Bv^{2}}dv

We see that the functional form of the distribution arises from rotational invariance alone. To determine the coefficient $B=m/2k_{B}T$ we need the more elaborate techniques of statistical mechanics that we saw above. (In fact, one can derive it just from equipartition of energy).

2.3.1 A History of Kinetic Theory

The name kinetic theory refers to the understanding the properties of gases through their underlying atomic constituents. The discussion given above barely scratches the surface of this important subject.

Kinetic theory traces its origin to the work of Daniel Bernoulli in 1738. He was the first to argue that the phenomenon that we call pressure is due to the constant bombardment of tiny atoms. His calculation is straightforward. Consider a cubic box with sides of length $L$ . Suppose that an atom travelling with momentum $v_{x}$ in the $x$ direction bounces elastically off a wall so that it returns with velocity $-v_{x}$ . The particle experiences a change in momentum is $\Delta p_{x}=2mv_{x}$ . Since the particle is trapped in a box, it will next hit the wall at a time $\Delta t=2L/v_{x}$ later. This means that the force on the wall due to this atom is

\displaystyle F=\frac{\Delta p_{x}}{\Delta t}=\frac{mv_{x}^{2}}{L}

Summing over all the atoms which hit the wall, the force is

\displaystyle F=\frac{Nm\langle{v}_{x}^{2}\rangle}{L}

where $\langle v_{x}^{2}\rangle$ is the average velocity in the $x$ -direction. Using the same argument as we gave in Maxwell’s derivation above, we must have $\langle{v}_{x}^{2}\rangle=\langle{v^{2}}\rangle/3$ . Thus $F=Nm\langle{v}\rangle^{2}/3L$ and the pressure, which is force per area, is given be

\displaystyle p=\frac{Nm\langle{v^{2}}\rangle}{3L^{3}}=\frac{Nm\langle v^{2}% \rangle}{3V}

If this equation is compared to the ideal gas law (which, at the time, had only experimental basis) one concludes that the phenomenon of temperature must arise from the kinetic energy of the gas. Or, more precisely, one finds the equipartition result that we derived previously: ${\textstyle\frac{1}{2}}m\langle v^{2}\rangle={\textstyle\frac{3}{2}}k_{B}T$ .

After Bernoulli’s pioneering work, kinetic theory languished. No one really knew what to do with his observation nor how to test the underlying atomic hypothesis. Over the next century, Bernouilli’s result was independently rediscovered by a number of people, all of whom were ignored by the scientific community. One of the more interesting attempts was by John Waterson, a Scottish engineer and naval instructor working for the East India Company in Bombay. Waterson was considered a crackpot. His 1843 paper was rejected by the Royal Society as “nothing but nonsense” and he wrote up his results in a self-published book with the wonderfully crackpot title “Thoughts on Mental Functions”.

The results of Bernouilli and Waterson finally became accepted only after they were re-rediscovered by more established scientists, most notably Rudolph Clausius who, in 1857, extended these ideas to rotating and vibrating molecules. Soon afterwards, in 1859, Maxwell gave the derivation of the distribution of velocities that we saw above. This is often cited as the first statistical law of physics. But Maxwell was able to take things further. He used kinetic theory to derive the first genuinely new prediction of the atomic hypothesis: that the viscosity of a gas is independent of its density. Maxwell himself wrote,

”Such a consequence of the mathematical theory is very startling and the only experiment I have met with on the subject does not seem to confirm it.”

Maxwell decided to rectify the situation. With help from his wife, he spent several years constructing an experimental apparatus in his attic which was capable of providing the first accurate measurements of viscosity of gases⁶⁶ 6 You can see the original apparatus down the road in the corridor of the Cavendish lab. Or, if you don’t fancy the walk, you can simply click here:
http://www-outreach.phy.cam.ac.uk/camphy/museum/area1/exhibit1.htm. His surprising theoretical prediction was confirmed by his own experiment.

There are many further developments in kinetic theory which we will not cover in this course. Perhaps the most important is the Boltzmann equation. This describes the evolution of a particle’s probability distribution in position and momentum space as it collides with other particles. Stationary, unchanging, solutions bring you back to the Maxwell-Boltzmann distribution, but the equation also provides a framework to go beyond the equilibrium description of a gas. You can read about this in the lecture notes on Kinetic Theory.

2.4 Diatomic Gas

“I must now say something about these internal motions, because the greatest difficulty which the kinetic theory of gases has yet encountered belongs to this part of the subject”.

James Clerk Maxwell, 1875

Consider a molecule that consists of two atoms in a bound state. We’ll construct a very simple physicist’s model of this molecule: two masses attached to a spring. As well as the translational degrees of freedom, there are two further ways in which the molecule can move

•

Rotation: the molecule can rotate rigidly about the two axes perpendicular to the axis of symmetry, with moment of inertia $I$ . (For now, we will neglect the rotation about the axis of symmetry. It has very low moment of inertia which will ultimately mean that it is unimportant).
•

Vibration: the molecule can oscillate along the axis of symmetry

We’ll work under the assumption that the rotation and vibration modes are independent. In this case, the partition function for a single molecule factorises into the product of the translation partition function $Z_{\rm trans}$ that we have already calculated (2.53) and the rotational and vibrational contributions,

\displaystyle Z_{1}=Z_{\rm trans}Z_{\rm rot}Z_{\rm vib}

We will now deal with $Z_{\rm rot}$ and $Z_{\rm vib}$ in turn.

Rotation

The Lagrangian for the rotational degrees of freedom is⁷⁷ 7 See, for example, Section 3.6 of the lecture notes on Classical Dynamics

\displaystyle L_{\rm rot}=\frac{1}{2}I(\dot{\theta}^{2}+\sin^{2}\theta\dot{% \phi}^{2})

(2.65)

The conjugate momenta are therefore

\displaystyle p_{\theta}=\frac{\partial{L_{\rm rot}}}{\partial{\dot{\theta}}}=% I\dot{\theta}\ \ \ ,\ \ \ \ p_{\phi}=\frac{\partial{L_{\rm rot}}}{\partial{% \dot{\phi}}}=I\sin^{2}\theta\,\dot{\phi}

from which we get the Hamiltonian for the rotating diatomic molecule,

\displaystyle H_{\rm rot}=\dot{\theta}p_{\theta}+\dot{\phi}p_{\phi}-L=\frac{p_% {\theta}^{2}}{2I}+\frac{p_{\phi}^{2}}{2I\sin^{2}\theta}

(2.66)

The rotational contribution to the partition function is then

$\displaystyle Z_{\rm rot}$	$\displaystyle=$	$\displaystyle\frac{1}{(2\pi\hbar)^{2}}\int d\theta d\phi dp_{\theta}dp_{\phi}% \,e^{-\beta H_{\rm rot}}$	(2.67)
	$\displaystyle=$	$\displaystyle\frac{1}{(2\pi\hbar)^{2}}\sqrt{\frac{2\pi I}{\beta}}\int_{0}^{\pi% }d\theta\,\sqrt{\frac{2\pi I\sin^{2}\theta}{\beta}}\int_{0}^{2\pi}d\phi$
	$\displaystyle=$	$\displaystyle\frac{2Ik_{B}T}{\hbar^{2}}$

From this we can compute the average rotational energy of each molecule,

\displaystyle E_{\rm rot}=k_{B}T

If we now include the translational contribution (2.53), the partition function for a diatomic molecule that can spin and move, but can’t vibrate, is given by $Z_{1}=Z_{\rm trans}Z_{\rm rot}\sim(k_{B}T)^{5/2}$ , and the partition function for a gas of these object $Z=Z_{1}^{N}/N!$ , from which we compute the energy $E={\textstyle\frac{5}{2}}Nk_{B}T$ and the heat capacity,

\displaystyle C_{V}=\frac{5}{2}k_{B}N

In fact we can derive this result simply from equipartition of energy: there are 3 translational modes and 2 rotational modes, giving a contribution of $5N\times{\textstyle\frac{1}{2}}k_{B}T$ to the energy.

Vibrations

The Hamiltonian for the vibrating mode is simply a harmonic oscillator. We’ll denote the displacement away from the equilibrium position by $\zeta$ . The molecule vibrates with some frequency $\omega$ which is determined by the strength of the atomic bond. The Hamiltonian is then

\displaystyle H_{\rm vib}=\frac{p_{\zeta}^{2}}{2m}+\frac{1}{2}m\omega^{2}\zeta% ^{2}

from which we can compute the partition function

\displaystyle Z_{\rm vib}=\frac{1}{2\pi\hbar}\int d\zeta dp_{\zeta}e^{-\beta H% _{\rm vib}}=\frac{k_{B}T}{\hbar\omega}

(2.68)

The average vibrational energy of each molecule is now

\displaystyle E_{\rm vib}=k_{B}T

(You may have anticipated ${\textstyle\frac{1}{2}}k_{B}T$ since the harmonic oscillator has just a single degree of freedom, but equipartition works slightly differently when there is a potential energy. You will see another example on the problem sheet from which it is simple to deduce the general form).

Figure 11: The heat capacity of Hydrogen gas

H_{2}

. The graph was created by P. Eyland.

Putting together all the ingredients, the contributions from translational motion, rotation and vibration give the heat capacity

\displaystyle C_{V}=\frac{7}{2}Nk_{B}

This result depends on neither the moment of inertia, $I$ , nor the stiffness of the molecular bond, $\omega$ . A molecule with large $I$ will simply spin more slowly so that the average rotational kinetic energy is $k_{B}T$ ; a molecule attached by a stiff spring with high $\omega$ will vibrate with smaller amplitude so that the average vibrational energy is $k_{B}T$ . This ensures that the heat capacity is constant.

Great! So the heat capacity of a diatomic gas is ${\textstyle\frac{7}{2}}Nk_{B}$ . Except it’s not! An idealised graph of the heat capacity for $H_{2}$ , the simplest diatomic gas, is shown in Figure 11. At suitably high temperatures, around $5000K$ , we do see the full heat capacity that we expect. But at low temperatures, the heat capacity is that of monatomic gas. And, in the middle, it seems to rotate, but not vibrate. What’s going on? Towards the end of the nineteenth century, scientists were increasingly bewildered about this behaviour.

What’s missing in the discussion above is something very important: $\hbar$ . The successive freezing out of vibrational and rotational modes as the temperature is lowered is a quantum effect. In fact, this behaviour of the heat capacities of gases was the first time that quantum mechanics revealed itself in experiment. We’re used to thinking of quantum mechanics as being relevant on small scales, yet here we see that affects the physics of gases at temperatures of $2000\,K$ . But then, that is the theme of this course: how the microscopic determines the macroscopic. We will return to the diatomic gas in Section 3.4 and understand its heat capacity including the relevant quantum effects.

2.5 Interacting Gas

Until now, we’ve only discussed free systems; particles moving around unaware of each other. Now we’re going to turn on interactions. Here things get much more interesting. And much more difficult. Many of the most important unsolved problems in physics are to do with the interactions between large number of particles. Here we’ll be gentle. We’ll describe a simple approximation scheme that will allow us to begin to understand the effects of interactions between particles.

We’ll focus once more on the monatomic gas. The ideal gas law is exact in the limit of no interactions between atoms. This is a good approximation when the density of atoms $N/V$ is small. Corrections to the ideal gas law are often expressed in terms of a density expansion, known as the virial expansion. The most general equation of state is,

\displaystyle\frac{p}{k_{B}T}=\frac{N}{V}+B_{2}(T)\frac{N^{2}}{V^{2}}+B_{3}(T)% \frac{N^{3}}{V^{3}}+\ldots

(2.69)

where the functions $B_{j}(T)$ are known as virial coefficients.

Our goal is to compute the virial coefficients from first principles, starting from a knowledge of the underlying potential energy $U(r)$ between two neutral atoms separated by a distance $r$ . This potential has two important features:

•

An attractive $1/r^{6}$ force. This arises from fluctuating dipoles of the neutral atoms. Recall that two permanent dipole moments, $p_{1}$ and $p_{2}$ , have a potential energy which scales as $p_{1}p_{2}/r^{3}$ . Neutral atoms don’t have permanent dipoles, but they can acquire a temporary dipole due to quantum fluctuations. Suppose that the first atom has an instantaneous dipole $p_{1}$ . This will induce an electric field which is proportional to $E\sim p_{1}/r^{3}$ which, in turn, will induce a dipole of the second atom $p_{2}\sim E\sim p_{1}/r^{3}$ . The resulting potential energy between the atoms scales as $p_{1}p_{2}/r^{3}\sim 1/r^{6}$ . This is sometimes called the van der Waals interaction.
•

A rapidly rising repulsive interaction at short distances, arising from the Pauli exclusion principle that prevents two atoms from occupying the same space. For our purposes, the exact form of this repulsion is not so relevant: just as long as it’s big. (The Pauli exclusion principle is a quantum effect. If the exact form of the potential is important then we really need to be dealing with quantum mechanics all along. We will do this in the next section).

One very common potential that is often used to model the force between atoms is the Lennard-Jones potential,

\displaystyle U(r)\sim\left(\frac{r_{0}}{r}\right)^{12}-\left(\frac{r_{0}}{r}% \right)^{6}

(2.70)

The exponent $12$ is chosen only for convenience: it simplifies certain calculations because $12=2\times 6$ .

An even simpler form of the potential incorporates a hard core repulsion, in which

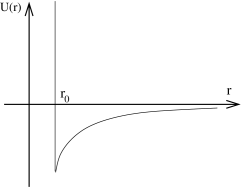
the particles are simply forbidden from closer than a fixed distance by imposing an infinite potential,

\displaystyle U(r)=\left\{\begin{array}[]{lr}\infty&r<r_{0}\\ -U_{0}\left(\frac{r_{0}}{r}\right)^{6}&r\geq r_{0}\end{array}\right.

(2.71)

The hard-core potential with van der Waals attraction is sketched to the right. We will see shortly that the virial coefficients are determined by increasingly difficult integrals involving the potential $U(r)$ . For this reason, it’s best to work with a potential that’s as simple as possible. When we come to do some actual calculations we will use the form (2.71).

2.5.1 The Mayer f Function and the Second Virial Coefficient

We’re going to change notation and call the positions of the particles $\vec{r}$ instead of $\vec{q}$ . (The latter notation was useful to stress the connection to quantum mechanics at the beginning of this Section, but we’ve now left that behind!). The Hamiltonian of the gas is

\displaystyle H=\sum_{i=1}^{N}\frac{p_{i}^{2}}{2m}+\sum_{i>j}U(r_{ij})

where $r_{ij}=|\vec{r}_{i}-\vec{r}_{j}|$ is the separation between particles. The restriction $i>j$ on the final sum ensures that we sum over each pair of particles exactly once. The partition function is then

$\displaystyle Z(N,V,T)$	$\displaystyle=$	$\displaystyle\frac{1}{N!}\frac{1}{(2\pi\hbar)^{3N}}\int\prod_{i=1}^{N}d^{3}p_{% i}d^{3}r_{i}\ e^{-\beta H}$
	$\displaystyle=$	$\displaystyle\frac{1}{N!}\frac{1}{(2\pi\hbar)^{3N}}\,\left[\int\prod_{i}d^{3}p% _{i}\ e^{-\beta\sum_{j}p_{j}^{2}/2m}\right]\times\left[\int\prod_{i}d^{3}r_{i}% \ e^{-\beta\sum_{j<k}U(r_{jk})}\right]$
	$\displaystyle=$	$\displaystyle\frac{1}{N!\lambda^{3N}}\int\prod_{i}d^{3}r_{i}\ e^{-\beta\sum_{j% <k}U(r_{jk})}$

where $\lambda$ is the thermal wavelength that we met in (2.54). We still need to do the integral over positions. And that looks hard! The interactions mean that the integrals don’t factor in any obvious way. What to do? One obvious way thing to try is to Taylor expand (which is closely related to the so-called cumulant expansion in this context)

\displaystyle e^{-\beta\sum_{j<k}U(r_{jk})}=1-\beta\sum_{j<k}U(r_{jk})+\frac{% \beta^{2}}{2}\sum_{j<k,l<m}U(r_{jk})U(r_{lm})+\ldots

Unfortunately, this isn’t so useful. We want each term to be smaller than the preceding one. But as $r_{ij}\rightarrow 0$ , the potential $U(r_{ij})\rightarrow\infty$ , which doesn’t look promising for an expansion parameter.

Instead of proceeding with the naive Taylor expansion, we will instead choose to work with the following quantity, usually called the Mayer f function,

\displaystyle f(r)=e^{-\beta U(r)}-1

(2.72)

This is a nicer expansion parameter. When the particles are far separated at $r\rightarrow\infty$ , $f(r)\rightarrow 0$ . However, as the particles come close and $r\rightarrow 0$ , the Mayer function approaches $f(r)\rightarrow-1$ . We’ll proceed by trying to construct a suitable expansion in terms of $f$ . We define

\displaystyle f_{ij}=f(r_{ij})

Then we can write the partition function as

	$\displaystyle Z(N,V,T)$	$\displaystyle=$	$\displaystyle\frac{1}{N!\lambda^{3N}}\int\prod_{i}d^{3}r_{i}\,\prod_{j>k}(1+f_% {jk})$		(2.73)
		$\displaystyle=$	$\displaystyle\frac{1}{N!\lambda^{3N}}\int\prod_{i}d^{3}r_{i}\left(1+\sum_{j>k}% f_{jk}+\sum_{j>k,l>m}f_{jk}f_{lm}+\ldots\right)$		(2.73)

The first term simply gives a factor of the volume $V$ for each integral, so we get $V^{N}$ . The second term has a sum, each element of which is the same. They all look like

\displaystyle\int\prod_{i=1}^{N}d^{3}r_{i}\ f_{12}=V^{N-2}\int d^{3}r_{1}d^{3}% r_{2}\ f(r_{12})=V^{N-1}\int d^{3}r\ f(r)

where, in the last equality, we’ve simply changed integration variables from $\vec{r}_{1}$ and $\vec{r}_{2}$ to the centre of mass $\vec{R}={\textstyle\frac{1}{2}}(\vec{r}_{1}+\vec{r}_{2})$ and the separation $\vec{r}=\vec{r}_{1}-\vec{r}_{2}$ . (You might worry that the limits of integration change in the integral over $\vec{r}$ , but the integral over $f(r)$ only picks up contributions from atomic size distances and this is only actually a problem close to the boundaries of the system where it is negligible). There is a term like this for each pair of particles – that is ${\textstyle\frac{1}{2}}N(N-1)$ such terms. For $N\sim 10^{23}$ , we can just call this a round ${\textstyle\frac{1}{2}}N^{2}$ . Then, ignoring terms quadratic in $f$ and higher, the partition function is approximately

	$\displaystyle Z(N,V,T)$	$\displaystyle=$	$\displaystyle\frac{V^{N}}{N!\lambda^{3N}}\left(1+\frac{N^{2}}{2V}\int d^{3}r\ % f(r)+\ldots\right)$
		$\displaystyle=$	$\displaystyle Z_{\rm ideal}\left(1+\frac{N}{2V}\int d^{3}r\ f(r)+\ldots\right)% ^{N}$

where we’ve used our previous result that $Z_{\rm ideal}=V^{N}/N!\lambda^{3N}$ . We’ve also engaged in something of a sleight of hand in this last line, promoting one power of $N$ from in front of the integral to an overall exponent. Massaging the expression in this way ensures that the free energy is proportional to the number of particles as one would expect:

\displaystyle F=-k_{B}T\log Z=F_{\rm ideal}-Nk_{B}T\log\left(1+\frac{N}{2V}% \int d^{3}r\ f(r)\right)

(2.74)

However, if you’re uncomfortable with this little trick, it’s not hard to convince yourself that the result (2.75) below for the equation of state doesn’t depend on it. We will also look at the expansion more closely in the following section and see how all the higher order terms work out.

From the expression (2.74) for the free energy, it is clear that we are indeed performing an expansion in density of the gas since the correction term is proportional to $N/V$ . This form of the free energy will give us the second virial coefficient $B_{2}(T)$ .

We can be somewhat more precise about what it means to be at low density. The exact form of the integral $\int d^{3}rf(r)$ depends on the potential, but for both the Lennard-Jones potential (2.70) and the hard-core repulsion (2.71), the integral is approximately $\int d^{3}rf(r)\sim r_{0}^{3}$ , where $r_{0}$ is roughly the minimum of the potential. (We’ll compute the integral exactly below for the hard-core potential). For the expansion to be valid, we want each term with an extra power of $f$ to be smaller than the preceding one. (This statement is actually only approximately true. We’ll be more precise below when we develop the cluster expansion). That means that the second term in the argument of the $\log$ should be smaller than 1. In other words,

\displaystyle\frac{N}{V}\ll\frac{1}{r_{0}^{3}}

The left-hand side is the density of the gas. The right-hand side is atomic density. Or, equivalently, the density of a substance in which the atoms are packed closely together. But we have a name for such substances – we call them liquids! Our expansion is valid for densities of the gas that are much lower than that of the liquid state.

2.5.2 van der Waals Equation of State

We can use the free energy (2.74) to compute the pressure of the gas. Expanding the logarithm as $\log(1+x)\approx x$ we get

\displaystyle p=-\frac{\partial{F}}{\partial{V}}=\frac{Nk_{B}T}{V}\left(1-% \frac{N}{2V}\int d^{3}rf(r)+\ldots\right)

As expected, the pressure deviates from that of an ideal gas. We can characterize this by writing

\displaystyle\frac{pV}{Nk_{B}T}=1-\frac{N}{2V}\int d^{3}r\ f(r)

(2.75)

To understand what this is telling us, we need to compute $\int d^{3}rf(r)$ . Firstly let’s look at two trivial examples:

Repulsion: Suppose that $U(r)>0$ for all separations $r$ with $U(r=\infty)=0$ . Then $f=e^{-\beta U}-1<0$ and the pressure increases, as we’d expect for a repulsive interaction.

Attraction: If $U(r)<0$ , we have $f>0$ and the pressure decreases, as we’d expect for an attractive interaction.

What about a more realistic interaction that is attractive at long distances and repulsive at short? We will compute the equation of state of a gas using the hard-core potential with van der Waals attraction (2.71). The integral of the Mayer $f$ function is

\displaystyle\int d^{3}r\ f(r)=\int_{0}^{r_{0}}d^{3}r(-1)+\int_{r_{0}}^{\infty% }d^{3}r\ (e^{+\beta U_{0}(r_{0}/r)^{6}}-1)

(2.76)

We’ll approximate the second integral in the high temperature limit, $\beta U_{0}\ll 1$ , where $e^{+\beta U_{0}(r_{0}/r)^{6}}\approx 1+\beta U_{0}(r_{0}/r)^{6}$ . Then

	$\displaystyle\int d^{3}r\ f(r)$	$\displaystyle=$	$\displaystyle-4\pi\int_{0}^{r_{0}}dr\,r^{2}+\frac{4\pi U_{0}}{k_{B}T}\int_{r_{% 0}}^{\infty}dr\ \frac{r_{0}^{6}}{r^{4}}$
		$\displaystyle=$	$\displaystyle\frac{4\pi r_{0}^{3}}{3}\left(\frac{U_{0}}{k_{B}T}-1\right)$

Inserting this into (2.75) gives us an expression for the equation of state,

\displaystyle\frac{pV}{Nk_{B}T}=1-\frac{N}{V}\left(\frac{a}{k_{B}T}-b\right)

We recognise this expansion as capturing the second virial coefficient in (2.69) as promised. The constants $a$ and $b$ are defined by

\displaystyle a=\frac{2\pi r_{0}^{3}U_{0}}{3}\ \ \ ,\ \ \ b=\frac{2\pi r_{0}^{% 3}}{3}

It is actually slightly more useful to write this in the form $k_{B}T=\ldots$ . We can multiply through by $k_{B}T$ then, rearranging we have

\displaystyle k_{B}T=\frac{V}{N}\left(p+\frac{N^{2}}{V^{2}}a\right)\left(1+% \frac{N}{V}b\right)^{-1}

Since we’re working in an expansion in density, $N/V$ , we’re at liberty to Taylor expand the last bracket, keeping only the first two terms. We get

\displaystyle k_{B}T=\left(p+\frac{N^{2}}{V^{2}}a\right)\left(\frac{V}{N}-b\right)

(2.78)

This is the famous van der Waals equation of state for a gas. We stress again the limitations of our analysis: it is valid only at low densities and (because of our approximation when performing the integral (2.76)) at high temperatures.

We will return to the van der Waals equation in Section 5 where we’ll explore many of its interesting features. For now, we can get a feeling for the physics behind this equation of state by rewriting it in yet another way,

\displaystyle p=\frac{Nk_{B}T}{V-bN}-a\frac{N^{2}}{V^{2}}

(2.79)

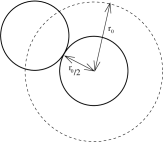
The constant $a$ contains a factor of $U_{0}$ and so capures the effect of the attractive interaction at large distances. We see that its role is to reduce the pressure of the gas. The reduction in pressure is proportional to the density squared because this is, in turn, proportional to the number of pairs of particles which feel the attractive force. In contrast, $b$ only contains $r_{0}$ and arises due to the hard-core repulsion in the potential. Its effect is the reduce the effective volume of the gas because of the space taken up by the particles.

It is worth pointing out where some quizzical factors of two come from in $b=2\pi r_{0}^{3}/3$ . Recall that $r_{0}$ is the minimum distance that two atoms can approach. If we think of the each atom as a hard sphere, then they have radius $r_{0}/2$ and volume $4\pi(r_{0}/2)^{3}/3$ . Which isn’t equal to $b$ . However, as illustrated in the figure, the excluded volume around each atom is actually $\Omega=4\pi r_{0}^{3}/3=2b$ . So why don’t we have $\Omega$ sitting in the denominator of the van der Waals equation rather than $b=\Omega/2$ ? Think about adding the atoms one at a time. The first guy can move in volume $V$ ; the second in volume $V-\Omega$ ; the third in volume $V-2\Omega$ and so on. For $\Omega\ll V$ , the total configuration space available to the atoms is

\displaystyle\frac{1}{N!}\prod_{m=1}^{N}\left(V-m\Omega\right)\approx\frac{V^{% N}}{N!}\left(1-\frac{N^{2}}{2}\frac{\Omega}{V}+\ldots\right)\approx\frac{1}{N!% }\left(V-\frac{N\Omega}{2}\right)^{N}

And there’s that tricky factor of $1/2$ .

Above we computed the equation of state for the dipole van der Waals interaction with hard core potential. But our expression (2.75) can seemingly be used to compute the equation of state for any potential between atoms. However, there are limitations. Looking back to the integral (2.5.2), we see that a long-range force of the form $1/r^{n}$ will only give rise to a convergent integral for $n\geq 4$ . This means that the techniques described above do not work for long-range potentials with fall-off $1/r^{3}$ or slower. This includes the important case of $1/r$ Coulomb interactions.

2.5.3 The Cluster Expansion

Above we computed the leading order correction to the ideal gas law. In terms of the virial expansion (2.69) this corresponds to the second virial coefficient $B_{2}$ . We will now develop the full expansion and explain how to compute the higher virial coefficients.

Let’s go back to equation (2.73) where we first expressed the partition function in terms of $f$ ,

	$\displaystyle Z(N,V,T)$	$\displaystyle=$	$\displaystyle\frac{1}{N!\lambda^{3N}}\int\prod_{i}d^{3}r_{i}\,\prod_{j>k}(1+f_% {jk})$		(2.80)
		$\displaystyle=$	$\displaystyle\frac{1}{N!\lambda^{3N}}\int\prod_{i}d^{3}r_{i}\left(1+\sum_{j>k}% f_{jk}+\sum_{j>k,l>m}f_{jk}f_{lm}+\ldots\right)$		(2.80)

Above we effectively related the second virial coefficient to the term linear in $f$ : this is the essence of the equation of state (2.75). One might think that terms quadratic in $f$ give rise to the third virial coefficient and so on. But, as we’ll now see, the expansion is somewhat more subtle than that.

The expansion in (2.80) includes terms of the form $f_{ij}f_{kl}f_{mn}\ldots$ where the indices denote pairs of atoms, $(i,j)$ and $(k,l)$ and so on. These pairs may have atoms in common or they may all be different. However, the same pair never appears twice in a given term as you may check by going back to the first line in (2.80). We’ll introduce a diagrammatic method to keep track of all the terms in the sum. To each term of the form $f_{ij}f_{kl}f_{mn}\ldots$ we associate a picture using the following rules

•

Draw $N$ atoms. (This gets tedious for $N\sim 10^{23}$ but, as we’ll soon see, we will actually only need pictures with small subset of atoms).
•

Draw a line between each pair of atoms that appear as indices. So for $f_{ij}f_{kl}f_{mn}\ldots$ , we draw a line between atom $i$ and atom $j$ ; a line between atom $k$ and atom $l$ ; and so on.

For example, if we have just $N=4$ , we have the following pictures for different terms in the expansion,

\displaystyle f_{12}=\raisebox{-10.75pt}{\epsfbox{cluster1.eps}}\ \ \ \ \ \ \ % \ f_{12}f_{34}=\raisebox{-10.75pt}{\epsfbox{cluster2.eps}}\ \ \ \ \ \ \ \ \ f_% {12}f_{23}=\raisebox{-10.75pt}{\epsfbox{cluster3.eps}}\ \ \ \ \ \ \ \ \ f_{21}% f_{23}f_{31}=\raisebox{-10.75pt}{\epsfbox{cluster4.eps}}

We call these diagrams graphs. Each possible graph appears exactly once in the partition function (2.80). In other words, the partition function is a sum over all graphs. We still have to do the integrals over all positions $\vec{r}_{i}$ . We will denote the integral over graph $G$ to be $W[G]$ . Then the partition function is

\displaystyle Z(N,V,T)=\frac{1}{N!\lambda^{3N}}\sum_{G}W[G]

Nearly all the graphs that we can draw will have disconnected components. For example, those graphs that correspond to just a single $f_{ij}$ will have two atoms connected and the remaining $N-2$ sitting alone. Those graphs that correspond to $f_{ij}f_{kl}$ fall into two categories: either they consist of two pairs of atoms (like the second example above) or, if $(i,j)$ shares an atom with $(k,l)$ , there are three linked atoms (like the third example above). Importantly, the integral over positions $\vec{r}_{i}$ then factorises into a product of integrals over the positions of atoms in disconnected components. This is illustrated by an example with $N=5$ atoms,

\displaystyle W\left[\raisebox{-9.03pt}{\epsfbox{cluster5.eps}}\ \right]=\left% (\int d^{3}r_{1}d^{3}r_{2}d^{3}r_{3}f_{12}f_{23}f_{31}\right)\left(\int d^{3}r% _{4}d^{3}r_{5}f_{45}\right)

We call the disconnected components of the graph clusters. If a cluster has $l$ atoms, we will call it an $l$ -cluster. The $N=5$ example above has a single 3-cluster and a single 2-cluster. In general, a graph $G$ will split into $m_{l}$ $l$ -clusters. Clearly, we must have

\displaystyle\sum_{l=1}^{N}m_{l}l=N

(2.81)

Of course, for a graph with only a few lines and lots of atoms, nearly all the atoms will be in lonely 1-clusters.

We can now make good on the promise above that we won’t have to draw all $N\sim 10^{23}$ atoms. The key idea is that we can focus on clusters of $l$ -atoms. We will organise the expansion in such a way that the $(l+1)$ -clusters are less important than the $l$ -clusters. To see how this works, let’s focus on $3$ -clusters for now. There are four different ways that we can have a $3$ -cluster,

Each of these 3-clusters will appear in a graph with any other combination of clusters among the remaining $N-3$ atoms. But since clusters factorise in the partition function, we know that $Z$ must include a factor

\displaystyle U_{3}\equiv\int d^{3}r_{1}d^{3}r_{2}d^{3}r_{3}\left(\ \raisebox{% -10.32pt}{\epsfbox{cluster7.eps}}\ \right)

$U_{3}$ contains terms of order $f^{2}$ and $f^{3}$ . It turns out that this is the correct way to arrange the expansion: not in terms of the number of lines in the diagram, which is equal to the power of $f$ , but instead in terms of the number of atoms that they connect. The partition function will similarly contain factors associated to all other $l$ -clusters. We define the corresponding integrals as

\displaystyle U_{l}\equiv\int\prod_{i=1}^{l}d^{3}r_{i}\sum_{G\in\{\mbox{$l$-% cluster}\}}G

(2.82)

Notice that $U_{1}$ is simply the integral over space, namely $U_{1}=V$ . The full partition function must be a product of $U_{l}$ ’s. The tricky part is to get all the combinatoric factors right to make sure that you count each graph exactly once. The sum over graphs $G$ that appears in the partition function turns out to be

\displaystyle\sum_{G}W[G]=N!\sum_{\{m_{l}\}}\prod_{l}\frac{U_{l}^{m_{l}}}{(l!)% ^{m_{l}}m_{l}!}

(2.83)

The product $N!/\prod_{l}\,m_{l}!(l!)^{m_{l}}$ counts the number of ways to split the particles into $m_{l}$ $l$ -clusters, while ignoring the different ways to internally connect each cluster. This is the right thing to do since the different internal connections are taken into account in the integral $U_{l}$ .

Combinatoric arguments are not always transparent. Let’s do a couple of checks to make sure that this is indeed the right answer. Firstly, consider $N=4$ atoms split into two 2-clusters (i.e $m_{2}=2$ ). There are three such diagrams, $f_{12}f_{34}=\raisebox{-6.02pt}{\epsfbox{cluster8.eps}}$ , $f_{13}f_{24}=\raisebox{-6.02pt}{\epsfbox{cluster9.eps}}$ , and $f_{14}f_{23}=\raisebox{-6.02pt}{\epsfbox{cluster10.eps}}$ . Each of these gives the same answer when integrated, namely $U_{2}^{2}$ so the final result should be $3U_{2}^{2}$ . We can check this against the relevant terms in (2.83) which are $4!U_{2}^{2}/2!^{2}2!=3U_{2}^{2}$ as expected.

Another check: $N=5$ atoms with $m_{2}=m_{3}=1$ . All diagrams come in the combinations

\displaystyle U_{3}U_{2}=\int\prod_{i=1}^{5}d^{3}r_{i}\left(\ \raisebox{-10.32% pt}{\epsfbox{cluster11.eps}}\ \right)

together with graphs that are related by permutations. The permutations are fully determined by the choice of the two atoms that sit in the pair: there are 10 such choices. The answer should therefore be $10U_{3}U_{2}$ . Comparing to (2.83), we have $5!U_{3}U_{2}/3!2!=10U_{3}U_{2}$ as required.

Hopefully you are now convinced that (2.83) counts the graphs correctly. The end result for the partition function is therefore

\displaystyle Z(N,V,T)=\frac{1}{\lambda^{3N}}\sum_{\{m_{l}\}}\prod_{l}\frac{U_% {l}^{m_{l}}}{(l!)^{m_{l}}m_{l}!}

The problem with computing this sum is that we still have to work out the different ways that we can split $N$ atoms into different clusters. In other words, we still have to obey the constraint (2.81). Life would be very much easier if we didn’t have to worry about this. Then we could just sum over any $m_{l}$ , regardless. Thankfully, this is exactly what we can do if we work in the grand canonical ensemble where $N$ is not fixed! The grand canonical ensemble is

\displaystyle{\cal Z}(\mu,V,T)=\sum_{N}e^{\beta\mu N}Z(N,V,T)

We define the fugacity as $z=e^{\beta\mu}$ . Then we can write

\displaystyle{\cal Z}(\mu,V,T)=\sum_{N}z^{n}Z(N,V,T)=\sum_{m_{l}=0}^{\infty}% \prod_{l=1}^{\infty}\left(\frac{z}{\lambda^{3}}\right)^{m_{l}l}\frac{1}{m_{l}!% }\left(\frac{U_{l}}{l!}\right)^{m_{l}}=\ \prod_{l=1}^{\infty}\exp\left(\frac{U% _{l}z^{l}}{\lambda^{3l}l!}\right)

One usually defines

\displaystyle b_{l}=\frac{\lambda^{3}}{V}\frac{U_{l}}{l!\lambda^{3l}}

(2.84)

Notice in particular that $U_{1}=V$ so this definition gives $b_{1}=1$ . Then we can write the grand partition function as

\displaystyle{\cal Z}(\mu,V,T)=\prod_{l=1}^{\infty}\exp\left(\frac{V}{\lambda^% {3}}b_{l}z^{l}\right)=\exp\left(\frac{V}{\lambda^{3}}\sum_{l=1}^{\infty}b_{l}z% ^{l}\right)

(2.85)

Something rather cute happened here. The sum over all diagrams got rewritten as the exponential over the sum of all connected diagrams, meaning all clusters. This is a general lesson which also carries over to quantum field theory where the diagrams in question are Feynman diagrams.

Back to the main plot of our story, we can now compute the pressure

\displaystyle\frac{pV}{k_{B}T}=\log{\cal Z}=\frac{V}{\lambda^{3}}\sum_{l=1}^{% \infty}b_{l}z^{l}

and the number of particles

\displaystyle\frac{N}{V}=\frac{z}{V}\frac{\partial}{\partial z}\log{\cal Z}=% \frac{1}{\lambda^{3}}\sum_{l=1}^{\infty}lb_{l}z^{l}

(2.86)

Dividing the two gives us the equation of state,

\displaystyle\frac{pV}{Nk_{B}T}=\frac{\sum_{l}b_{l}z^{l}}{\sum_{l}lb_{l}z^{l}}

(2.87)

The only downside is that the equation of state is expressed in terms of $z$ . To massage it into the form of the virial expansion (2.69), we need to invert (2.86) to get $z$ in terms of the particle density $N/V$ . Equating (2.87) with (2.69) (and defining $B_{1}=1$ ), we have

$\displaystyle\sum_{l=1}^{\infty}b_{l}z^{l}$	$\displaystyle=$	$\displaystyle\sum_{l=1}^{\infty}B_{l}\left(\frac{N}{V}\right)^{l-1}\,\sum_{m=1% }^{\infty}mb_{m}z^{m}$
	$\displaystyle=$	$\displaystyle\sum_{l=1}^{\infty}\frac{B_{l}}{\lambda^{3(l-1)}}\left(\sum_{n=1}% ^{\infty}nb_{n}z^{n}\right)^{l-1}\sum_{m=1}^{\infty}mb_{m}z^{m}$
	$\displaystyle=$	$\displaystyle\left[1+\frac{B_{2}}{\lambda^{3}}(z+2b_{2}z^{2}+3b_{3}z^{3}+% \ldots)+\frac{B_{3}}{\lambda^{6}}(z+2b_{2}z^{2}+3b_{3}z^{3}+\ldots)^{2}+\ldots\right]$
		$\displaystyle\ \ \ \ \times\left[z+2b_{2}z^{2}+3b_{3}z^{3}+\ldots\right]$

where we’ve used both $B_{1}=1$ and $b_{1}=1$ . Expanding out the left- and right-hand sides to order $z^{3}$ gives

\displaystyle z+b_{2}z^{2}+b_{3}z^{3}+\ldots=z+\left(\frac{B_{2}}{\lambda^{3}}% +2b_{2}\right)z^{2}+\left(3b_{3}+\frac{4b_{2}B_{2}}{\lambda^{3}}+\frac{B_{3}}{% \lambda^{3}}\right)z^{3}+\ldots

Comparing terms, and recollecting the definitions of $b_{l}$ (2.84) in terms of $U_{l}$ (2.82) in terms of graphs, we find the second virial coefficient is given by

\displaystyle B_{2}=-\lambda^{3}b_{2}=-\frac{U_{2}}{2V}=-\frac{1}{2V}\int d^{3% }r_{1}d^{3}r_{2}f(\vec{r}_{1}-\vec{r}_{2})=-\frac{1}{2}\int d^{3}rf(r)

which reproduces the result (2.75) that we found earlier using slightly simpler methods. We now also have an expression for the third coefficient,

\displaystyle B_{3}=\lambda^{6}(4b_{2}^{2}-2b_{3})

although admittedly we still have a nasty integral to do before we have a concrete result. More importantly, the cluster expansion gives us the technology to perform a systematic perturbation expansion to any order we wish.

2.6 Screening and the Debye-Hückel Model of a Plasma

There are many other applications of the classical statistical methods that we saw in this chapter. Here we use them to derive the important phenomenon of screening. The problem we will consider, which sometimes goes by the name of a “one-component plasma”, is the following: a gas of electrons, each with charge $-q$ , moves in a fixed background of uniform positive charge density $+q\rho$ . The charge density is such that the overall system is neutral which means that $\rho$ is also the average charge density of the electrons. This is the Debye-Hückel model.

In the absence of the background charge density, the interaction between electons is given by the Coulomb potential

\displaystyle U(r)=\frac{q^{2}}{r}

where we’re using units in which $4\pi\epsilon_{0}=1$ . How does the fixed background charge affect the potential between electrons? The clever trick of the Debye-Hückel model is to use statistical methods to figure out the answer to this question. Consider placing one electron at the origin. Let’s try to work out the electrostatic potential $\phi(\vec{r})$ due to this electron. It is not obvious how to do this because $\phi$ will also depend on the positions of all the other electrons. In general we can write,

\displaystyle\nabla^{2}\phi(\vec{r})=-4\pi\left(-q\delta(\vec{r})+q\rho-q\rho g% (\vec{r})\right)

(2.88)

where the first term on the right-hand side is due to the electron at the origin; the second term is due to the background positive charge density; and the third term is due to the other electrons whose average charge density close to the first electron is $\rho g(\vec{r})$ . The trouble is that we don’t know the function $g$ . If we were sitting at zero temperature, the electrons would try to move apart as much as possible. But at non-zero temperatures, their thermal energy will allow them to approach each other. This is the clue that we need. The energy cost for an electron to approach the origin is, of course, $E(\vec{r})=-q\phi(\vec{r})$ . We will therefore assume that the charge density near the origin is given by the Boltzmann factor,

\displaystyle g(\vec{r})\approx e^{\beta q\phi(\vec{r})}

For high temperatures, $\beta q\phi\ll 1$ , we can write $e^{\beta q\phi}\approx 1+\beta q\phi$ and the Poisson equation (2.88) becomes

\displaystyle\left(\nabla^{2}+\frac{1}{\lambda_{D}^{2}}\right)\phi(\vec{r})=4% \pi q\delta(\vec{r})

where $\lambda_{D}^{2}=1/4\pi\beta\rho q^{2}$ . This equation has the solution,

\displaystyle\phi(\vec{r})=-\frac{qe^{-r/\lambda_{D}}}{r}

(2.89)

which immediately translates into an effective potential energy between electrons,

\displaystyle U_{\rm eff}(r)=\frac{q^{2}e^{-r/\lambda_{D}}}{r}

We now see that the effect of the plasma is to introduce the exponential factor in the numerator, causing the potential to decay very quickly at distances $r>\lambda_{D}$ . This effect is called screening and $\lambda_{D}$ is known as the Debye screening length. The derivation of (2.89) is self-consistent if we have a large number of electrons within a distance $\lambda_{D}$ of the origin so that we can happily talk about average charge density. This means that we need $\rho\lambda_{D}^{3}\gg 1$ .