5 Phase Transitions
A phase transition is an abrupt, discontinuous change in the properties of a system. We’ve already seen one example of a phase transition in our discussion of Bose-Einstein condensation. In that case, we had to look fairly closely to see the discontinuity: it was lurking in the derivative of the heat capacity. In other phase transitions — many of them already familiar — the discontinuity is more manifest. Examples include steam condensing to water and water freezing to ice.
In this section we’ll explore a couple of phase transitions in some detail and extract some lessons that are common to all transitions.
5.1 Liquid-Gas Transition
Recall that we derived the van der Waals equation of state for a gas (2.79) in Section 2.5. We can write the van der Waals equation as
| (5.180) |
where is the volume per particle. In the literature, you will also see this equation written in terms of the particle density .
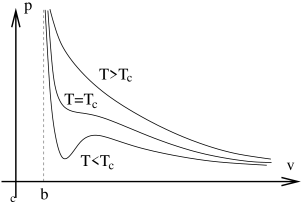
On the right we fix at different values and sketch the graph of vs. determined by the van der Waals equation. These curves are isotherms — line of constant temperature. As we can see from the diagram, the isotherms take three different shapes depending on the value of . The top curve shows the isotherm for large values of . Here we can effectively ignore the term. (Recall that cannot take values smaller than , reflecting the fact that atoms cannot approach to arbitrarily closely). The result is a monotonically decreasing function, essentially the same as we would get for an ideal gas. In contrast, when is low enough, the second term in (5.180) can compete with the first term. Roughly speaking, this happens when is in the allowed region . For these low value of the temperature, the isotherm has a wiggle.
At some intermediate temperature, the wiggle must flatten out so that the bottom curve looks like the top one. This happens when the maximum and minimum meet to form an inflection point. Mathematically, we are looking for a solution to . it is simple to check that these two equations only have a solution at the critical temperature given by
| (5.181) |
Let’s look in more detail at the curve. For a range of pressures, the system can have three different choices of volume. A typical, albeit somewhat exagerated, example of this curve is shown in the figure below. What’s going on? How should we interpret the fact that the system can seemingly live at three different densities ?
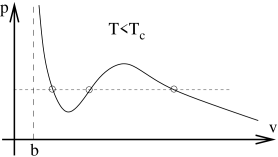
First look at the middle solution. This has some fairly weird properties. We can see from the graph that the gradient is positive: . This means that if we apply a force to the container to squeeze the gas, the pressure decreases. The gas doesn’t push back; it just relents. But if we expand the gas, the pressure increases and the gas pushes harder. Both of these properties are telling us that the gas in that state is unstable. If we were able to create such a state, it wouldn’t hand around for long because any tiny perturbation would lead to a rapid, explosive change in its density. If we want to find states which we are likely to observe in Nature then we should look at the other two solutions.
The solution to the left on the graph has slightly bigger than . But, recall from our discussion of Section 2.5 that is the closest that the atoms can get. If we have , then the atoms are very densely packed. Moreover, we can also see from the graph that is very large for this solution which means that the state is very difficult to compress: we need to add a great deal of pressure to change the volume only slightly. We have a name for this state: it is a liquid.
You may recall that our original derivation of the van der Waals equation was valid only for densities much lower than the liquid state. This means that we don’t really trust (5.180) on this solution. Nonetheless, it is interesting that the equation predicts the existence of liquids and our plan is to gratefully accept this gift and push ahead to explore what the van der Waals tells us about the liquid-gas transition. We will see that it captures many of the qualitative features of the phase transition.
The last of the three solutions is the one on the right in the figure. This solution has and small . It is the gas state. Our goal is to understand what happens in between the liquid and gas state. We know that the naive, middle, solution given to us by the van der Waals equation is unstable. What replaces it?
5.1.1 Phase Equilibrium
Throughout our derivation of the van der Waals equation in Section 2.5, we assumed that the system was at a fixed density. But the presence of two solutions — the liquid and gas state — allows us to consider more general configurations: part of the system could be a liquid and part could be a gas.
How do we figure out if this indeed happens? Just because both liquid and gas states can exist, doesn’t mean that they can cohabit. It might be that one is preferred over the other. We already saw some conditions that must be satisfied in order for two systems to sit in equilibrium back in Section 1. Mechanical and thermal equilibrium are guaranteed if two systems have the same pressure and temperature respectively. But both of these are already guaranteed by construction for our two liquid and gas solutions: the two solutions sit on the same isotherm and at the same value of . We’re left with only one further requirement that we must satisfy which arises because the two systems can exchange particles. This is the requirement of chemical equilibrium,
| (5.182) |
Because of the relationship (4.175) between the chemical potential and the Gibbs free energy, this is often expressed as
| (5.183) |
where is the Gibbs free energy per particle.
Notice that all the equilibrium conditions involve only intensive quantities: , and . This means that if we have a situation where liquid and gas are in equilibrium, then we can have any number of atoms in the liquid state and any number in the gas state. But how can we make sure that chemical equilibrium (5.182) is satisfied?
Maxwell Construction
We want to solve . We will think of the chemical potential as a function of and : . Importantly, we won’t assume that is single valued since that would be assuming the result we’re trying to prove! Instead we will show that if we fix , the condition (5.182) can only be solved for a very particular value of pressure . To see this, start in the liquid state at some fixed value of and and travel along the isotherm. The infinitesimal change in the chemical potential is
However, we can get an expression for by recalling that arguments involving extensive and intensive variables tell us that the chemical potential is proportional to the Gibbs free energy: (4.175). Looking back at the variation of the Gibbs free energy (4.174) then tells us that
| (5.184) |

Integrating along the isotherm then tells us the chemical potential of any point on the curve,
When we get to gas state at the same pressure that we started from, the condition for equilibrium is . Which means that the integral has to vanish. Graphically this is very simple to describe: the two shaded areas in the graph must have equal area. This condition, known as the Maxwell construction, tells us the pressure at which gas and liquid can co-exist.
I should confess that there’s something slightly dodgy about the Maxwell construction. We already argued that the part of the isotherm with suffers an instability and is unphysical. But we needed to trek along that part of the curve to derive our result. There are more rigorous arguments that give the same answer.
For each isotherm, we can determine the pressure at which the liquid and gas states are in equilibrium. The gives us the co-existence curve, shown by the dotted line in Figure 37. Inside this region, liquid and gas can both exist at the same temperature and pressure. But there is nothing that tells us how much gas there should be and how much liquid: atoms can happily move from the liquid state to the gas state. This means that while the density of gas and liquid is fixed, the average density of the system is not. It can vary between the gas density and the liquid density simply by changing the amount of liquid. The upshot of this argument is that inside the co-existence curves, the isotherms simply become flat lines, reflecting the fact that the density can take any value. This is shown in graph on the right of Figure 37.

To illustrate the physics of this situation, suppose that we sit at some fixed density and cool the system down from a high temperature to at a point inside the co-existence curve so that we’re now sitting on one of the flat lines. Here, the system is neither entirely liquid, nor entirely gas. Instead it will split into gas, with density , and liquid, with density so that the average density remains . The system undergoes phase separation. The minimum energy configuration will typically be a single phase of liquid and one of gas because the interface between the two costs energy. (We will derive an expression for this energy in Section 5.5). The end result is shown on the right. In the presence of gravity, the higher density liquid will indeed sink to the bottom.
Meta-Stable States
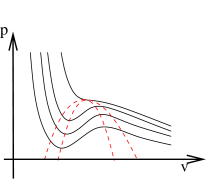
We’ve understood what replaces the unstable region of the van der Waals phase diagram. But we seem to have removed more states than anticipated: parts of the Van der Waals isotherm that had are contained in the co-existence region and replaced by the flat pressure lines. This is the region of the - phase diagram that is contained between the two dotted lines in the figure to the right. The outer dotted line is the co-existence curve. The inner dotted curve is constructed to pass through the stationary points of the van der Waals isotherms. It is called the spinodal curve.
The van der Waals states which lie between the spinodal curve and the co-existence curve are good states. But they are meta-stable. One can show that their Gibbs free energy is higher than that of the liquid-gas equilibrium at the same and . However, if we compress the gas very slowly we can coax the system into this state. It is known as a supercooled vapour. It is delicate. Any small disturbance will cause some amount of the gas to condense into the liquid. Similarly, expanding a liquid beyond the co-existence curve results in an meta-stable, superheated liquid.
5.1.2 The Clausius-Clapeyron Equation
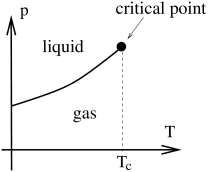
We can also choose to plot the liquid-gas phase diagram on the plane. Here the co-existence region is squeezed into a line: if we’re sitting in the gas phase and increase the pressure just a little bit at at fixed then we jump immediately to the liquid phase. This appears as a discontinuity in the volume. Such discontinuities are the sign of a phase transition. The end result is sketched in the figure to the right; the thick solid line denotes the presence of a phase transition.
Either side of the line, all particles are either in the gas or liquid phase. We know from (5.183) that the Gibbs free energies (per particle) of these two states are equal,
So is continuous as we move across the line of phase transitions. Suppose that we sit on the line itself and move along it. How does change? We can easily compute this from (4.174),
where, just as an , the entropy density is . Equating this with the free energy in the gaseous phase gives
This can be rearranged to gives us a nice expression for the slope of the line of phase transitions in the plane. It is
We usually define the specific latent heat
This is the energy released per particle as we pass through the phase transition. We see that the slope of the line in the plane is determined by the ratio of latent heat released in the phase transition and the discontinuity in volume. The result is known as the Clausius-Clapeyron equation,
| (5.185) |
There is a classification of phase transitions, due originally to Ehrenfest. When the derivative of a thermodynamic potential (either or usually) is discontinuous, we say we have an order phase transition. In practice, we nearly always deal with first, second and (very rarely) third order transitions. The liquid-gas transition releases latent heat, which means that is discontinuous. Alternatively, we can say that is discontinuous. Either way, it is a first order phase transition. The Clausius-Clapeyron equation (5.185) applies to any first order transition.
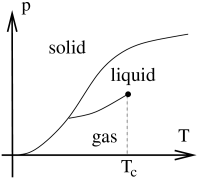
As we approach , the discontinuity diminishes and . At the critical point we have a second order phase transition. Above the critical point, there is no sharp distinction between the gas phase and liquid phase.
For most simple materials, the phase diagram above is part of a larger phase diagram which includes solids at smaller temperatures or higher pressures. A generic version of such a phase diagram is shown to the right. The van der Waals equation is missing the physics of solidification and includes only the liquid-gas line.
An Approximate Solution to the Clausius-Clapeyron Equation
We can solve the Clausius-Clapeyron solution if we make the following assumptions:
-
•
The latent heat is constant.
-
•
, so . For water, this is an error of less than
-
•
Although we derived the phase transition using the van der Waals equation, now we’ve got equation (5.185) we’ll pretend the gas obeys the ideal gas law .
With these assumptions, it is simple to solve (5.185). It reduces to
5.1.3 The Critical Point
Let’s now return to discuss some aspects of life at the critical point. We previously worked out the critical temperature (5.181) by looking for solutions to simultaneous equations . There’s a slightly more elegant way to find the critical point which also quickly gives us and as well. We rearrange the van der Waals equation (5.180) to get a cubic,
For , this equation has three real roots. For there is just one. Precisely at , the three roots must therefore coincide (before two move off onto the complex plane). At the critical point, this curve can be written as
Comparing the coefficients tells us the values at the critical point,
| (5.186) |
The Law of Corresponding States
We can invert the relations (5.186) to express the parameters and in terms of the critical values, which we then substitute back into the van der Waals equation. To this end, we define the reduced variables,
The advantage of working with , and is that it allows us to write the van der Waals equation (5.180) in a form that is universal to all gases, usually referred to as the law of corresponding states
Moreover, because the three variables , and at the critical point are expressed in terms of just two variables, and (5.186), we can construct a combination of them which is independent of and and therefore supposedly the same for all gases. This is the universal compressibility ratio,
| (5.187) |
Comparing to real gases, this number is a little high. Values range from around 0.28 to 0.3. We shouldn’t be too discouraged by this; after all, we knew from the beginning that the van der Waals equation is unlikely to be accurate in the liquid regime. Moreover, the fact that gases have a critical point (defined by three variables , and ) guarantees that a similar relationship would hold for any equation of state which includes just two parameters (such as and ) but would most likely fail to hold for equations of state that included more than two parameters.
Dubious as its theoretical foundation is, the law of corresponding states is the first suggestion that something remarkable happens if we describe a gas in terms of its reduced variables. More importantly, there is striking experimental evidence to back this up! Figure 42 shows the Guggenheim plot, constructed in 1945. The co-existence curve for 8 different gases in plotted in reduced variables: along the vertical axis; along the horizontal. The gases vary in complexity from the simple monatomic gas to the molecule . As you can see, the co-existence curve for all gases is essentially the same, with the chemical make-up largely forgotten. There is clearly something interesting going on. How to understand it?
Critical Exponents
We will focus attention on physics close to the critical point. It is not immediately obvious what are the right questions to ask. It turns out that the questions which have the most interesting answer are concerned with how various quantities change as we approach the critical point. There are lots of ways to ask questions of this type since there are many quantities of interest and, for each of them, we could approach the critical point from different directions. Here we’ll look at the behaviour of three quantities to get a feel for what happens.
First, we can ask what happens to the difference in (inverse) densities as we approach the critical point along the co-existence curve. For , or equivalently , the reduced van der Waals equation (5.187) has two stable solutions,
If we solve this for , we have
Notice that as we approach the critical point, and the equation above tells us that as expected. We can see exactly how we approach by expanding the right right-hand side for small . To do this quickly, it’s best to notice that the equation is symmetric in and , so close to the critical point we can write and . Substituting this into the equation above and keeping just the leading order term, we find
Or, re-arranging, as we approach along the co-existence curve,
| (5.188) |
This is the answer to our first question.
Our second variant of the question is: how does the volume change with pressure as we move along the critical isotherm. It turns out that we can answer this question without doing any work. Notice that at , there is a unique pressure for a given volume . But we know that at the critical point. So a Taylor expansion around the critical point must start with the cubic term,
| (5.189) |
This is the answer to our second question.
Our third and final variant of the question concerns the compressibility, defined as
| (5.190) |
We want to understand how changes as we approach from above. In fact, we met the compressibility before: it was the feature that first made us nervous about the van der Waals equation since is negative in the unstable region. We already know that at the critical point . So expanding for temperatures close to , we expect
This tells us that the compressibility should diverge at the critical point, scaling as
| (5.191) |
We now have three answers to three questions: (5.188), (5.189) and (5.191). Are they right?! By which I mean: do they agree with experiment? Remember that we’re not sure that we can trust the van der Waals equation at the critical point so we should be nervous. However, there is also reason for some confidence. Notice, in particular, that in order to compute (5.189) and (5.191), we didn’t actually need any details of the van der Waals equation. We simply needed to assume the existence of the critical point and an analytic Taylor expansion of various quantities in the neighbourhood. Given that the answers follow from such general grounds, one may hope that they provide the correct answers for a gas in the neighbourhood of the critical point even though we know that the approximations that went into the van der Waals equation aren’t valid there. Fortunately, that isn’t the case: physics is much more interesting than that!
The experimental results for a gas in the neighbourhood of the critical point do share one feature in common with the discussion above: they are completely independent of the atomic make-up of the gas. However, the scaling that we computed using the van der Waals equation is not fully accurate. The correct results are as follows. As we approach the critical point along the co-existence curve, the densities scale as
(Note that the exponent has nothing to do with inverse temperature. We’re just near the end of the course and running out of letters and is the canonical name for this exponent). As we approach along an isotherm,
Finally, as we approach from above, the compressibility scales as
The quantities , and are examples of critical exponents. We will see more of them shortly. The van der Waals equation provides only a crude first approximation to the critical exponents.
Fluctuations
We see that the van der Waals equation didn’t do too badly in capturing the dynamics of an interacting gas. It gets the qualitative behaviour right, but fails on precise quantitative tests. So what went wrong? We mentioned during the derivation of the van der Waals equation that we made certain approximations that are valid only at low density. So perhaps it is not surprising that it fails to get the numbers right near the critical point . But there’s actually a deeper reason that the van der Waals equation fails: fluctuations.
This is simplest to see in the grand canonical ensemble. Recall that back in Section 1 that we argued that , which allowed us to happily work in the grand canonical ensemble even when we actually had fixed particle number. In the context of the liquid-gas transition, fluctuating particle number is the same thing as fluctuating density . Let’s revisit the calculation of near the critical point. Using (1.45) and (1.48), the grand canonical partition function can be written as , so the average particle number (1.42) is
We already have an expression for the variance in the particle number in (1.43),
Dividing these two expressions, we have
But we can re-write this expression using the general relationship between partial derivatives . We then have
This final expression relates the fluctuations in the particle number to the compressibility (5.190). But the compressibility is diverging at the critical point and this means that there are large fluctuations in the density of the fluid at this point. The result is that any simple equation of state, like the van der Waals equation, which works only with the average volume, pressure and density will miss this key aspect of the physics.
Understanding how to correctly account for these fluctuations is the subject of critical phenomena. It has close links with the renormalization group and conformal field theory which also arise in particle physics and string theory. You will meet some of these ideas in next year’s Statistical Field Theory course. Here we will turn to a different phase transition which will allow us to highlight some of the key ideas.
5.2 The Ising Model
The Ising model is one of the touchstones of modern physics; a simple system that exhibits non-trivial and interesting behaviour.
The Ising model consists of sites in a -dimensional lattice. On each lattice site lives a quantum spin that can sit in one of two states: spin up or spin down. We’ll call the eigenvalue of the spin on the lattice site . If the spin is up, ; if the spin is down, .
The spins sit in a magnetic field that endows an energy advantage to those which point up,
(A comment on notation: should be properly denoted . We’re sticking with to avoid confusion with the Hamiltonian. There is also a factor of the magnetic moment which has been absorbed into the definition of ). The lattice system with energy is equivalent to the two-state system that we first met when learning the techniques of statistical mechanics back in Section 1.2.3. However, the Ising model contains an additional complication that makes the sysem much more interesting: this is an interaction between neighbouring spins. The full energy of the system is therefore,
| (5.192) |
The notation means that we sum over all “nearest neighbour” pairs in the lattice. The number of such pairs depends both on the dimension and the type of lattice. We’ll denote the number of nearest neighbours as . For example, in a lattice has ; in , a square lattice has . A square lattice in dimensions has .
If , neighbouring spins prefer to be aligned ( or ). In the context of magnetism, such a system is called a ferromagnet. If , the spins want to anti-align (). This is an anti-ferromagnet. In the following, we’ll choose although for the level of discussion needed for this course, the differences are minor.
We work in the canonical ensemble and introduce the partition function
| (5.193) |
While the effect of both and is to make it energetically preferable for the spins to align, the effect of temperature will be to randomize the spins, with entropy winnning out over energy. Our interest is in the average spin, or average magnetization
| (5.194) |
The Ising Model as a Lattice Gas
Before we develop techniques to compute the partition function (5.193), it’s worth pointing out that we can drape slightly different words around the mathematics of the Ising model. It need not be interpreted as a system of spins; it can also be thought of as a lattice description of a gas.
To see this, consider the same -dimensional lattice as before, but now with particles hopping between lattice sites. These particles have hard cores, so no more than one can sit on a single lattice site. We introduce the variable to specify whether a given lattice site, labelled by , is empty () or filled (. We can also introduce an attractive force between atoms by offering them an energetic reward if they sit on neighbouring sites. The Hamiltonian of such a lattice gas is given by
where is the chemical potential which determines the overall particle number. But this Hamiltonian is trivially the same as the Ising model (5.192) if we make the identification
The chemical potenial in the lattice gas plays the role of magnetic field in the spin system while the magnetization of the system (5.194) measures the average density of particles away from half-filling.
5.2.1 Mean Field Theory
For general lattices, in arbitrary dimension , the sum (5.193) cannot be performed. An exact solution exists in and, when , in . (The solution is originally due to Onsager and is famously complicated! Simpler solutions using more modern techniques have since been discovered).
Here we’ll develop an approximate method to evaluate known as mean field theory. We write the interactions between neighbouring spins in term of their deviation from the average spin ,
The mean field approximation means that we assume that the fluctuations of spins away from the average are small which allows us to neglect the first term above. Notice that this isn’t the statement that the variance of an individual spin is small; that can never be true because takes values or so and the variance is always large. Instead, the mean field approximation is a statement about fluctuations between spins on neighbouring sites, so the first term above can be neglected when summing over . We can then write the energy (5.192) as
| (5.195) | |||||
where the factor of in the first term is simply the number of nearest neighbour pairs . The factor or is there because is a sum over pairs rather than a sum of individual sites. (If you’re worried about this formula, you should check it for a simple square lattice in and dimensions). A similar factor in the second term cancelled the factor of due to .
We see that the mean field approximation has removed the interactions. The Ising model reduces to the two state system that we saw way back in Section 1. The result of the interactions is that a given spin feels the average effect of its neighbour’s spins through a contribution to the effective magnetic field,
|
|
Once we’ve taken into account this extra contribution to , each spin acts independently and it is easy to write the partition function. It is
| (5.196) | |||||
However, we’re not quite done. Our result for the partition function depends on which depends on which we don’t yet know. However, we can use our expression for to self-consistently determine the magnetization (5.194). We find,
| (5.197) |
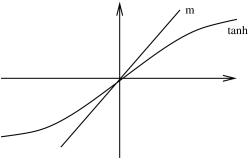
We can now solve this equation to find the magnetization for various values of and : . It is simple to see the nature of the solutions using graphical methods.
B=0
Let’s first consider the situation with vanishing magnetic field, . The figures above show the graph linear in compared with the function. Since , the slope of the graph near the origin is given by . This then determines the nature of the solution.
-
•
The first graph depicts the situation for . The only solution is . This means that at high temperatures , there is no average magnetization of the system. The entropy associated to the random temperature flucutations wins over the energetically preferred ordered state in which the spins align.
-
•
The second graph depicts the situation for . Now there are three solutions: and . It will turn out that the middle solution, , is unstable. (This solution is entirely analogous to the unstable solution of the van der Waals equation. We will see this below when we compute the free energy). For the other two possible solutions, , the magnetization is non-zero. Here we see the effects of the interactions begin to win over temperature. Notice that in the limit of vanishing temperature, , . This means that all the spins are pointing in the same direction (either up or down) as expected.
-
•
The critical temperature separating these two cases is
(5.198)
The results described above are perhaps rather surprising. Based on the intuition that things in physics always happen smoothly, one might have thought that the magnetization would drop slowly to zero as . But that doesn’t happen. Instead the magnetization turns off abruptly at some finite value of the temperature , with no magnetization at all for higher temperatures. This is the characteristic behaviour of a phase transition.
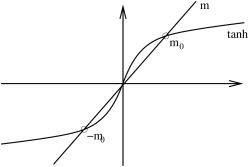
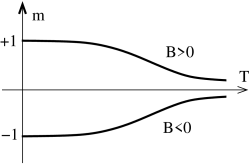
For , we can solve the consistency equation (5.197) in a similar fashion. There are a couple of key differences to the case. Firstly, there is now no phase transition at fixed as we vary temperature . Instead, for very large temperatures , the magnetization goes smoothly to zero as
At low temperatures, the magnetization again asymptotes to the state which minimizes the energy. Except this time, there is no ambiguity as to whether the system chooses or . This is entirely determined by the sign of the magnetic field .
In fact the low temperature behaviour requires slightly more explanation. For small values of and , there are again three solutions to (5.197). This follows simply from continuity: there are three solutions for and shown in Figure 44 and these must survive in some neighbourhood of . One of these solutions is again unstable. However, of the remaining two only one is now stable: that with . The other is meta-stable. We will see why this is the case shortly when we come to discuss the free energy.
|
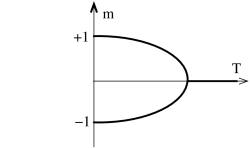
|
The net result of our discussion is depicted in the figures above. When there is a phase transition at . For , the system can sit in one of two magnetized states with . In contrast, for , there is no phase transition as we vary temperature and the system has at all times a preferred magnetization whose sign is determined by that of . Notice however, we do have a phase transition if we fix temperature at and vary from negative to positive. Then the magnetization jumps discontinuously from a negative value to a positive value. Since the magnetization is a first derivative of the free energy (5.194), this is a first order phase transition. In contrast, moving along the temperature axis at results in a second order phase transition at .
5.2.2 Critical Exponents
It is interesting to compare the phase transition of the Ising model with that of the liquid-gas phase transition. The two are sketched in the Figure 47 above. In both cases, we have a first order phase transition and a quantity jumps discontinuously at . In the case of the liquid-gas, it is the density that jumps as we vary pressure; in the case of the Ising model it is the magnetization that jumps as we vary the magnetic field. Moreover, in both cases the discontinuity disappears as we approach .
We can calculate critical exponents for the Ising model. To compare with our discussion for the liquid-gas critical point, we will compute three quantities. First, consider the magnetization at . We can ask how this magnetization decreases as we tend towards the critical point. Just below , is small and we can Taylor expand (5.197) to get
The magnetization therefore scales as
| (5.199) |
This is to be compared with the analogous result (5.188) from the van der Waals equation. We see that the values of the exponents are the same in both cases. Notice that the derivative becomes infinite as we approach the critical point. In fact, we had already anticipated this when we drew the plot of the magnetization in Figure 45.
Secondly, we can sit at and ask how the magnetization changes as we approach . We can read this off from (5.197). At we have and the consistency condition becomes . Expanding for small gives
So we find that the magnetization scales as
| (5.200) |
Notice that this power of is again familiar from the liquid-gas transition (5.189) where the van der Waals equation gave .
Finally, we can look at the magnetic susceptibility , defined as
This is analogous to the compressibility of the gas. We will ask how changes as we approach from above at . We differentiate (5.197) with respect to to get
We now evaluate this at . Since we want to approach from above, we can also set in the above expression. Evaluating this at gives us the scaling
| (5.201) |
Once again, we see that same critical exponent that the van der Waals equation gave us for the gas (5.191).
5.2.3 Validity of Mean Field Theory
The phase diagram and critical exponents above were all derived using the mean field approximation. But this was an unjustified approximation. Just as for the van der Waals equation, we can ask the all-important question: are our results right?
There is actually a version of the Ising model for which the mean field theory is exact: it is the dimensional lattice. This is unphysical (even for a string theorist). Roughly speaking, mean field theory works for large because each spin has a large number of neighbours and so indeed sees something close to the average spin.
But what about dimensions of interest? Mean field theory gets things most dramatically wrong in . In that case, no phase transition occurs. We will derive this result below where we briefly describe the exact solution to the Ising model. There is a general lesson here: in low dimensions, both thermal and quantum fluctuations are more important and invariably stop systems forming ordered phases.
In higher dimensions, , the crude features of the phase diagram, including the existence of a phase transition, given by mean field theory are essentially correct. In fact, the very existence of a phase transition is already worthy of comment. The defining feature of a phase transition is behaviour that jumps discontinuously as we vary or . Mathematically, the functions must be non-analytic. Yet all properties of the theory can be extracted from the partition function which is a sum of smooth, analytic functions (5.193). How can we get a phase transition? The loophole is that is only necessarily analytic if the sum is finite. But there is no such guarantee when the number of lattice sites . We reach a similar conclusion to that of Bose-Einstein condensation: phase transitions only strictly happen in the thermodynamic limit. There are no phase transitions in finite systems.
What about the critical exponents that we computed in (5.199), (5.200) and (5.201)? It turns out that these are correct for the Ising model defined in . (We will briefly sketch why this is true at the end of this Chapter). But for and , the critical exponents predicted by mean field theory are only first approximations to the true answers.
For , the exact solution (which goes quite substantially past this course) gives the critical exponents to be,
The biggest surprise is in dimensions. Here the critical exponents are not known exactly. However, there has been a great deal of numerical work to determine them. They are given by
But these are exactly the same critical exponents that are seen in the liquid-gas phase transition. That’s remarkable! We saw above that the mean field approach to the Ising model gave the same critical exponents as the van der Waals equation. But they are both wrong. And they are both wrong in the same, complicated, way! Why on earth would a system of spins on a lattice have anything to do with the phase transition between a liquid and gas? It is as if all memory of the microscopic physics — the type of particles, the nature of the interactions — has been lost at the critical point. And that’s exactly what happens.
What we’re seeing here is evidence for universality. There is a single theory which describes the physics at the critical point of the liquid gas transition, the 3d Ising model and many other systems. This is a theoretical physicist’s dream! We spend a great deal of time trying to throw away the messy details of a system to focus on the elegant essentials. But, at a critical point, Nature does this for us! Although critical points in two dimensions are well understood, there is still much that we don’t know about critical points in three dimensions. This, however, is a story that will have to wait for another day.
5.3 Some Exact Results for the Ising Model
This subsection is something of a diversion from our main interest. In later subsections, we will develop the idea of mean field theory. But first we pause to describe some exact results for the Ising model using techniques that do not rely on the mean field approximation. Many of the results that we derive have broader implications for systems beyond the Ising model.
As we mentioned above, there is an exact solution for the Ising model in dimension and, when , in dimensions. Here we will describe the solution but not the full solution. We will, however, derive a number of results for the Ising model which, while falling short of the full solution, nonetheless provide important insights into the physics.
5.3.1 The Ising Model in Dimensions
We start with the Ising chain, the Ising model on a one dimensional line. Here we will see that the mean field approximation fails miserably, giving qualitatively incorrect results: the exact results shows that there are no phase transitions in the Ising chain.
The energy of the system (5.192) can be trivially rewritten as
We will impose periodic boundary conditions, so the spins live on a circular lattice with . The partition function is then
| (5.202) |
The crucial observation that allows us to solve the problem is that this partition function can be written as a product of matrices. We adopt notation from quantum mechanics and define the matrix,
| (5.203) |
The row of the matrix is specified by the value of and the column by . is known as the transfer matrix and, in more conventional notation, is given by
The sums over the spins and product over lattice sites in (5.202) simply tell us to multiply the matrices defined in (5.203) and the partition function becomes
| (5.204) |
where the trace arises because we have imposed periodic boundary conditions. To complete the story, we need only compute the eigenvalues of to determine the partition function. A quick calculation shows that the two eigenvalues of are
| (5.205) |
where, clearly, . The partition function is then
| (5.206) |
where, in the last step, we’ve used the simple fact that if is the largest eigenvalue then for very large .
The partition function contains many quantities of interest. In particular, we can use it to compute the magnetisation as a function of temperature when . This, recall, is the quantity which is predicted to undergo a phase transition in the mean field approximation, going abruptly to zero at some critical temperature. In the Ising model, the magnetisation is given by
We see that the true physics for is very different than that suggested by the mean field approximation. When , there is no magnetisation! While the term in the energy encourages the spins to align, this is completely overwhelmed by thermal fluctuations for any value of the temperature.
There is a general lesson in this calculation: thermal fluctuations always win in one dimensional systems. They never exhibit ordered phases and, for this reason, never exhibit phase transitions. The mean field approximation is bad in one dimension.
5.3.2 2d Ising Model: Low Temperatures and Peierls Droplets
Let’s now turn to the Ising model in dimensions. We’ll work on a square lattice and set . Rather than trying to solve the model exactly, we’ll have more modest goals. We will compute the partition function in two different limits: high temperature and low temperature. We start here with the low temperature expansion.
The partition function is given by the sum over all states, weighted by . At low temperatures, this is always dominated by the lowest lying states. For the Ising model, we have
The low temperature limit is , where the partition function can be approximated by the sum over the first few lowest energy states. All we need to do is list these states.
The ground states are easy. There are two of them: spins all up or spins all down. For example, the ground state with spins all up looks like
Each of these ground states has energy .
The first excited states arise by flipping a single spin. Each spin has nearest neighbours – denoted by red lines in the example below – each of which leads to an energy cost of . The energy of each first excited state is therefore .
There are, of course, different spins that we we can flip and, correspondingly, the first energy level has a degeneracy of .
To proceed, we introduce a diagrammatic method to list the different states. We draw only the “broken” bonds which connect two spins with opposite orientation and, as in the diagram above, denote these by red lines. We further draw the flipped spins as red dots, the unflipped spins as blue dots. The energy of the state is determined simply by the number of red lines in the diagram. Pictorially, we write the first excited state as
The next lowest state has six broken bonds. It takes the form
where the extra factor of 2 in the degeneracy comes from the two possible orientations (vertical and horizontal) of the graph.
Things are more interesting for the states which sit at the third excited level. These have 8 broken bonds. The simplest configuration consists of two, disconnected, flipped spins
| (5.207) |
The factor of in the degeneracy comes from placing the first graph; the factor of arises because the flipped spin in the second graph can sit anywhere apart from on the five vertices used in the first graph. Finally, the factor of arises from the interchange of the two graphs.
There are also three further graphs with the same energy . These are
and
where the degeneracy comes from the two orientations (vertical and horizontal). And, finally,
where the degeneracy comes from the four orientations (rotating the graph by ).
Adding all the graphs above together gives us an expansion of the partition function in power of . This is
| (5.208) |
where the overall factor of 2 originates from the two ground states of the system. We’ll make use of the specific coefficients in this expansion in Section 5.3.4. Before we focus on the physics hiding in the low temperature expansion, it’s worth making a quick comment that something quite nice happens if we take the log of the partition function,
The thing to notice is that the term in the partition function (5.208) has cancelled out and is proportional to , which is to be expected since the free energy of the system is extensive. Looking back, we see that the term was associated to the disconnected diagrams in (5.207). There is actually a general lesson hiding here: the partition function can be written as the exponential of the sum of connected diagrams. We saw exactly the same issue arise in the cluster expansion in (2.85).
Peierls Droplets
Continuing the low temperature expansion provides a heuristic, but physically intuitive, explanation for why phase transitions happen in dimensions but not in . As we flip more and more spins, the low energy states become droplets, consisting of a region of space in which all the spins are flipped, surrounded by a larger sea in which the spins have their original alignment. The energy cost of such a droplet is roughly
where is the perimeter of the droplet. Notice that the energy does not scale as the area of the droplet since all spins inside are aligned with their neighbours. It is only those on the edge which are misaligned and this is the reason for the perimeter scaling. To understand how these droplets contribute to the partition function, we also need to know their degeneracy. We will now argue that the degeneracy of droplets scales as
for some value of . To see this, consider firstly the problem of a random walk on a 2d square lattice. At each step, we can move in one of four directions. So the number of paths of length is
Of course, the perimeter of a droplet is more constrained that a random walk. Firstly, the perimeter can’t go back on itself, so it really only has three directions that it can move in at each step. Secondly, the perimeter must return to its starting point after steps. And, finally, the perimeter cannot self-intersect. One can show that the number of paths that obey these conditions is
where . Since the degeneracy scales as , the entropy of the droplets is proportional to .
The fact that both energy and entropy scale with means that there is an interesting competition between them. At temperatures where the droplets are important, the partition function is schematically of the form
For large (i.e. low temperature) the partition function converges. However, as the temperature increases, one reaches the critical temperature
| (5.209) |
where the partition function no longer converges. At this point, the entropy wins over the energy cost and it is favourable to populate the system with droplets of arbitrary sizes. This is the how one sees the phase transition in the partition function. For temperature above , the low-temperature expansion breaks down and the ordered magnetic phase is destroyed.
We can also use the droplet argument to see why phase transitions don’t occur in dimension. On a line, the boundary of any droplet always consists of just two points. This means that the energy cost to forming a droplet is always , regardless of the size of the droplet. But, since the droplet can exist anywhere along the line, its degeneracy is . The net result is that the free energy associated to creating a droplet scales as
and, as , the free energy is negative for any . This means that the system will prefer to create droplets of arbitrary length, randomizing the spins. This is the intuitive reason why there is no magnetic ordered phase in the Ising model.
5.3.3 2d Ising Model: High Temperatures
We now turn to the 2d Ising model in the opposite limit of high temperature. Here we expect the partition function to be dominated by the completely random, disordered configurations of maximum entropy. Our goal is to find a way to expand the partition function in .
We again work with zero magnetic field, and write the partition function as
There is a useful way to rewrite which relies on the fact that the product only takes . It doesn’t take long to check the following identity:
Using this, the partition function becomes
| (5.210) | |||||
where the number of nearest neighbours is for the 2d square lattice.
With the partition function in this form, there is a natural expansion which suggests itself. At high temperatures which, of course, means that . But the partition function is now naturally a product of powers of . This is somewhat analogous to the cluster expansion for the interacting gas that we met in Section 2.5.3. As in the cluster expansion, we will represent the expansion graphically.
We need no graphics for the leading order term. It has no factors of and is simply
That’s simple.
Let’s now turn to the leading correction. Expanding the partition function (5.210), each power of is associated to a nearest neighbour pair . We’ll represent this by drawing a line on the lattice:
But there’s a problem: each factor of in (5.210) also comes with a sum over all spins and . And these are and which means that they simply sum to zero,
How can we avoid this? The only way is to make sure that we’re summing over an even number of spins on each site, since then we get factors of and no cancellations. Graphically, this means that every site must have an even number of lines attached to it. The first correction is then of the form
There are such terms since the upper left corner of the square can be on any one of the lattice sites. (Assuming periodic boundary conditions for the lattice). So including the leading term and first correction, we have
We can go further. The next terms arise from graphs of length 6 and the only possibilities are rectangles, oriented as either landscape or portrait. Each of them can sit on one of sites, giving a contribution
Things get more interesting when we look at graphs of length 8. We have four different types of graphs. Firstly, there are the trivial, disconnected pair of squares
Here the first factor of is the possible positions of the first square; the factor of arises because the possible location of the upper corner of the second square can’t be on any of the vertices of the first, but nor can it be on the square one to the left of the upper corner of the first since that would give a graph that looks like which has three lines coming off the middle site and therefore vanishes when we sum over spins. Finally, the factor of comes because the two squares are identical.
The other graphs of length 8 are a large square, a rectangle and a corner. The large square gives a contribution
There are two orientations for the rectangle. Including these gives a factor of 2,
Finally, the corner graph has four orientations, giving
Adding all contributions together gives us the first few terms in high temperature expansion of the partition function
| (5.211) | |||||
There’s some magic hiding in this expansion which we’ll turn to in Section 5.3.4. First, let’s just see how the high energy expansion plays out in the dimensional Ising model.
The Ising Chain Revisited

Let’s do the high temperature expansion for the Ising chain with periodic boundary conditions and . We have the same partition function (5.210) and the same issue that only graphs with an even number of lines attached to each vertex contribute. But, for the Ising chain, there is only one such term: it is the closed loop. This means that the partition function is
In the limit , at high temperatures and even the contribution from the closed loop vanishes. We’re left with
This agrees with our exact result for the Ising chain given in (5.206), which can be seen by setting in (5.205) so that .
5.3.4 Kramers-Wannier Duality
In the previous sections we computed the partition function perturbatively in two extreme regimes of low temperature and high temperature. The physics in the two cases is, of course, very different. At low temperatures, the partition function is dominated by the lowest energy states; at high temperatures it is dominated by maximally disordered states. Yet comparing the partition functions at low temperature (5.208) and high temperature (5.211) reveals an extraordinary fact: the expansions are the same! More concretely, the two series agree if we exchange
| (5.212) |
Of course, we’ve only checked the agreement to the first few orders in perturbation theory. Below we shall prove that this miracle continues to all orders in perturbation theory. The symmetry of the partition function under the interchange (5.212) is known as Kramers-Wannier duality. Before we prove this duality, we will first just assume that it is true and extract some consequences.
We can express the statement of the duality more clearly. The Ising model at temperature is related to the same model at temperature , defined as
| (5.213) |
This way of writing things hides the symmetry of the transformation. A little algebra shows that this is equivalent to
Notice that this is a hot/cold duality. When is large, is small. Kramers-Wannier duality is the statement that, when , the partition functions of the Ising model at two temperatures are related by
| (5.214) | |||||
This means that if you know the thermodynamics of the Ising model at one temperature, then you also know the thermodynamics at the other temperature. Notice however, that it does not say that all the physics of the two models is equivalent. In particular, when one system is in the ordered phase, the other typically lies in the disordered phase.
One immediate consequence of the duality is that we can use it to compute the exact critical temperature . This is the temperature at which the partition function in singular in the limit. (We’ll discuss a more refined criterion in Section 5.4.3). If we further assume that there is just a single phase transition as we vary the temperature, then it must happen at the special self-dual point . This is
The exact solution of Onsager confirms that this is indeed the transition temperature. It’s also worth noting that it’s fully consistent with the more heuristic Peierls droplet argument (5.209) since .
Proving the Duality
So far our evidence for the duality (5.214) lies in the agreement of the first few terms in the low and high temperature expansions (5.208) and (5.211). Of course, we could keep computing further and further terms and checking that they agree, but it would be nicer to simply prove the equality between the partition functions. We shall do so here.
The key idea that we need can actually be found by staring hard at the various graphs that arise in the two expansions. Eventually, you will realise that they are the same, albeit drawn differently. For example, consider the two “corner” diagrams
The two graphs are dual. The red lines in the first graph intersect the black lines in the second as can be seen by placing them on top of each other:
The same pattern occurs more generally: the graphs appearing in the low temperature expansion are in one-to-one correspondence with the dual graphs of the high temperature expansion. Here we will show how this occurs and how one can map the partition functions onto each other.
Let’s start by writing the partition function in the form (5.210) that we met in the high temperature expansion and presenting it in a slightly different way,
where we have introduced the rather strange variable associated to each nearest neighbour pair that takes values and , together with the functions.
The variables in the original Ising model were spins on the lattice sites. The observation that the graphs which appear in the two expansions are dual suggests that it might be profitable to focus attention on the links between lattice sites. Clearly, we have one link for every nearest neighbour pair. If we label these links by , we can trivially rewrite the partition function as
Notice that the strange label has now become a variable that lives on the links rather than the original lattice sites .
At this stage, we do the sum over the spins . We’ve already seen that if a given spin, say , appears in a term an odd number of times, then that term will vanish when we sum over the spin. Alternatively, if the spin appears an even number of times, then the sum will give 2. We’ll say that a given link is turned on in configurations with and turned off when . In this language, a term in the sum over spin contributes only if an even number of links attached to site are turned on. The partition function then becomes
| (5.215) |
Now we have something interesting. Rather than summing over spins on lattice sites, we’re now summing over the new variables living on links. This looks like the partition function of a totally different physical system, where the degrees of freedom live on the links of the original lattice. But there’s a catch – that big “Constrained” label on the sum. This is there to remind us that we don’t sum over all configurations; only those for which an even number of links are turned on for every lattice site. And that’s annoying. It’s telling us that the aren’t really independent variables. There are some constraints that must be imposed.
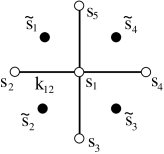
Fortunately, for the 2d square lattice, there is a simple way to solve the constraint. We introduce yet more variables, which, like the original spin variables, take values . However, the do not live on the original lattice sites. Instead, they live on the vertices of the dual lattice. For the 2d square lattice, the dual vertices are drawn in the figure. The original lattice sites are in white; the dual lattice sites in black.
The link variables are related to the two nearest spin variables as follows:
Notice that we’ve replaced four variables taking values with four variables taking values . Each set of variables gives possibilities. However, the map is not one-to-one. It is not possible to construct for all values of using the parameterization in terms of . To see this, we need only look at
In other words, the number of links that are turned on must be even. But that’s exactly what we want! Writing the in terms of the auxiliary spins automatically solves the constraint that is imposed on the sum in (5.215). Moreover, it is simple to check that for every configuration obeying the constraint, there are two configurations of . This means that we can replace the constrained sum over with an unconstrained sum over . The only price we pay is an additional factor of 1/2.
Finally, we’d like to find a simple expression for and in terms of . That’s easy enough. We can write
Substituting this into our newly re-written partition function gives
But this final form of the partition function in terms of the dual spins has exactly the same functional form as the original partition function in terms of the spins . More precisely, we can write
where
as advertised previously in (5.213). This completes the proof of Kramers-Wannier duality in the 2d Ising model on a square lattice.
The concept of duality of this kind is a major feature in much of modern theoretical physics. The key idea is that when the temperature gets large there may be a different set of variables in which a theory can be written where it appears to live at low temperature. The same idea often holds in quantum theories, where duality maps strong coupling problems to weak coupling problems.
The duality in the Ising model is special for two reasons: firstly, the new variables are governed by the same Hamiltonian as the original variables . We say that the Ising model is self-dual. In general, this need not be the case — the high temperature limit of one system could look like the low-temperature limit of a very different system. Secondly, the duality in the Ising model can be proven explicitly. For most systems, we have no such luck. Nonetheless, the idea that there may be dual variables in other, more difficult theories, is compelling. Commonly studied examples include the exchange particles and vortices in two dimensions, and electrons and magnetic monopoles in three dimensions.
5.4 Landau Theory
We saw in Sections 5.1 and 5.2 that the van der Waals equation and mean field Ising model gave the same (sometimes wrong!) answers for the critical exponents. This suggests that there should be a unified way to look at phase transitions. Such a method was developed by Landau. It is worth stressing that, as we saw above, the Landau approach to phase transitions often only gives qualitatively correct results. However, its advantage is that it is extremely straightforward and easy. (Certainly much easier than the more elaborate methods needed to compute critical exponents more accurately).
The Landau theory of phase transitions is based around the free energy. We will illustrate the theory using the Ising model and then explain how to extend it to different systems. The free energy of the Ising model in the mean field approximation is readily attainable from the partition function (5.196),
| (5.216) |
So far in this course, we’ve considered only systems in equilibrium. The free energy, like all other thermodynamic potentials, has only been defined on equilibrium states. Yet the equation above can be thought of as an expression for as a function of . Of course, we could substitute in the equilibrium value of given by solving (5.197), but it seems a shame to throw out when it is such a nice function. Surely we can put it to some use!
The key step in Landau theory is to treat the function seriously. This means that we are extending our viewpoint away from equilibrium states to a whole class of states which have a constant average value of . If you want some words to drape around this, you could imagine some external magical power that holds fixed. The free energy is then telling us the equilibrium properties in the presence of this magical power. Perhaps more convincing is what we do with the free energy in the absence of any magical constraint. We saw in Section 4 that equilibrium is guaranteed if we sit at the minimum of . Looking at extrema of , we have the condition
But that’s precisely the condition (5.197) that we saw previously. Isn’t that nice!
In the context of Landau theory, is called an order parameter. When it takes non-zero values, the system has some degree of order (the spins have a preferred direction in which they point) while when the spins are randomised and happily point in any direction.
For any system of interest, Landau theory starts by identifying a suitable order parameter. This should be taken to be a quantity which vanishes above the critical temperature at which the phase transition occurs, but is non-zero below the critical temperature. Sometimes it is obvious what to take as the order parameter; other times less so. For the liquid-gas transition, the relevant order parameter is the difference in densities between the two phases, . For magnetic or electric systems, the order parameter is typically some form of magnetization (as for the Ising model) or the polarization. For the Bose-Einstein condensate, superfluids and superconductors, the order parameter is more subtle and is related to off-diagonal long-range order in the one-particle density matrix1111 11 See, for example, the book “Quantum Liquids” by Anthony Leggett, although this is usually rather lazily simplified to say that the order parameter can be thought of as the macroscopic wavefunction .
Starting from the existence of a suitable order parameter, the next step in the Landau programme is to write down the free energy. But that looks tricky. The free energy for the Ising model (5.216) is a rather complicated function and clearly contains some detailed information about the physics of the spins. How do we just write down the free energy in the general case? The trick is to assume that we can expand the free energy in an analytic power series in the order parameter. For this to be true, the order parameter must be small which is guaranteed if we are close to a critical point (since for ). The nature of the phase transition is determined by the kind of terms that appear in the expansion of the free energy. Let’s look at a couple of simple examples.
5.4.1 Second Order Phase Transitions
We’ll consider a general system (Ising model; liquid-gas; BEC; whatever) and denote the order parameter as . Suppose that the expansion of the free energy takes the general form
| (5.217) |
One common reason why the free energy has this form is because the theory has a symmetry under , forbidding terms with odd powers of in the expansion. For example, this is the situation in the Ising model when . Indeed, if we expand out the free energy (5.216) for the Ising model for small using and we get the general form above with explicit expressions for , and ,
The leading term is unimportant for our story. We are interested in how the free energy changes with . The condition for equilibrium is given by
| (5.218) |
|
|
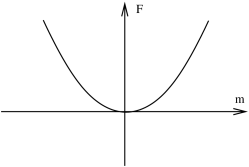
But the solutions to this equation depend on the sign of the coefficients and . Moreover, this sign can change with temperature. This is the essence of the phase transitions. In the following discussion, we will assume that for all . (If we relax this condition, we have to also consider the term in the free energy which leads to interesting results concerning so-called tri-critical points).
The two figures above show sketches of the free energy in the case where and . Comparing to the explicit free energy of the Ising model, when and when . When , we have just a single equilibrium solution to (5.218) at . This is typically the situation at high temperatures. In contrast, at , there are three solutions to (5.218). The solution clearly has higher free energy: this is now the unstable solution. The two stable solutions sit at . For example, if we choose to truncate the free energy (5.217) at quartic order, we have
If is a smooth function then the equilibrium value of changes continuously from when to at . This describes a second order phase transition occurring at , defined by .
Once we know the equilibrium value of , we can then substitute this back into the free energy in (5.217). This gives the thermodynamic free energy of the system in equilibrium that we have been studying throughout this course. For the quartic free energy, we have
| (5.219) |
Because , the equilibrium free energy is continuous at . Moreover, the entropy is also continuous at . However, if you differentiate the equilibrium free energy twice, you will get a term which is generically not vanishing at . This means that the heat capacity changes discontinuously at , as befits a second order phase transition. A word of warning: if you want to compute equilibrium quantities such as the heat capacity, it’s important that you first substitution in the equilibrium value of and work with (5.219) rather than i (5.217). If you don’t, you miss the fact that the magnetization also changes with .
We can easily compute critical exponents within the context of Landau theory. We need only make further assumptions about the behaviour of and in the vicinity of . If we assume that near , we can write
| (5.220) |
then we have
which reproduces the critical exponent (5.188) and (5.199) that we derived for the van der Waals equation and Ising model respectively.
Landau’s theory of phase transitions predicts this same critical exponent for all values of the dimension of the system. But we’ve already mentioned in previous contexts that the critical exponent is in fact only correct for . We will understand how to derive this criterion from Landau theory in the next section.
Spontaneous Symmetry Breaking
As we approach the end of the course, we’re touching upon a number of ideas that become increasingly important in subsequent developments in physics. We already briefly met the idea of universality and critical phenomena. Here I would like to point out another very important idea: spontaneous symmetry breaking.
The free energy (5.217) is invariant under the symmetry . Indeed, we said that one common reason that we can expand the free energy only in even powers of is that the underlying theory also enjoys this symmetry. But below , the system must pick one of the two ground states or . Whichever choice it makes breaks the symmetry. We say that the symmetry is spontaneously broken by the choice of ground state of the theory.
Spontaneous symmetry breaking has particularly dramatic consequences when the symmetry in question is continuous rather than discrete. For example, consider a situation where the order parameter is a complex number and the free energy is given by (5.217) with . (This is effectively what happens for BECs, superfluids and superconductors). Then we should only look at the solutions so that the ground state has . But this leaves the phase of completely undetermined. So there is now a continuous choice of ground states: we get to sit anywhere on the circle parameterised by the phase of . Any choice that the system makes spontaneously breaks the rotational symmetry which acts on the phase of . Some beautiful results due to Nambu and Goldstone show that the much of the physics of these systems can be understood simply as a consequence of this symmetry breaking. The ideas of spontaneous symmetry breaking are crucial in both condensed matter physics and particle physics. In the latter context, it is intimately tied with the Higgs mechanism.
5.4.2 First Order Phase Transitions
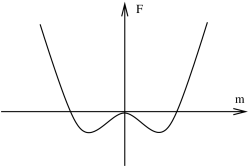
Let us now consider a situation where the expansion of the free energy also includes odd powers of the order parameter
For example, this is the kind of expansion that we get for the Ising model free energy (5.216) when , which reads
Notice that there is no longer a symmetry relating : the field has a preference for one sign over the other.
If we again assume that for all temperatures, the crude shape of the free energy graph again has two choices: there is a single minimum, or two minima and a local maximum.
Let’s start at suitably low temperatures for which the situation is depicted in Figure 52. The free energy once again has a double well, except now slightly skewed. The local maximum is still an unstable point. But this time around, the minima with the lower free energy is preferred over the other one. This is the true ground state of the system. In contrast, the point which is locally, but not globally, a minimum corresponds to a meta-stable state of the system. In order for the system to leave this state, it must first fluctuate up and over the energy barrier separating the two.
In this set-up, we can initiate a first order phase transition. This occurs when the coefficient of the odd terms, and change sign and the true ground state changes discontinuously from to . In some systems this behaviour occurs when changing temperature; in others it could occur by changing some external parameter. For example, in the Ising model the first order phase transition is induced by changing .
At very high temperature, the double well potential is lost in favour of a single minimum as depicted in the figure to the right. There is a unique ground state, albeit shifted from by the presence of the term above (which translates into the magnetic field in the Ising model). The temperature at which the meta-stable ground state of the system is lost corresponds to the spinodal point in our discussion of the liquid-gas transition.
One can play further games in Landau theory, looking at how the shape of the free energy can change as we vary temperature or other parameters. One can also use this framework to give a simple explanation of the concept of hysteresis. You can learn more about these from the links on the course webpage.
5.4.3 Lee-Yang Zeros
You may have noticed that the flavour of our discussion of phase transitions is a little different from the rest of the course. Until now, our philosophy was to derive everything from the partition function. But in this section, we dumped the partition function as soon as we could, preferring instead to work with the macroscopic variables such as the free energy. Why didn’t we just stick with the partition function and examine phase transitions directly?
The reason, of course, is that the approach using the partition function is hard! In this short section, which is somewhat tangential to our main discussion, we will describe how phase transitions manifest themselves in the partition function.
For concreteness, let’s go back to the classical interacting gas of Section 2.5, although the results we derive will be more general. We’ll work in the grand canonical ensemble, with the partition function
| (5.221) |
To regulate any potential difficulties with short distances, it is useful to assume that the particles have hard-cores so that they cannot approach to a distance less than . We model this by requiring that the potential satisfies
But this has an obvious consequence: if the particles have finite size, then there is a maximum number of particles, , that we can fit into a finite volume . (Roughly this number is ). But that, in turn, means that the canonical partition function for , and the grand partition function is therefore a finite polynomial in the fugacity , of order . But if the partition function is a finite polynomial, there can’t be any discontinuous behaviour associated with a phase transition. In particular, we can calculate
| (5.222) |
which gives us as a smooth function of . We can also calculate
| (5.223) |
which gives us as a function of . Eliminating between these two functions (as we did for both bosons and fermions in Section 3) tells us that pressure is a smooth function of density . We’re never going to get the behaviour that we derived from the Maxwell construction in which the plot of pressure vs density shown in Figure 37 exhibits a discontinous derivative.
The discussion above is just re-iterating a statement that we’ve alluded to several times already: there are no phase transitions in a finite system. To see the discontinuous behaviour, we need to take the limit . A theorem due to Lee and Yang1212 12 This theorem was first proven for the Ising model in 1952. Soon afterwards, the same Lee and Yang proposed a model of parity violation in the weak interaction for which they won the 1957 Nobel prize. gives us a handle on the analytic properties of the partition function in this limit.
The surprising insight of Lee and Yang is that if you’re interested in phase transitions, you should look at the zeros of in the complex -plane. Let’s firstly look at these when is finite. Importantly, at finite there can be no zeros on the positive real axis, . This follows follows from the defintion of given in (5.221) where it is a sum of positive quantities. Moreover, from (5.223), we can see that is a monotonically increasing function of because we necessarily have . Nonetheless, is a polynomial in of order so it certainly has zeros somewhere in the complex -plane. Since , these zeros must either sit on the real negative axis or come in complex pairs.
However, the statements above rely on the fact that is a finite polynomial. As we take the limit , the maximum number of particles that we can fit in the system diverges, , and is now defined as an infinite series. But infinite series can do things that finite ones can’t. The Lee-Yang theorem says that as long as the zeros of continue to stay away from the positive real axis as , then no phase transitions can happen. But if one or more zeros happen to touch the positive real axis, life gets more interesting.
More concretely, the Lee-Yang theorem states:
-
•
Lee-Yang Theorem: The quantity
exists for all . The result is a continuous, non-decreasing function of which is independent of the shape of the box (up to some sensible assumptions such as which ensures that the box isn’t some stupid fractal shape).
Moreover, let be a fixed, volume independent, region in the complex plane which contains part of the real, positive axis. If contains no zero of for all then is a an analytic function of for all . In particular, all derivatives of are continuous.
In other words, there can be no phase transitions in the region even in the limit. The last result means that, as long as we are safely in a region , taking derivatives of with respect to commutes with the limit . In other words, we are allowed to use (5.223) to write the particle density as
However, if we look at points where zeros appear on the positive real axis, then will generally not be analytic. If is discontinuous, then the system is said to undergo a first order phase transition. More generally, if is discontinuous for , but continuous for all , then the system undergoes an order phase transition. We won’t offer a proof of the Lee-Yang theorem. Instead illustrate the general idea with an example.
A Made-Up Example
Ideally, we would like to start with a Hamiltonian which exhibits a first order phase transition, compute the associated grand partition function and then follow its zeros as . However, as we mentioned above, that’s hard! Instead we will simply make up a partition function which has the appropriate properties. Our choice is somewhat artificial,
Here is a constant which will typically depend on temperature, although we’ll suppress this dependence in what follows. Also,
Although we just made up the form of , it does have the behaviour that one would expect of a partition function. In particular, for finite , the zeros sit at
As promised, none of the zeros sit on the positive real axis.However, as we increase , the zeros become denser and denser on the unit circle. From the Lee-Yang theorem, we expect that no phase transition will occur for but that something interesting could happen at .
Let’s look at what happens as we send . We have
We see that is continuous for all as promised. But it is only analytic for .
We can extract the physics by using (5.222) and (5.223) to eliminate the dependence on . This gives us the equation of state, with pressure as a function of . For , we have
While for , we have
They key point is that there is a jump in particle density of at . Plotting this as a function of vs , we find that we have a curve that is qualitatively identical to the pressure-volume plot of the liquid-gas phase diagram under the co-existence curve. (See, for example, figure 37). This is a first order phase transition.
5.5 Landau-Ginzburg Theory
Landau’s theory of phase transition focusses only on the average quantity, the order parameter. It ignores the fluctuations of the system, assuming that they are negligible. Here we sketch a generalisation which attempts to account for these fluctuations. It is known as Landau-Ginzburg theory.
The idea is to stick with the concept of the order parameter, . But now we allow the order parameter to vary in space so it becomes a function . Let’s restrict ourselves to the situation where there is a symmetry of the theory so we need only consider even powers in the expansion of the free energy. We add to these a gradient term whose role is to captures the fact that there is some stiffness in the system, so it costs energy to vary the order parameter from one point to another. (For the example of the Ising model, this is simply the statement that nearby spins want to be aligned). The free energy is then given by
| (5.224) |
where we have dropped the constant piece which doesn’t depend on the order parameter and hence plays no role in the story. Notice that we start with terms quadratic in the gradient: a term linear in the gradient would violate the rotational symmetry of the system.
We again require that the free energy is minimised. But now is a functional – it is a function of the function . To find the stationary points of such objects we need to use the same kind of variational methods that we use in Lagrangian mechanics. We write the variation of the free energy as
where to go from the first line to the second we have integrated by parts. (We need to remember that is a function of temperature but does not vary in space so that doesn’t act on it). The minimum of the free energy is then determined by setting which means that we have to solve the Euler-Lagrange equations for the function ,
| (5.225) |
The simplest solutions to this equation have constant, reducing us back to Landau theory. We’ll assume once again that for and for . Then the constant solutions are for and for . However, allowing for the possibility of spatial variation in the order parameter also opens up the possibility for us to search for more interesting solutions.
Domain Walls
Suppose that we have so there exist two degenerate ground states, . We could cook up a situation in which one half of space, say , lives in the ground state while the other half of space, lives in . This is exactly the situation that we already met in the liquid-gas transition and is depicted in Figure 38. It is also easy to cook up the analogous configuration in the Ising model. The two regions in which the spins point up or down are called domains. The place where these regions meet is called the domain wall.
We would like to understand the structure of the domain wall. How does the system interpolate between these two states? The transition can’t happen instantaneously because that would result in the gradient term giving an infinite contribution to the free energy. But neither can the transition linger too much because any point at which differs significantly from the value costs free energy from the and terms. There must be a happy medium between these two.
To describe the system with two domains, must vary but it need only change in one direction: . Equation (5.225) then becomes an ordinary differential equation,
This equation is easily solved. We should remember that in order to have two vacua, which means that . We then have
where is the constant ground state solution for the spin. As , the function tends towards which means that . So this solution indeed interpolates between the two domains as required. We learn that the width of the domain wall is given by . Outside of this region, the magnetisation relaxes exponentially quickly back to the ground state values.
We can also compute the cost in free energy due to the presence of the domain wall. To do this, we substitute the solution back into the expression for the free energy (5.224). The cost is not proportional to the volume of the system, but instead proportional to the area of the domain wall. This means that if the system has linear size then the free energy of the ground state scales as while the free energy required by the wall scales only as . It is simple to find the parametric dependence of this domain wall energy without doing any integrals; the energy per unit area scales as . Notice that as we approach the critical point, and , the two vacua are closer, the width of the domain wall increases and its energy decreases.
5.5.1 Correlations
One of the most important applications of Landau-Ginzburg theory is to understand the correlations between fluctuations of the system at different points in space. Suppose that we know that the system has an unusually high fluctuation away from the average at some point in space, let’s say the origin . What is the effect of this on nearby points?
There is a simple way to answer this question that requires us only to solve the differential equation (5.225). However, there is also a more complicated way to derive the same result which has the advantage of stressing the underlying physics and the role played by fluctuations. Below we’ll start by deriving the correlations in the simple manner. We’ll then see how it can also be derived using more technical machinery.
We assume that the system sits in a given ground state, say , and imagine small perturbations around this. We write the magnetisation as
| (5.226) |
If we substitute this into equation (5.225) and keep only terms linear in , we find
where we have substituted to get this result. (Recall that in the ordered phase). We now perturb the system. This can be modelled by putting a delta-function source at the origin, so that the above equation becomes
where the strength of the delta function has been chosen merely to make the equation somewhat nicer. It is straightforward to solve the asymptotic behaviour of this equation. Indeed, it is the same kind of equation that we already solved when discussing the Debye-Hückel model of screening. Neglecting constant factors, it is
| (5.227) |
This tells us how the perturbation decays as we move away from the origin. This equation has several names, reflecting the fact that it arises in many contexts. In liquids, it is usually called the Ornstein-Zernicke correlation. It also arises in particle physics as the Yukawa potential. The length scale is called the correlation length
| (5.228) |
The correlation length provides a measure of the distance it takes correlations to decay. Notice that as we approach a critical point, and the correlation length diverges. This provides yet another hint that we need more powerful tools to understand the physics at the critical point. We will now take the first baby step towards developing these tools.
5.5.2 Fluctuations
The main motivation to allow the order parameter to depend on space is to take into the account the effect of fluctuations. To see how we can do this, we first need to think a little more about the meaning of the quantity and what we can use it for.
To understand this point, it’s best if we go back to basics. We know that the true free energy of the system can be equated with the log of the partition function (1.36). We’d like to call the true free energy of the system because that’s the notation that we’ve been using throughout the course. But we’ve now called the Landau-Ginzburg functional and, while it’s closely related to the true free energy, it’s not quite the same thing as we shall shortly see. So to save some confusion, we’re going to change notation at this late stage and call the true free energy . Equation (1.36) then reads , which we write this as
We would like to understand the right way to view the functional in this framework. Here we give a heuristic and fairly handwaving argument. A fuller treatment involves the ideas of the renormalisation group.
The idea is that each microstate of the system can be associated to some specific function of the spatially varying order parameter . To illustrate this, we’ll talk in the language of the Ising model although the discussion generalises to any system. There we could consider associate a magnetisation to each lattice site by simply averaging over all the spins within some distance of that point. Clearly, this will only lead to functions that take values on lattice sites rather than in the continuum. But if the functions are suitably well behaved it should be possible to smooth them out into continuous functions which are essentially constant on distance scales smaller than the lattice spacing. In this way, we get a map from the space of microstates to the magnetisation, . But this map is not one-to-one. For example, if the averaging procedure is performed over enough sites, flipping the spin on just a single site is unlikely to have much effect on the average. In this way, many microstates map onto the same average magnetisation. Summing over just these microstates provides a first principles construction of the ,
| (5.229) |
Of course, we didn’t actually perform this procedure to get to (5.224): we simply wrote it down the most general form in the vicinity of a critical point with a bunch of unknown coefficients , and . But if we were up for a challenge, the above procedure tells us how we could go about figuring out those functions from first principles. More importantly, it also tells us what we should do with the Landau-Ginzburg free energy. Because in (5.229) we have only summed over those states that correspond to a particular value of . To compute the full partition function, we need to sum over all states. But we can do that by summing over all possible values of . In other words,
| (5.230) |
This is a tricky beast: it is a functional integral. We are integrating over all possible function , which is the same thing as performing an infinite number of integrations. (Actually, because the order parameters arose from an underlying lattice and are suitably smooth on short distance scales, the problem is somewhat mitigated).
The result (5.230) is physically very nice, albeit mathematically somewhat daunting. It means that we should view the Landau-Ginzburg free energy as a new effective Hamiltonian for a continuous variable . It arises from performing the partition function sum over much of the microscopic information, but still leaves us with a final sum, or integral, over fluctuations in an averaged quantity, namely the order parameter.
To complete the problem, we need to perform the function integral (5.230). This is hard. Here “hard” means that the majority of unsolved problems in theoretical physics can be boiled down to performing integrals of this type. Yet the fact it’s hard shouldn’t dissuade us, since there is a wealth of rich and beautiful physics hiding in the path integral, including the deep reason behind the magic of universality. We will start to explore some of these ideas in next year’s course on Statistical Field Theory.