Quick links to all software:
- Anisotropic osmosis filtering for shadow removal in images
- Preconditioned ADMM with nonlinear operator constraint
- Multi-Contrast MRI Reconstruction with Structure-Guided Total Variation
- Diffusion tensor imaging with deterministic error bounds
- Acceleration of the PDHGM on strongly convex subspaces
- Learning Filter Functions in Regularisers by Minimising Quotients
- Mathematical Imaging Methods for Mitosis Analysis in Live-Cell Phase Contrast Microscopy
Anisotropic osmosis filtering for shadow removal in images [link to software] [link to paper]
Simone Parisotto, Luca Calatroni, Marco Caliari, Carola-Bibiane Schönlieb, and Joachim Weickert

Preconditioned ADMM with nonlinear operator constraint [link to software] [download software (4 MB)]
Martin Benning, Florian Knoll, Carola-Bibiane Schönlieb and Tuomo Valkonen
 Abstract: We are presenting a modification of the well-known Alternating Direction Method of Multipliers (ADMM) algorithm with additional preconditioning that aims at solving convex optimisation problems with nonlinear operator constraints. Connections to the recently developed Nonlinear Primal-Dual Hybrid Gradient Method (NL-PDHGM) are presented, and the algorithm is demonstrated to handle the nonlinear inverse problem of parallel Magnetic Resonance Imaging (MRI).
Abstract: We are presenting a modification of the well-known Alternating Direction Method of Multipliers (ADMM) algorithm with additional preconditioning that aims at solving convex optimisation problems with nonlinear operator constraints. Connections to the recently developed Nonlinear Primal-Dual Hybrid Gradient Method (NL-PDHGM) are presented, and the algorithm is demonstrated to handle the nonlinear inverse problem of parallel Magnetic Resonance Imaging (MRI).
Reference: Martin Benning, Florian Knoll, Carola-Bibiane Schönlieb und Tuomo Valkonen, Preconditioned ADMM with nonlinear operator constraint, IFIP conference proceedings 2015.
 |
Multi-Contrast MRI Reconstruction with Structure-Guided Total Variation [download software (7 MB)]
Abstract: Magnetic resonance imaging (MRI) is a versatile imaging technique that allows different contrasts depending on the acquisition parameters. Many clinical imaging studies acquire MRI data for more than one of these contrasts---such as for instance T1 and T2 weighted images---which makes the overall scanning procedure very time consuming. As all of these images show the same underlying anatomy one can try to omit unnecessary measurements by taking the similarity into account during reconstruction. We will discuss two modifications of total variation---based on i) location and ii) direction---that take structural a priori knowledge into account and reduce to total variation in the degenerate case when no structural knowledge is available. We solve the resulting convex minimization problem with the alternating direction method of multipliers that separates the forward operator from the prior. For both priors the corresponding proximal operator can be implemented as an extension of the fast gradient projection method on the dual problem for total variation. We tested the priors on six data sets that are based on phantoms and real MRI images. In all test cases exploiting the structural information from the other contrast yields better results than separate reconstruction with total variation in terms of standard metrics like peak signal-to-noise ratio and structural similarity index. Furthermore, we found that exploiting the two dimensional directional information results in images with well defined edges, superior to those reconstructed solely using a priori information about the edge location.
|
|
|
Example Result:
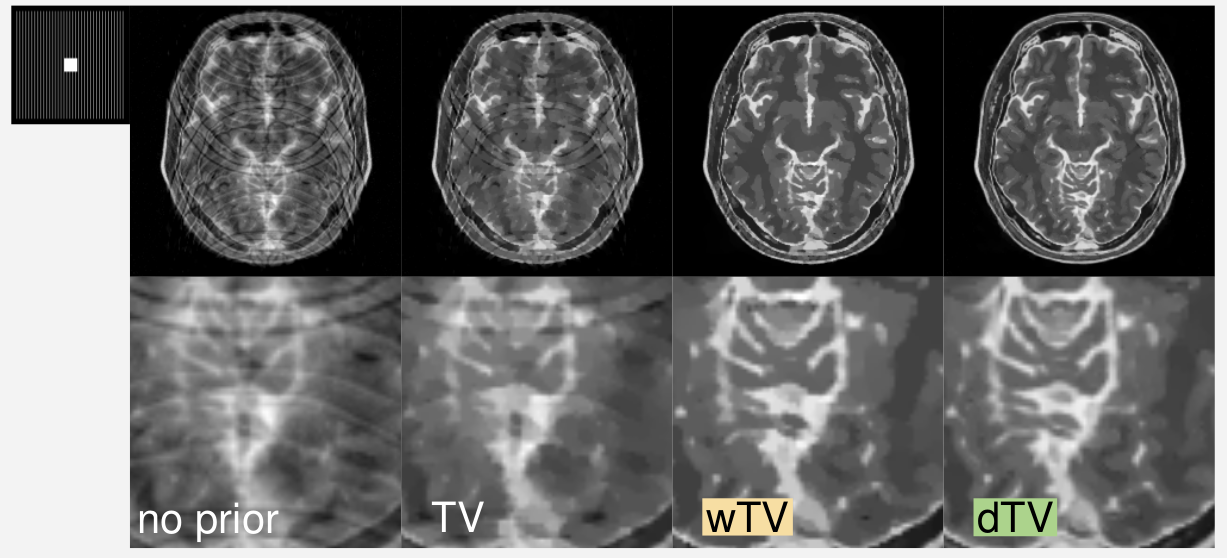 |
Reconstructions with different a priori knowledge. The reconstruction quality improves visually significantly from left to right.
Tested Configurations: The software was tested on Ubuntu 12.04 LTS with Matlab 2015a. If you have tested different configurations successfully please let me know m.j.ehrhardt@damtp.cam.ac.uk. Please also report me in the case of failure.
Reference: M. J. Ehrhardt and M. M. Betcke, Multi-Contrast MRI Reconstruction with Structure-Guided Total Variation, SIAM Journal on Imaging Sciences 9(3), pp. 1084?1106, 2016
Acknowledgements: The simulation results are based on BrainWeb data and patient data kindly provided by Ninon Burgos and Jonathan Schott from the University College London, UK.
Diffusion tensor imaging with deterministic error bounds [link to software] [download software (9 MB)]
Abstract: Errors in the data and the forward operator of an inverse problem can be handily modelled using partial order in Banach lattices. We present some existing results of the theory of regularisation in this novel framework, where errors are represented as bounds by means of the appropriate partial order. We apply the theory to diffusion tensor imaging (DTI), where correct noise modelling is challenging: it involves the Rician distribution and the nonlinear Stejskal-Tanner equation. Linearisation of the latter in the statistical framework would complicate the noise model even further. We avoid this using the error bounds approach, which preserves simple error structure under monotone transformations.
Reference: (2016). Diffusion tensor imaging with deterministic error bounds. Journal of Mathematical Imaging and Vision
Acceleration of the PDHGM on strongly convex subspaces [link to software] [download software (3 MB)]
Abstract: We propose several variants of the primal-dual method due to Chambolle and Pock. Without requiring full strong convexity of the objective functions, our methods are accelerated on subspaces with strong convexity. This yields mixed rates, with respect to initialisation and with respect to the dual sequence, and the residual part of the primal sequence. We demonstrate the efficacy of the proposed methods on image processing problems lacking strong convexity, such as total generalised variation denoising and total variation deblurring.
Reference: Valkonen, T. & Pock, T. J Math Imaging Vis (2016). doi:10.1007/s10851-016-0692-2
Learning Filter Functions in Regularisers by Minimising Quotients [code (Apollo)] [paper (arXiv)]
Martin Benning, Guy Gilboa, Joana Sarah Grah, Carola-Bibiane Schönlieb
Abstract: Learning approaches have recently become very popular in the field of inverse problems. A large variety of methods has been established in recent years, ranging from bi-level learning to high-dimensional machine learning techniques. Most learning approaches, however, only aim at fitting parametrised models to favourable training data whilst ignoring misfit training data completely. In this paper, we follow up on the idea of learning parametrised regularisation functions by quotient minimisation as established in [2]. We extend the model therein to include higher-dimensiona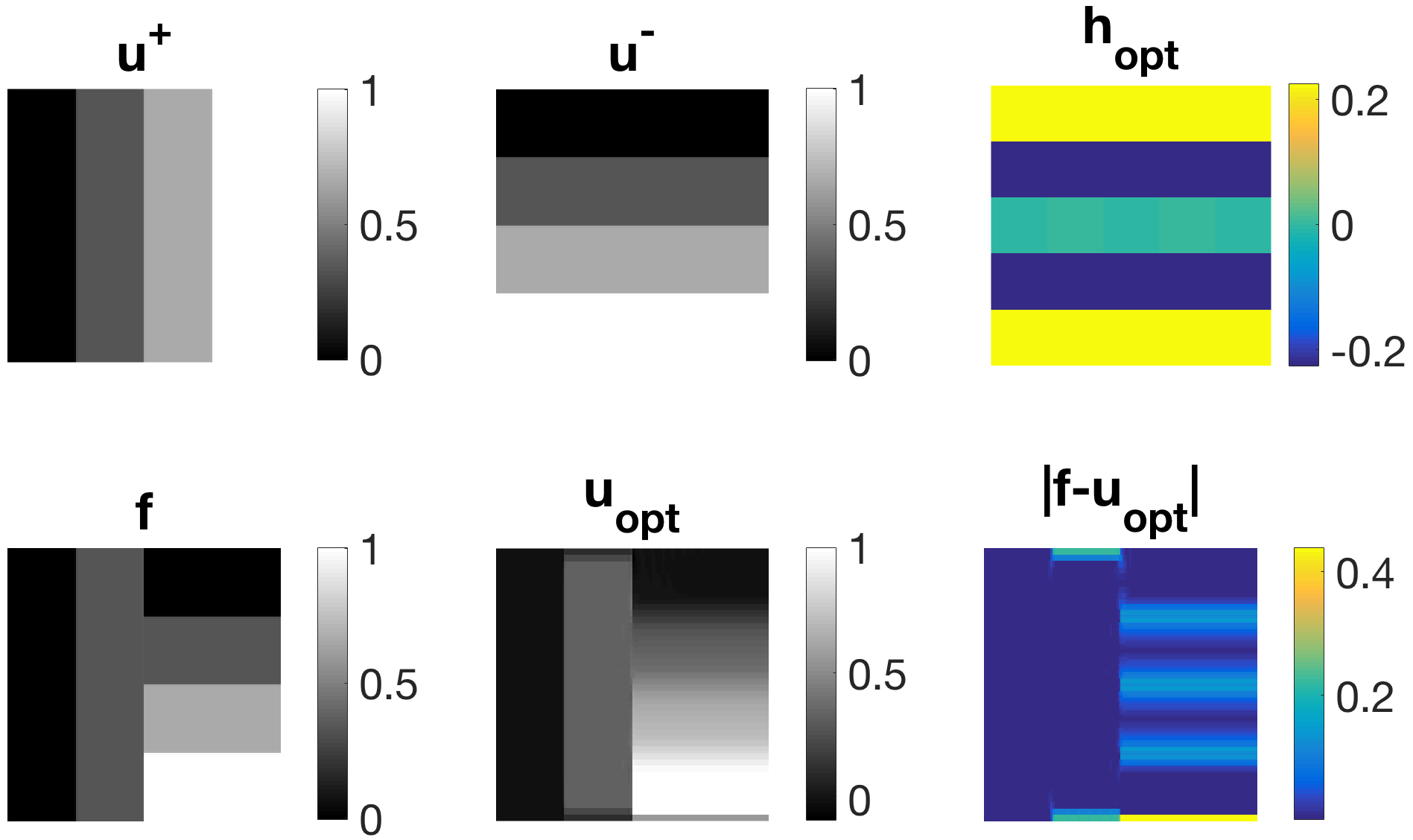 l filter functions to be learned and allow for fit- and misfit-training data consisting of multiple functions. We first present results resembling behaviour of well-established derivative-based sparse regularisers like total variation or higher-order total variation in one-dimension. Our second and main contribution is the introduction of novel families of non-derivative-based regularisers. This is accomplished by learning favourable scales and geometric properties while at the same time avoiding unfavourable ones.
l filter functions to be learned and allow for fit- and misfit-training data consisting of multiple functions. We first present results resembling behaviour of well-established derivative-based sparse regularisers like total variation or higher-order total variation in one-dimension. Our second and main contribution is the introduction of novel families of non-derivative-based regularisers. This is accomplished by learning favourable scales and geometric properties while at the same time avoiding unfavourable ones.
Reference: [1] Martin Benning, Guy Gilboa, Joana Sarah Grah and Carola-Bibiane Schönlieb. "Learning Filter Functions in Regularisers by Minimising Quotients." Scale Space and Variational Methods in Computer Vision (2017), accepted.
[2] Martin Benning, Guy Gilboa, and Carola?Bibiane Schönlieb. "Learning parametrised regularisation functions via quotient minimisation." PAMM 16.1 (2016): 933-936.
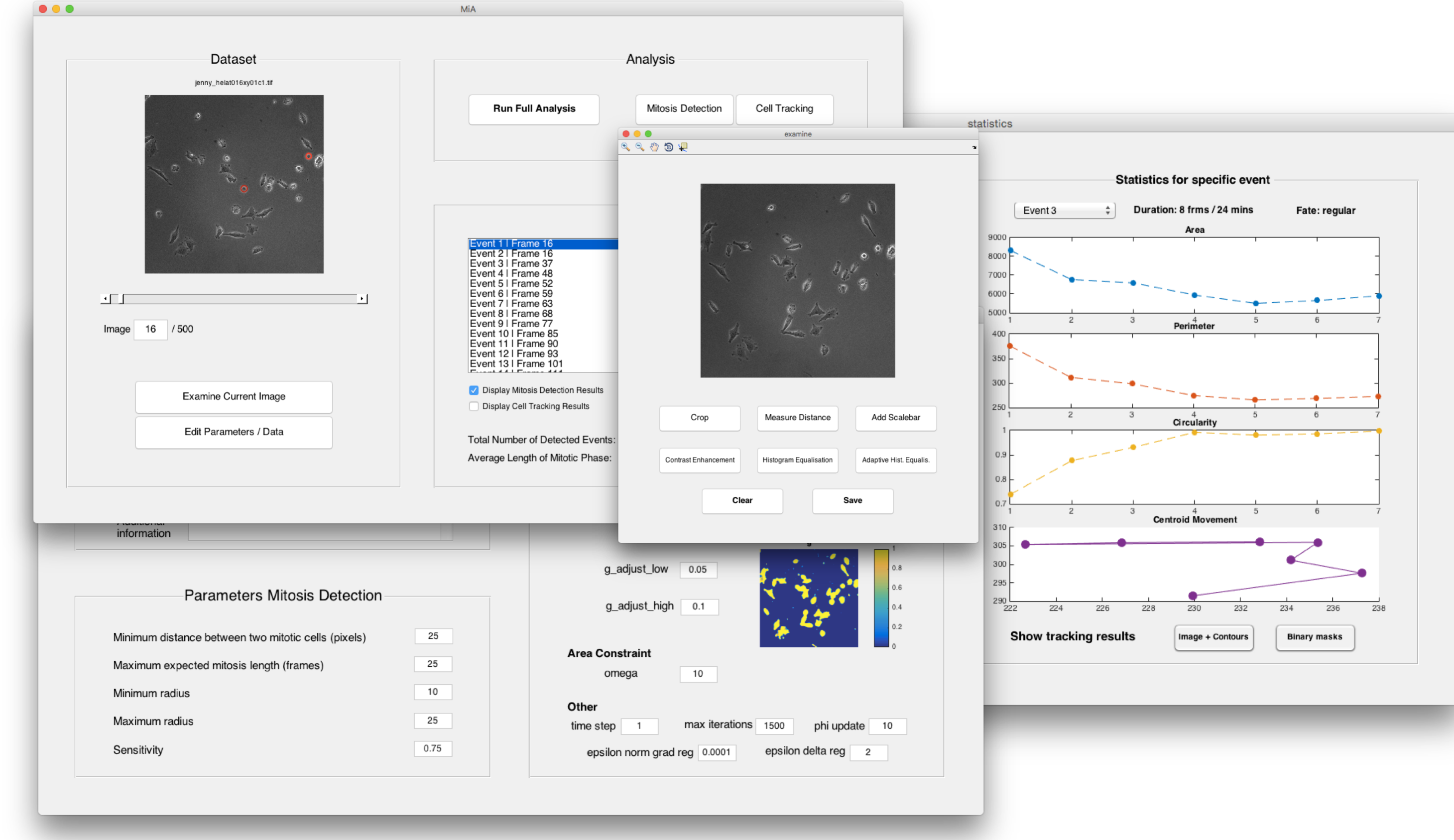
Mathematical Imaging Methods for Mitosis Analysis in Live-Cell Phase Contrast Microscopy [code (GitHub)] [paper (DOI) (arXiv)]
Joana Sarah Grah, Jennifer Alison Harrington, Siang Boon Koh, Jeremy Andrew Pike, Alexander Schreiner, Martin Burger, Carola-Bibiane Schönlieb, Stefanie Reichelt
Abstract: We propose a workflow to detect and track mitotic cells in time-lapse microscopy image sequences. In order to avoid the requirement for cell lines expressing fluorescent markers and the associated phototoxicity, phase contrast microscopy is often preferred over fluorescence microscopy in live-cell imaging. However, common specific image characteristics complicate image processing and impede use of standard methods. Nevertheless, automated analysis is desirable due to manual analysis being subjective, biased and extremely time-consuming for large data sets. Here, we present the following workflow based on mathematical imaging methods. In the first step, mitosis detection is performed by means of the circular Hough transform. The obtained circular contour subsequently serves as an initialisation for the tracking algorithm based on variational methods. It is sub-divided into two parts: in order to determine the beginning of the whole mitosis cycle, a backwards tracking procedure is performed. After that, the cell is tracked forwards in time until the end of mitosis. As a result, the average of mitosis duration and ratios of different cell fates (cell death, no division, division into two or more daughter cells) can be measured and statistics on cell morphologies can be obtained. All of the tools are featured in the user-friendly MATLAB® Graphical User Interface MitosisAnalyser.
|
|
Reference: Joana Sarah Grah, Jennifer Alison Harrington, Siang Boon Koh, Jeremy Andrew Pike, Alexander Schreiner, Martin Burger, Carola-Bibiane Schönlieb, Stefanie Reichelt. "Mathematical imaging methods for mitosis analysis in live-cell phase contrast microscopy." Methods 115 (2017): 91-99.

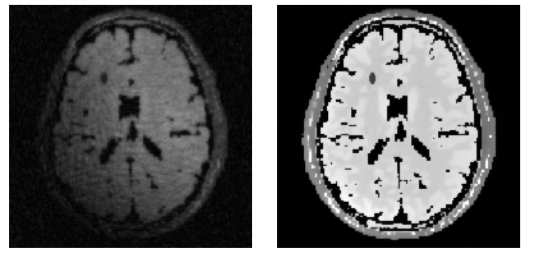
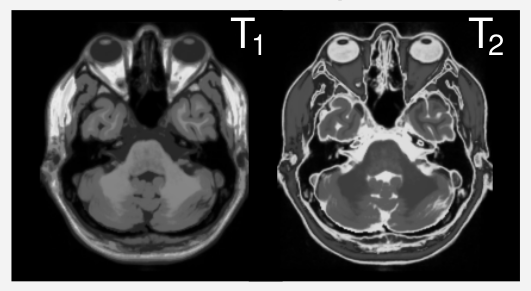 Different scan parameters lead to different contrasts in MRI.
Different scan parameters lead to different contrasts in MRI.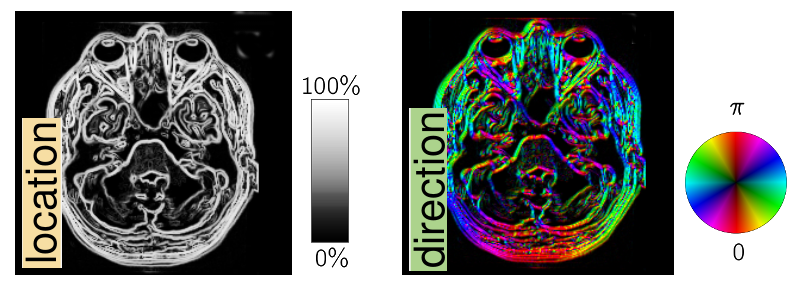 Structure can be either based on the location or direction of edges.
Structure can be either based on the location or direction of edges.