University of Cambridge, DAMTP: Quantum Fluids Laboratory Berloff

University of Cambridge > DAMTP > Quantum Fluids > Research

Overview

Our group seeks to understand fundamental principles that govern the behavior of nonequilibrium coherent systems in physics and how these principles may lead to physics-inspired algorithms and physics-based analogue computing. The key to understanding the universal behaviour of such systems lies in the common description obtained when particular microscopic models are reduced to order parameter equations. Universal order parameter equations written for complex matter fields are widely used to describe systems as different as Bose-Einstein condensates of ultra cold atomic gases, thermal convection, nematic liquid crystals, solid-state condensates, lasers and other nonlinear systems.
Our focus is on modelling coherent nonequilibrium systems such as Bose Condensation of excitons and polaritons, magnons, atomic gases, superfluid helium and understanding the dynamical behaviour of these systems.

More details of our research on physics-inspired computing can be found at Pi-Computing Research group website. The topics for PhD research n the area of pi-computing for 2024 can be found at PhD Projects page

Polariton Graph Simulator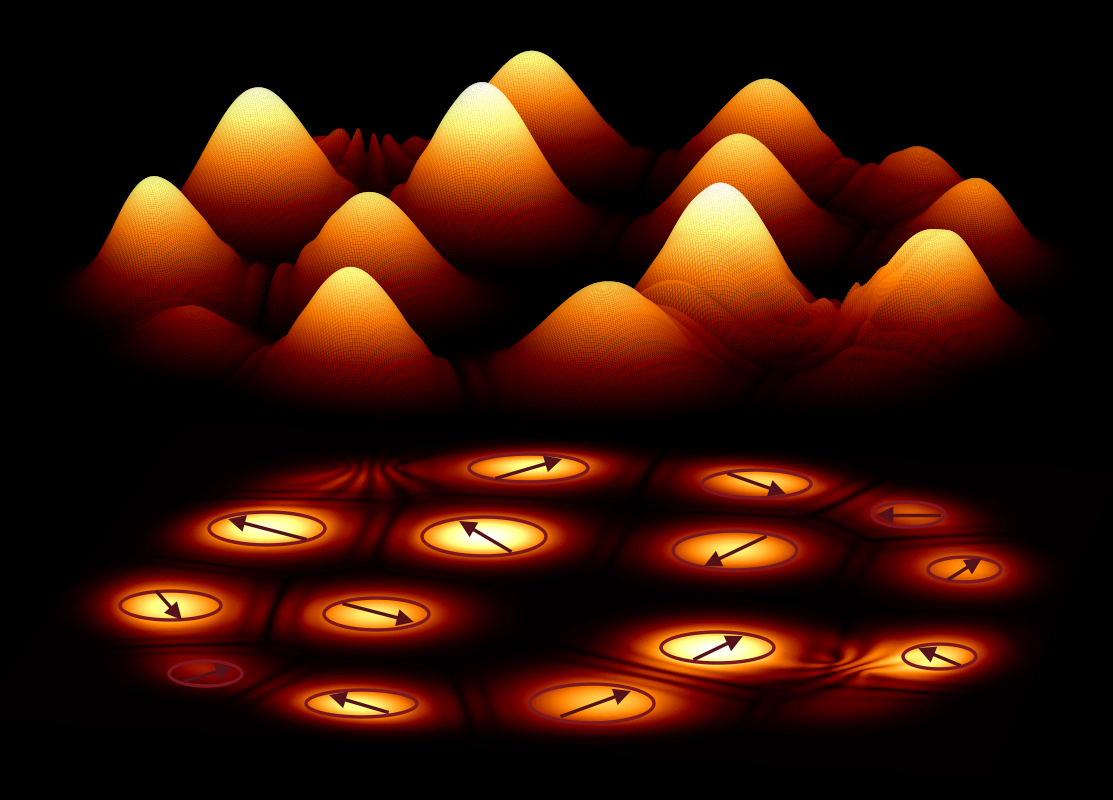

We have developed a Polariton Graph Simulator that acts as an analog simulator of hard optimization problems. Polariton graphs simulator is a novel platform for solving hard optimization problems that can be mapped into the XY model. Polariton condensates can be imprinted into any two-dimensional graph by spatial modulation of the pumping laser. By controlling the pumping intensity and profile, the graph geometry and the separation distance between the lattice sites one can control the couplings between the sites and realise various phase configurations that minimize the XY model. This gives rise to the use of the polariton graph as an analogue XY Hamiltonian simulator. The search for the global minimum of the XY Hamiltonian is via a bottom-up approach which has an advantage over classical or quantum annealing techniques, where the global ground state is reached through either a transition over metastable excited states or via tunnelling between the states in time that depends on the size of the system.

Hydrodynamics of Quantum Fluids

Quantum fluids have been studied experimentally for many years and have by now become a major focus of cryogenic physics. Applications of the subject are wide-ranging, from engineering (where, for instance, helium is used as a coolant for superconducting magnets and infrared detectors) to astrophysics (where it is invoked to explain glitches in the rotation of neutron stars). Superfluid turbulence may also provide insights into classical fluid turbulence, especially at high Reynolds numbers, where the vorticity has an intermittent, fractal character.

Even though the superfluid is inviscid, there are significant differences between classical turbulence at large Reynolds number and superfluid turbulence. The most significant is that vorticity is continuously distributed in a classical (Navier-Stokes) fluid, but is quantised in a superfluid in units of h/M, where M is the mass of the boson. Turbulence in the superfluid therefore resembles a tangle of vortex filaments, whose dynamics differs from that of the chaotic but continuous vorticity of classical turbulence.

We are interested in modelling, developing analytical approaches (asymptotic and perturbation methods) and applying numerical simulations in order to elucidate motions in Bose-Einstein condensates and superfluid helium.

Vortex Motion and Turbulence

One direction of our research is to relate and improve different mathematical models of superfluid turbulence by developing hierarchies of new stochastic models of vortex motion and turbulence. Mathematical models of superfluidity and superfluid turbulence have used four approaches: (1) the phenomenological Landau two-fluid model, (2) the phenomenological Hall-Vinen-Bekherevich-Khalatnikov (HVBK) model, (3) classical inviscid model of vortex motion with ad hoc reconnections, and (4) the Gross-Pitaevskii (GP) semi-classical model. The first of these was designed to describe the superfluid motion at all temperatures at which superfluidity exists. It requires modification when the vorticity is present. The HVBK model is intended for situations in which superfluid lines are dense. The GP model is applicable at very low temperatures where normal fluid is absent; it has proved its worth especially recently in describing dilute condensates.

Condensation of nonlinear waves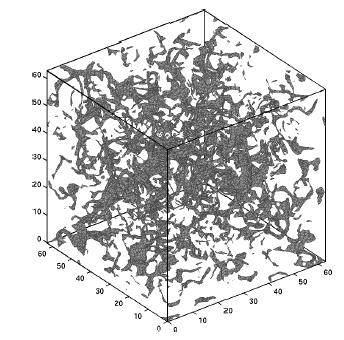

Many classical systems in nature reveal the emergence of large scale coherent structures from a background irregular field characterised by small-scale fluctuations. Examples of systems that exhibit such behaviour include classical turbulence, nonlinear optics, superfluids, ultracold gases and Bose-Einstein Condensates, and the formation of the early universe. We are interested in elucidating these processes for various condensate models and for more than one component. In certain regions of the parameter space, a large sub-class of these systems can be described by a system of weakly nonlinear dispersive waves that can be analysed to find analytical and universal solutions that describe the paths to condensation. (Image at right is copyright 2009 Elsevier: see H. Salmon and N.G. Berloff, Physica D, 238, 1482, 2009).

Finite Temperature BECs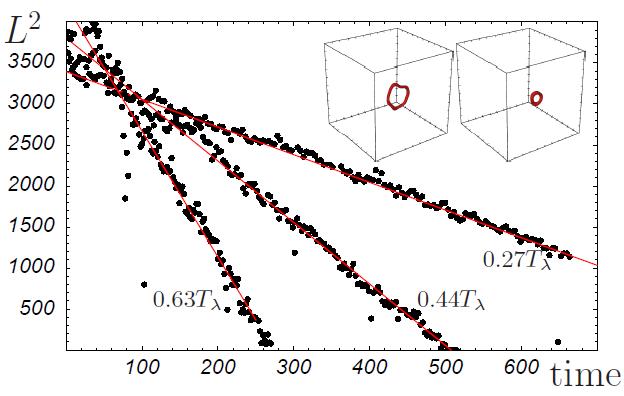

The problem of a vortex tangle interacting with the normal fluid (thermal cloud) is the key question in superfluid turbulence. The vortex lines create a force of mutual friction between superfluid and normal fluid in addition to the mutual friction included by Landau in his equations, and represents the effects of collisions of the quasiparticles with the vortex cores. We studied the effect of these collisions quantitatively and found that the vortex line decay law at non-zero temperature in the context of the defocusing NLS equation. (Image at left is from N. G. Berloff and A. J. Youd, Physical Review Letters, 99, 145301, 2007.)

Electron bubbles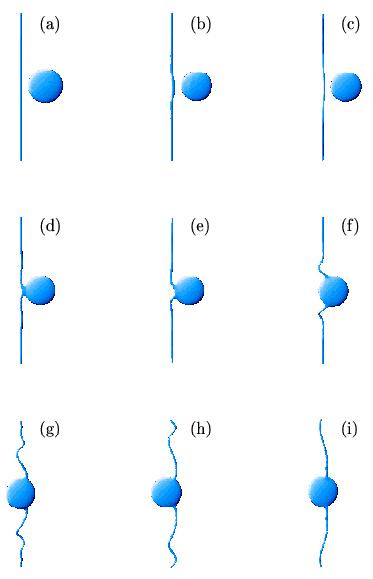

Much of what is known about vortices in superfluid helium is obtained from experiments using impurities as probes. These impurities are of three types: negative ions, which are electrons in relatively large (radius of 16 Å) bubbles cut out of the liquid owing to the repulsive interactions between helium atoms and electrons; positive ions such as 4He (8 Å); and neutral atoms such as 3He (4 Å). By modelling the coupled dynamics of the electron bubble and condensate we showed for the first time how the electron bubble is being trapped by a vortex line. The trapping of impurities is now used widely to study the structure of turbulent vortex tangle. (Image at right is from N.G. Berloff and P.H. Roberts, Phys. Rev. B, 63, 024510, 2000)

Exciton-polariton condensates

Microcavity exciton-polaritons are quasi-particles that result from the hybridisation of excitons (bound electron hole pairs) and light confined inside semiconductor microcavities. At low enough densities, they behave as bosons according to Bose-Einstein statistics, and so one may investigate Bose-Einstein condensation of these particles, and the phenomena associated with it, such as increased coherence, superfluidity and quantised vortices. Because of the imperfect confinement of the photon component, exciton-polaritons have a finite lifetime, and have to be continuously re-populated. These systems are therefore capable of pattern forming and the studies of the conditions and the instabilities that lead to various pattern is a direction of our research. (Image at right is from J. Keeling and N.G. Berloff, Phys. Rev. Lett 100, 250401, 2008 showing spontaneous formation of a rotating vortex lattice in a pumped decaying condensate in the absence of any external rotation.)

Spinor condensates

Microcavity polaritons also possess the spin degree of freedom. One of the directions of our research is to model and investigate the rich varieties of behavior that come from combining spatial profiles driven by particle flow with the dynamics due to the spin degree of freedom in exciton-polariton condensates. (Image at right is adapted from M. O. Borgh, J. Keeling and N.G. Berloff, Phys. Rev. B 81, 235302, 2010 and illustrate nonuniform interconversion between two spinor components.)

Other solid-state condensates

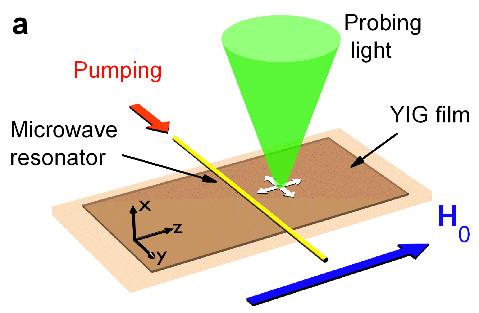Other solid-state condensates, such as magnon condesates are subject of our research. Magnons are elementary excitations -- quantised spin waves -- of a magnetic system have been observed to condense in ferromagnets, in superfluid 3He-B and in compressed aerogel of superfluid 3He-A. Similar to the phases of non-condensed Bose gas, atomic spins of normal magnetic materials are in a disordered paramagnetic state. In the ordered state the spins develop the common global frequency and phase of precession. The magnon condensation of room temperature yttrium-iron garnet (YIG) films magnetised by in-plane fields is driven by microwave radiation. A microwave photon excites two primary magnons that relax forming a magnon gas with the Bose distribution. The chemical potential increases with pumping power. When the microwave power exceeds a threshold value, the magnon population condenses at finite minima of the dispersion spectrum formed by the combined effects of the exchange and magnetic dipolar interactions. We are interested in modelling these condensates and understanding the structure of the ground state and excitations such as vortices and sound waves. (Image at left is adapted from P. Nowik-Boltyk, O. Dzyapko, V. E. Demidov, N.G. Berloff and S. O. Demokritov "Doubly degenerate Bose-Einstein condensate of magnons: spatially non-uniform ground state and pairs of quantized vortices", Nature Sci. Reps., 2, 482(2012))

Universality of condensate systems

We are interested in drawing analogies and understanding generelities between lasers, solid-state-non-equilibrium condensates and equilibrium condensates. There exists a number of universal equations which describe various regimes of the dynamics of non-equilibrium condensates: the Gross-Pitaevskii equation for weakly interacting equilibrium condensates, the complex Ginsburg-Landau equation and the complex Swift-Hohenberg equation that is used to model lasers. All these equations can be derived asymptotically from a generic laser model given by Maxwell-Bloch equations. Such an universal framework allows the unified treatment of various systems and continuously cross from one system to another.

RETUNE 2012: Relaxation, Turbulence, and Non-Equilibrium Dynamics of Matter Fields - From Quantum Fluids to High-Energy Physics -