2 My First Path Integral

It’s now time to understand a little better how to deal with the path integral

\displaystyle Z=\int{\cal D}m({{\bf x}})\ e^{-\beta F[m({{\bf x}})]}

(2.34)

Our strategy – at least for now – will be to work in situations where the saddle point dominates, with the integral giving small corrections to this result. In this regime, we can think of the integral as describing the thermal fluctuations of the order parameter $m({{\bf x}})$ around the equilibrium configuration determined by the saddle point. As we will see, this approach fails to work at the critical point, which is the regime we’re most interested in. We will then have to search for other techniques, which we will describe in Section 3.

Preparing the Scene

Before we get going, we’re going to change notation. First, we will change the name of our main character and write the magnetisation as

\displaystyle m({\bf x})\ \rightarrow\ \phi({\bf x})

If you want a reason for this, I could tell you that the change of name is in deference to universality and the fact that the field could describe many things, not just magnetisation. But the real reason is simply that fields in path integrals should have names like $\phi$ . (This is especially true in quantum field theory where $m$ is reserved for the mass of the particle.)

We start by setting $B=0$ ; we’ll turn $B$ back on in Section 2.2. The free energy is then

\displaystyle F[\phi({{\bf x}})]=\int d^{d}x\ \left[\frac{1}{2}\alpha_{2}(T)% \phi^{2}+\frac{1}{4}\alpha_{4}(T)\phi^{4}+\frac{1}{2}\gamma(T)(\nabla\phi)^{2}% +\ldots\right]

Roughly speaking, path integrals are trivial to do if $F[\phi({{\bf x}})]$ is quadratic in $\phi$ , and possible to do if the higher order terms in $F[\phi({{\bf x}})]$ give small corrections. If the higher order terms in $F[\phi({{\bf x}})]$ are important, then the path integral is typically impossible without the use of numerics. Here we’ll start with the trivial, building up to the “possible” in later chapters.

To this end, throughout the rest of this chapter we will restrict attention to a free energy that contains no terms higher than quadratic in $\phi({{\bf x}})$ . We have to be a little careful about whether we sit above or below the critical temperature. When $T>T_{c}$ , things are easy and we simply throw away all higher terms and work with

\displaystyle F[\phi({{\bf x}})]=\frac{1}{2}\int d^{d}x\ \left(\gamma\nabla% \phi\cdot\nabla\phi+\mu^{2}\phi^{2}\right)

(2.35)

where $\mu^{2}=\alpha_{2}(T)$ is positive.

A word of caution. We are ignoring the quartic terms purely on grounds of expediency: this makes our life simple. However, these terms become increasingly important as $\mu^{2}\sim\alpha_{2}(T)\rightarrow 0$ and we approach the critical point. This means that nothing we are about to do can be trusted near the the critical point. Nonetheless, we will be able to extract some useful intuition from what follows. We will then be well armed to study critical phenomena in Section 3.

When $T<T_{c}$ , and $\alpha_{2}(T)<0$ , we need to do a little more work. Now the saddle point does not lie at $\phi=0$ , but rather at $\langle\phi\rangle=\pm m_{0}$ given in (1.31). In particular, it’s crucial that we keep the quartic term because this rescues the field from the upturned potential it feels at the origin.

However, it’s straightforward to take this into account. We simply compute the path integral about the appropriate minimum by writing

\displaystyle\tilde{\phi}({\bf x})=\phi({{\bf x}})-\langle\phi\rangle

(2.36)

Substituting this into the free energy gives

\displaystyle F[\tilde{\phi}({\bf x})]=F[m_{0}]+\frac{1}{2}\int d^{d}x\left[% \alpha_{2}^{\prime}(T)\tilde{\phi}^{2}+\gamma(T)(\nabla\tilde{\phi})^{2}+% \ldots\right]

(2.37)

where now the $\ldots$ include terms of order $\tilde{\phi}^{3}$ and $\tilde{\phi}^{4}$ and higher, all of which we’ve truncated. Importantly, there are no terms linear in $\tilde{\phi}$ . In fact, this was guaranteed to happen: the vanishing of the linear terms is equivalent to the requirement that the equation of motion (1.30) is obeyed. The new quadratic coefficient is

\displaystyle\alpha_{2}^{\prime}(T)=\alpha_{2}(T)+3m_{0}^{2}\alpha_{4}(T)=-2% \alpha_{2}(T)

(2.38)

In particular, $\alpha_{2}^{\prime}(T)>0$ .

Practically, this means that we take the calculations that we do at $T>T_{c}$ with the free energy (2.35) and trivially translate them into calculations at $T<T_{c}$ . We just need to remember that we’re working with a shifted $\phi$ field, and that we should take $\mu^{2}=\alpha^{\prime}_{2}(T)=|2\alpha_{2}(T)|$ . Once again, the same caveats hold: our calculations should not be trusted near the critical point $\mu^{2}=0$ .

2.1 The Thermodynamic Free Energy Revisited

For our first application of the path integral, we will compute something straightforward and a little bit boring: the thermodynamic free energy. There will be a little insight to be had from the result of this, although the main purpose of going through these steps is to prepare us for what’s to come.

We’ve already found some contributions to the thermodynamic free energy. There is the constant term $F_{0}(T)$ and, if we’re working at $T<T_{c}$ , the additional contribution $F[m_{0}]$ in (2.37). Here we are interested in further contributions to $F_{\rm thermo}$ , coming from fluctuations of the field. To keep the formulae simple, we will ignore these two earlier contributions; you can always put them back in if you please.

Throughout this calculation, we’ll set $B=0$ so we’re working with the free energy (2.35). There is a simple trick to compute the partition function when the free energy is quadratic: we work in Fourier space. We write the Fourier transform of the magnetisation field as

\displaystyle\phi_{\bf k}=\int d^{d}x\ e^{-i{\bf k}\cdot{\bf x}}\,\phi({{\bf x% }})

Since our original field $\phi({{\bf x}})$ is real, the Fourier modes obeys $\phi_{\bf k}^{\star}=\phi_{-{\bf k}}$ .

The ${\bf k}$ are wavevectors. Following the terminology of quantum mechanics, we will refer to ${\bf k}$ as the momentum. At this stage, we should remember something about our roots. Although we’re thinking of $\phi({{\bf x}})$ as a continuous field, ultimately it arose from a lattice and so can’t vary on very small distance scales. This means that the Fourier modes must all vanish for suitably high momentum,

\displaystyle\phi_{\bf k}=0\ \ \ {\rm for}\ |{\bf k}|>\Lambda

Here $\Lambda$ is called the ultra-violet (UV) cut-off. In the present case, we can think of $\Lambda=\pi/a$ , with $a$ the distance between the boxes that we used to coarse grain when first defining $\phi({{\bf x}})$ .

We can recover our original field by the inverse Fourier transform. It’s useful to have two different scenarios in mind. In the first, we place the system in a finite spatial volume $V=L^{d}$ . In this case, the momenta take discrete values,

\displaystyle{\bf k}=\frac{2\pi}{L}{\bf n}\ \ \ \ \ \ {\bf n}\in{\bf Z}^{d}

(2.39)

and the inverse Fourier transform is

\displaystyle\phi({{\bf x}})=\frac{1}{V}\sum_{{\bf k}}e^{i{\bf k}\cdot{\bf x}}% \,\phi_{\bf k}

(2.40)

Alternatively, if we send $V\rightarrow\infty$ , the sum over ${\bf k}$ modes becomes an integral and we have

\displaystyle\phi({{\bf x}})=\int\frac{d^{d}k}{(2\pi)^{d}}e^{i{\bf k}\cdot{\bf x% }}\,\phi_{\bf k}

(2.41)

In what follows, we’ll jump backwards and forwards between these two forms. Ultimately, we will favour the integral form. But there are times when it will be simpler to think of the system in a finite volume as it will make us less queasy about some of the formulae we’ll encounter.

For now, let’s work with the form (2.41). We substitute this into the free energy to find

\displaystyle F[\phi_{\bf k}]=\frac{1}{2}\int\frac{d^{d}k_{1}}{(2\pi)^{d}}% \frac{d^{d}k_{2}}{(2\pi)^{d}}\int d^{d}x\ \left(-\gamma{\bf k}_{1}\cdot{\bf k}% _{2}+\mu^{2}\right)\phi_{{\bf k}_{1}}\phi_{{\bf k}_{2}}\,e^{i({\bf k}_{1}+{\bf k% }_{2})\cdot{\bf x}}

The integral over ${\bf x}$ is now straightforward and gives us a delta function

\displaystyle\int d^{d}x\ e^{i({\bf k}_{1}+{\bf k}_{2})\cdot{\bf x}}=(2\pi)^{d% }\delta^{d}({\bf k}_{1}+{\bf k}_{2})

and the free energy takes the simple form

\displaystyle F[\phi_{\bf k}]=\frac{1}{2}\int\frac{d^{d}k}{(2\pi)^{d}}\ \left(% \gamma k^{2}+\mu^{2}\right)\phi_{\bf k}\phi_{-{\bf k}}=\frac{1}{2}\int\frac{d^% {d}k}{(2\pi)^{d}}\ \left(\gamma k^{2}+\mu^{2}\right)\phi_{\bf k}\phi^{\star}_{% {\bf k}}

(2.42)

Now we can see the benefit of working in Fourier space: at quadratic order, the free energy decomposes into individual $\phi_{\bf k}$ modes. This is because the Fourier basis is the eigenbasis of $-\gamma\nabla^{2}+\mu^{2}$ , allowing us to diagonalise this operator.

To perform the functional integral, we also need to change the measure. Recall that the path integral was originally an integral over $\phi({{\bf x}})$ for each value of ${\bf x}$ labelling the position of a box. Now it is an integral over all Fourier modes, which we write as

\displaystyle\int{\cal D}\phi({{\bf x}})=\prod_{\bf k}\left[\,{\cal N}\!\int d% \phi_{\bf k}d\phi^{\star}_{\bf k}\right]

(2.43)

where we should remember that $\phi^{\star}_{\bf k}=\phi_{-{\bf k}}$ because $\phi({\bf x})$ is real. I’ve included a normalisation constant ${\cal N}$ in this measure. I’ll make no attempt to calculate this and, ultimately, it won’t play any role because, having computed the partition function, the first thing we do is take the log and differentiate. At this point, ${\cal N}$ will drop out. In later formulae, we’ll simply ignore it. But it’s worth keeping it in for now.

Our path integral is now

\displaystyle Z=\prod_{{\bf k}}\,{\cal N}\!\int d\phi_{\bf k}d\phi_{\bf k}^{% \star}\ \exp\left(-\frac{\beta}{2}\int\frac{d^{d}k}{(2\pi)^{d}}\ \left(\gamma k% ^{2}+\mu^{2}\right)|\phi_{\bf k}|^{2}\right)

If this still looks daunting, we just need to recall that in finite volume, the integral in the exponent is really a sum over discrete momentum values,

	$\displaystyle Z$	$\displaystyle=$	$\displaystyle\prod_{{\bf k}}\,{\cal N}\!\int d\phi_{\bf k}d\phi_{\bf k}^{\star% }\ \exp\left(-\frac{\beta}{2V}\sum_{\bf k}\ \left(\gamma k^{2}+\mu^{2}\right)\|% \phi_{\bf k}\|^{2}\right)$
		$\displaystyle=$	$\displaystyle\prod_{{\bf k}}\left[{\cal N}\int d\phi_{\bf k}d\phi_{\bf k}^{% \star}\ \exp\left(-\frac{\beta}{2V}\left(\gamma k^{2}+\mu^{2}\right)\|\phi_{\bf k% }\|^{2}\right)\right]$

Note that the placement of brackets shifted in the two lines, because the sum in the exponent got absorbed into the overall product. If this is confusing, it might be worth comparing what we’ve done above to a simple integral of the form $\int dx\,dy\ e^{-x^{2}-y^{2}}=(\int dx\ e^{-x^{2}})(\int dy\ e^{-y^{2}})$ .

We’re left with something very straightforward: it’s simply a bunch of decoupled Gaussian integrals, one for each value of ${\bf k}$ . Recall that Gaussian integral over a single variable is given by

\displaystyle\int_{-\infty}^{+\infty}dx\ e^{-x^{2}/2a}=\sqrt{2\pi a}

(2.44)

Applying this for each ${\bf k}$ , we have our expression for the path integral

\displaystyle Z=\prod_{\bf k}{\cal N}\sqrt{\frac{2\pi TV}{\gamma k^{2}+\mu^{2}}}

where the square root is there, despite the fact that we’re integrating over complex $\phi_{\bf k}$ , because $\phi_{\bf k}^{\star}=\phi_{-{\bf k}}$ is not an independent variable. Note that we have a product over all ${{\bf k}}$ . In finite volume, where the possible ${\bf k}$ are discrete, there’s nothing fishy going on. But as we go to infinite volume, this will become a product over a continuous variable ${\bf k}$ .

We can now compute the contribution of these thermal fluctuations to the thermodynamic free energy. The free energy per unit volume is given by $Z=e^{-\beta F_{\rm thermo}}$ or,

\displaystyle\frac{F_{\rm thermo}}{V}=-\frac{T}{V}\log Z=-\frac{T}{2V}\sum_{{% \bf k}}\,\log\left(\frac{2\pi TV{\cal N}^{2}}{\gamma k^{2}+\mu^{2}}\right)

We can now revert back to the integral over ${\bf k}$ , rather than the sum by writing

\displaystyle\frac{F_{\rm thermo}}{V}=-\frac{T}{2}\int\frac{d^{d}k}{(2\pi)^{d}% }\log\left(\frac{2\pi TV{\cal N}^{2}}{\gamma k^{2}+\mu^{2}}\right)

This final equation might make you uneasy since there an explicit factor of the volume $V$ remains in the argument, but we’ve sent $V\rightarrow\infty$ to convert from $\sum_{\bf k}$ to $\int d^{d}k$ . At this point, the normalisation factor ${\cal N}$ will ride to the rescue. However, as advertised previously, none of these issues are particularly important since they drop out when we compute physical quantities. Let’s look at the simplest example.

2.1.1 The Heat Capacity

Our real interest lies in the heat capacity per unit volume, $c=C/V$ . Specifically, we would like to understand the temperature dependence of the heat capacity. This is given by (1.15),

\displaystyle c=\frac{\beta^{2}}{V}\frac{\partial^{2}}{\partial\beta^{2}}\log Z% =\frac{1}{2}\left(T^{2}\frac{\partial{}}{\partial{T^{2}}}+2T\frac{\partial{}}{% \partial{T}}\right)\int\frac{d^{d}k}{(2\pi)^{d}}\log\left(\frac{2\pi TV{\cal N% }^{2}}{\gamma k^{2}+\mu^{2}}\right)

The derivatives hit both the factor of $T$ in the numerator, and any $T$ dependence in the coefficients $\gamma$ and $\mu^{2}$ . For simplicity, let’s work at $T>T_{c}$ . We’ll take $\gamma$ constant and $\mu^{2}=T-T_{c}$ . A little bit of algebra shows that the contribution to the heat capacity from the fluctuations is given by

\displaystyle c=\frac{1}{2}\int\frac{d^{d}k}{(2\pi)^{d}}\left[1-\frac{2T}{% \gamma k^{2}+\mu^{2}}+\frac{T^{2}}{(\gamma k^{2}+\mu^{2})^{2}}\right]

(2.45)

The first of these terms has a straightforward interpretation: it is the usual “ $\frac{1}{2}k_{B}$ ” per degree of freedom that we expect from equipartition, albeit with $k_{B}=1$ . (This can be traced to the original $\beta$ in $e^{-\beta F}$ .)

The other two terms come from the temperature dependence in $F[\phi({{\bf x}})]$ . What happens next depends on the dimension $d$ . Let’s look at the middle term, proportional to

\displaystyle\int_{0}^{\Lambda}dk\ \frac{k^{d-1}}{\gamma k^{2}+\mu^{2}}

For $d\geq 2$ , this integral diverges as we remove the UV cut-off $\Lambda$ . In contrast, when $d=1$ it is finite as $\Lambda\rightarrow\infty$ . When it is finite, we can easily determine the leading order temperature dependence of the integral by rescaling variables. We learn that

\displaystyle\int_{0}^{\Lambda}dk\ \frac{k^{d-1}}{\gamma k^{2}+\mu^{2}}\sim% \left\{\begin{array}[]{cc}\Lambda^{d-2}&{\rm when}\ d\geq 2\\ 1/\mu&{\rm when}\ d=1\end{array}\right.

(2.46)

When $d=2$ , the term $\Lambda^{0}$ should be replaced by a logarithm. Similarly, the final term in (2.45) is proportional to

\displaystyle\int_{0}^{\Lambda}dk\ \frac{k^{d-1}}{(\gamma k^{2}+\mu^{2})^{2}}% \sim\left\{\begin{array}[]{cc}\Lambda^{d-4}&{\rm when}\ d\geq 4\\ \mu^{d-4}&{\rm when}\ d<4\end{array}\right.

again, with a logarithm when $d=4$ .

What should we take from this? When $d\geq 4$ , the leading contribution to the heat capacity involves a temperature independent constant, $\Lambda$ , albeit a large one. This constant will be the same on both sides of the transition. (The heat capacity itself is not quite temperature independent as it comes with the factor of $T^{2}$ from the numerator of (2.45), but this doesn’t do anything particularly dramatic.) In contrast, when $d<4$ , the leading order contribution to the heat capacity is proportional to $\mu^{d-4}$ . And, this leads to something more interesting.

To see this interesting behaviour, we have to do something naughty. Remember that our calculation above isn’t valid near the critical point, $\mu^{2}=0$ , because we’ve ignored the quartic term in the free energy. Suppose, however, that we throw caution to the wind and apply our result here anyway. We learn that, for $d<4$ , the heat capacity diverges at the critical point. The leading order behaviour is

\displaystyle c\sim|T-T_{c}|^{-\alpha}\ \ \ {\rm with}\ \alpha=2-\frac{d}{2}

(2.47)

This is to be contrasted with our mean field result which gives $\alpha=0$ .

As we’ve stressed, we can’t trust the result (2.47). And, indeed, this is not the right answer for the critical exponent. But it does give us some sense for how the mean field results can be changed by the path integral. It also gives a hint for why the critical exponents are not affected when $d\geq 4$ , which is the upper critical dimension.

2.2 Correlation Functions

The essential ingredient of Landau-Ginzburg theory – one that was lacking in the earlier Landau approach – is the existence of spatial structure. With the local order parameter $\phi({{\bf x}})$ , we can start to answer questions about how the magnetisation varies from point to point.

Such spatial variations exist even in the ground state of the system. Mean field theory – which is synonymous with the saddle point of the path integral – tells us that the expectation value of the magnetisation is constant in the ground state

\displaystyle\langle\phi({{\bf x}})\rangle=\left\{\begin{array}[]{cc}0&T>T_{c}% \\ \pm m_{0}&T<T_{c}\end{array}\right.

(2.48)

This makes us think of the ground state as a calm fluid, like the Cambridge mill pond when the tourists are out of town. This is misleading. The ground state is not a single field configuration but, as always in statistical mechanics, a sum over many possible configurations in the thermal ensemble. This is what the path integral does for us. The importance of these other configurations will determine whether the ground state is likely to contain only gentle ripples around the background (2.48), or fluctuations so wild that it makes little sense to talk about an underlying background at all.

These kind of spatial fluctuations of the ground state are captured by correlation functions. The simplest is the two-point function $\langle\phi({{\bf x}})\phi({\bf y})\rangle$ , computed using the probability distribution (1.26). This tells us how the magnetisation at point ${\bf x}$ is correlated with the magnetisation at ${\bf y}$ . If, for example, there is an unusually large fluctuation at ${\bf y}$ , what will the magnitude of the field most likely be at ${\bf x}$ ?

Because $\langle\phi({{\bf x}})\rangle$ takes different values above and below the transition, it is often more useful to compute the connected correlation function,

\displaystyle\langle\phi({{\bf x}})\phi({\bf y})\rangle_{c}=\langle\phi({{\bf x% }})\phi({\bf y})\rangle-\langle\phi\rangle^{2}

(2.49)

If you’re statistically inclined, this is sometimes called a cumulant of the random variable $\phi({{\bf x}})$ .

The path integral provides a particularly nice way to compute connected correlation functions of this kind. We consider the system in the presence of a magnetic field $B$ , but now allow $B({\bf x})$ to also vary in space. We take the free energy to be

\displaystyle F[\phi({{\bf x}})]=\int d^{d}x\ \left[\frac{\gamma}{2}(\nabla% \phi)^{2}+\frac{\mu^{2}}{2}\phi^{2}({\bf x})-B({\bf x})\phi({{\bf x}})\right]

(2.50)

We can now think of the partition function as a functional of $B({\bf x})$ .

\displaystyle Z[B({\bf x})]=\int{\cal D}\phi\ e^{-\beta F}

For what it’s worth, $Z[B({\bf x})]$ is related to the Legendre transform of $F[\phi({{\bf x}})]$ .

Now that $Z$ depends on the function $B({\bf x})$ it is a much richer and more complicated object. Indeed, it encodes all the information about the fluctuations of the theory. Consider, for example, the functional derivative of $\log Z$ ,

\displaystyle\frac{1}{\beta}\frac{\delta\log Z}{\delta B({\bf x})}=\frac{1}{% \beta Z}\frac{\delta Z}{\delta B({\bf x})}=\frac{1}{Z}\int{\cal D}\phi\ \phi({% {\bf x}})\,e^{-\beta F}=\langle\phi({{\bf x}})\rangle_{B}

Here I’ve put a subscript $B$ on $\langle\cdot\rangle_{B}$ to remind us that this is the expectation value computed in the presence of the magnetic field $B({\bf x})$ . If our real interest is in what happens as we approach the critical point, we can simply set $B=0$ .

Similarly, if we can take two derivatives of $\log Z$ . Now when the second derivative hits, it can either act on the exponent $e^{-\beta F}$ , or on the $1/Z$ factor in front. The upshot is that we get

\displaystyle\frac{1}{\beta^{2}}\frac{\delta^{2}\log Z}{\delta B({\bf x})% \delta B({\bf y})}=\frac{1}{\beta^{2}Z}\frac{\delta^{2}Z}{\delta B({\bf x})% \delta B({\bf y})}-\frac{1}{\beta^{2}Z^{2}}\frac{\delta Z}{\delta B({\bf x})}% \frac{\delta Z}{\delta B({\bf y})}

\displaystyle\frac{1}{\beta^{2}}\frac{\delta^{2}\log Z}{\delta B({\bf x})% \delta B({\bf y})}=\langle\phi({{\bf x}})\phi({\bf y})\rangle_{B}-\langle\phi(% {\bf x})\rangle_{B}\langle\phi({\bf y})\rangle_{B}

which is precisely the connected correlation function (2.49). In what follows, we’ll mostly work above the critical temperature so that $\langle\phi\rangle_{B=0}=0$ . In this case, we set $B=0$ to find

\displaystyle\frac{1}{\beta^{2}}\left.\frac{\delta^{2}\log Z}{\delta B({\bf x}% )\delta B({\bf y})}\right|_{B=0}=\ \langle\phi({\bf x})\phi({\bf y})\rangle

(2.51)

All that’s left is for us to compute the path integral $Z[B({\bf x})]$ .

2.2.1 The Gaussian Path Integral

As in our calculation of the thermodynamic free energy, we work in Fourier space. The free energy is now a generalisation of (2.42),

\displaystyle F[\phi_{\bf k}]=\int\frac{d^{d}k}{(2\pi)^{d}}\ \Big{[}\frac{1}{2% }\left(\gamma k^{2}+\mu^{2}\right)\phi_{\bf k}\phi_{-{\bf k}}-B_{-{\bf k}}\phi% _{\bf k}\Big{]}

where $B_{\bf k}$ are the Fourier modes of $B({\bf x})$ . To proceed, we complete the square, and define the shifted magnetisation

\displaystyle\hat{\phi}_{\bf k}=\phi_{k}-\frac{B_{\bf k}}{\gamma k^{2}+\mu^{2}}

We can then write the free energy as

\displaystyle F[\hat{\phi}_{\bf k}]=\int\frac{d^{d}k}{(2\pi)^{d}}\ \left[\frac% {1}{2}\left(\gamma k^{2}+\mu^{2}\right)|\hat{\phi}_{\bf k}|^{2}-\frac{1}{2}% \frac{|B_{{\bf k}}|^{2}}{\gamma k^{2}+\mu^{2}}\right]

Our path integral is

\displaystyle Z=\prod_{k}\int d\hat{\phi}_{\bf k}d\hat{\phi}^{\star}_{\bf k}\ % e^{-\beta F[\hat{\phi}_{\bf k}]}

where we’ve shifted the integration variable from $\phi_{\bf k}$ to $\hat{\phi}_{\bf k}$ ; there is no Jacobian penalty for doing this. We’ve also dropped the normalisation constant ${\cal N}$ that we included in our previous measure (2.43) on the grounds that it clutters equations and does nothing useful.

The path integral now gives

\displaystyle Z[B({\bf x})]=e^{-\beta F_{\rm thermo}}\,\exp\left(\frac{\beta}{% 2}\int\frac{d^{d}k}{(2\pi)^{d}}\ \frac{|B_{{\bf k}}|^{2}}{\gamma k^{2}+\mu^{2}% }\right)

The first term $e^{-\beta F_{\rm thermo}}$ is just the contribution we saw before. It does not depend on the magnetic field $B({\bf x})$ and won’t contribute to the correlation function. (Specifically, it will drop out when we differentiate $\log Z$ .) The interesting piece is the dependence on the Fourier modes $B_{\bf k}$ . To get back to real space $B({\bf x})$ , we simply need to do an inverse Fourier transform. We have

\displaystyle Z[B({\bf x})]=e^{-\beta F_{\rm thermo}}\,\exp\left(\frac{\beta}{% 2}\int d^{d}xd^{d}y\ B({\bf x}){G}({\bf x}-{\bf y})B({\bf y})\right)

(2.52)

where

\displaystyle{G}({\bf x})=\int\frac{d^{d}k}{(2\pi)^{d}}\frac{e^{-i{\bf k}\cdot% {\bf x}}}{\gamma k^{2}+\mu^{2}}

(2.53)

We’re getting there. Differentiating the partition function as in (2.51), we learn that the connected two-point function is

\displaystyle\langle\phi({{\bf x}})\phi({\bf y})\rangle=\frac{1}{\beta}\,{G}({% \bf x}-{\bf y})

(2.54)

We just need to do the integral (2.53).

Computing the Fourier Integral

To start, note that the integral $G({\bf x})$ is rotationally invariant, and so $G({\bf x})=G(r)$ with $r=|{\bf x}|$ . We write the integral as

\displaystyle{G}(r)=\frac{1}{\gamma}\int\frac{d^{d}k}{(2\pi)^{d}}\frac{e^{-i{% \bf k}\cdot{\bf x}}}{k^{2}+1/\xi^{2}}

where we’ve introduced a length scale

\displaystyle\xi^{2}=\frac{\gamma}{\mu^{2}}

(2.55)

This is called the correlation length and it will prove to be important as we move forwards. We’ll discuss it more in Section 2.2.3.

To proceed, we use a trick. We can write

\displaystyle\frac{1}{k^{2}+1/\xi^{2}}=\int_{0}^{\infty}dt\ e^{-t(k^{2}+1/\xi^% {2})}

Using this, we have

$\displaystyle{G}(r)$	$\displaystyle=$	$\displaystyle\frac{1}{\gamma}\int\frac{d^{d}k}{(2\pi)^{d}}\int_{0}^{\infty}dt% \ e^{-i{\bf k}\cdot{\bf x}-t(k^{2}+1/\xi^{2})}$	(2.56)
	$\displaystyle=$	$\displaystyle\frac{1}{\gamma}\int\frac{d^{d}k}{(2\pi)^{d}}\int_{0}^{\infty}dt% \ e^{-t({\bf k}+i{\bf x}/2t)^{2}}e^{-r^{2}/4t-t/\xi^{2}}$
	$\displaystyle=$	$\displaystyle\frac{1}{\gamma(4\pi)^{d/2}}\int_{0}^{\infty}dt\ t^{-d/2}e^{-r^{2% }/4t-t/\xi^{2}}$

where, in going to the last line, we’ve simply done the $d$ Gaussian integrals over ${\bf k}$ . At this point there are a number of different routes. We could invoke some specialfunctionology and note that we can massage the integral into the form of a Bessel function

\displaystyle K_{\nu}(z)=\frac{1}{2}\int_{0}^{\infty}dt\ t^{\nu-1}e^{-z(t+1/t)% /2}

whose properties you can find in some dog-eared mathematical methods textbook. However, our interest is only in the behaviour of $G(r)$ in various limits, and for this purpose it will suffice to perform the integral (2.56) using a saddle point. We ignore overall constants, and write the integral as

\displaystyle G(r)\sim\int_{0}^{\infty}dt\ e^{-S(t)}\ \ \ {\rm with}\ \ \ S(t)% =\frac{r^{2}}{4t}+\frac{t}{\xi^{2}}+\frac{d}{2}\log t

The saddle point $t=t_{\star}$ sits at $S^{\prime}(t_{\star})=0$ . We then approximate the integral as

\displaystyle G(r)\sim\int_{0}^{\infty}dt\ e^{-S(t_{\star})+S^{\prime\prime}(t% _{\star})t^{2}/2}=\sqrt{\frac{\pi}{2S^{\prime\prime}(t_{\star})}}\,e^{-S(t_{% \star})}

For us the saddle lies at

\displaystyle S^{\prime}(t_{\star})=0\ \ \ \Rightarrow\ \ \ t_{\star}=\frac{% \xi^{2}}{2}\left(-\frac{d}{2}+\sqrt{\frac{d^{2}}{4}+\frac{r^{2}}{\xi^{2}}}\right)

There are two different limits that we are interested in: $r\gg\xi$ and $r\ll\xi$ . We’ll deal with them in turn:

$r\gg\xi$ : In this regime, we have $t_{\star}\approx r\xi/2$ . And so $S(t_{\star})\approx r/\xi+(d/2)\log(r\xi/2)$ . One can also check that $S^{\prime\prime}(t_{\star})\approx 2/r\xi^{3}$ . The upshot is that the asymptotic form of the integral scales as

\displaystyle G(r)\sim\frac{1}{\xi^{d/2-3/2}}\,\frac{e^{-r/\xi}}{r^{d/2-1/2}}% \ \ \ \ \ r\gg\xi

At large distance scales, the correlation function falls off exponentially.

$r\ll\xi$ : In the other regime, the saddle point lies at $t_{\star}\approx r^{2}/2d$ , giving $S(t_{\star})\approx d+(d/2)\log(r^{2}/2d)$ and $S^{\prime\prime}(t_{\star})\approx 2d^{3}/r^{4}$ . Putting this together, we see that for $r\ll\xi$ , the fall-off is only power law at short distances,

\displaystyle G(r)\sim\frac{1}{r^{d-2}}\ \ \ \ r\ll\xi

We learn that the correlation function changes its form at the distances scale $r\sim\xi$ , with the limiting form

\displaystyle\langle\phi({{\bf x}})\phi({\bf y})\rangle\sim\left\{\begin{array% }[]{cc}\dfrac{1}{r^{d-2}}&r\ll\xi\\ &\\ \dfrac{e^{-r/\xi}}{r^{(d-1)/2}}&r\gg\xi\end{array}\right.

(2.57)

This is known as the Ornstein-Zernicke correlation.

2.2.2 The Correlation Function is a Green’s Function

The result (2.57) is important and we we’ll delve a little deeper into it shortly. But first, it will prove useful to redo the calculation above in real space, rather than Fourier space, to highlight some of the machinery hiding behind our path integral.

To set some foundations, we start with a multi-dimensional integral over $n$ variables. Suppose that ${\bf y}$ is an $n$ -dimensional vector. The simple Gaussian integral now involves an invertible $n\times n$ matrix $G$ ,

\displaystyle\int_{-\infty}^{+\infty}d^{n}y\ e^{-\frac{1}{2}{\bf y}\cdot G^{-1% }{\bf y}}={\rm det}^{1/2}(2\pi G)

This result follows straighforwardly from the single-variable Gaussian integral (2.44), by using a basis that diagonalises $G$ . Similarly, if we introduce an $n$ -dimensional vector ${\bf B}$ , we can complete the square to find

\displaystyle\int_{-\infty}^{+\infty}d^{n}y\ e^{-\frac{1}{2}{\bf y}\cdot G^{-1% }{\bf y}+{\bf B}\cdot{\bf y}}={\rm det}^{1/2}(2\pi G)\,e^{\frac{1}{2}{\bf B}% \cdot G{\bf B}}

(2.58)

Now let’s jump to the infinite dimensional, path integral version of this. Throughout this section, we’ve been working with a quadratic free energy

\displaystyle F[\phi({{\bf x}})]=\int d^{d}x\ \left[\frac{1}{2}\gamma(\nabla% \phi)^{2}+\frac{1}{2}\mu^{2}\phi^{2}({\bf x})+B({\bf x})\phi({{\bf x}})\right]

(2.59)

We can massage this into the form of the exponent in (2.58) by writing

\displaystyle F[\phi({{\bf x}})]=\int d^{d}x\int d^{d}y\ \frac{1}{2}\phi({{\bf x% }})G^{-1}({\bf x},{\bf y})\phi({\bf y})+\int d^{d}x\ B({\bf x})\phi({{\bf x}})

where we’ve introduced the “infinite dimensional matrix”, more commonly known as an operator

\displaystyle G^{-1}({\bf x},{\bf y})=\delta^{d}({\bf x}-{\bf y})\left(-\gamma% \nabla^{2}_{y}+\mu^{2}\right)

(2.60)

Note that this is the operator that appears in the saddle point evaluation of the free energy, as we saw earlier in (1.30).

Given the operator $G^{-1}$ , what is the inverse operator $G({\bf x},{\bf y})$ ? We have another name for the inverse of an operator: it is called a Green’s functions. In the present case, $G({\bf x},{\bf y})$ obeys the equation

\displaystyle(-\gamma\nabla_{x}^{2}+\mu^{2})G({\bf x},{\bf y})=\delta^{d}({\bf x% }-{\bf y})

By translational symmetry, we have $G({\bf x},{\bf y})={G}({\bf x}-{\bf y})$ . You can simply check that the Green’s function is indeed given in Fourier space by our previous result (2.53)

\displaystyle{G}({\bf x})=\int\frac{d^{d}k}{(2\pi)^{d}}\frac{e^{-i{\bf k}\cdot% {\bf x}}}{\gamma k^{2}+\mu^{2}}

This route led us to the same result we had previously. Except we learn something new: the correlation function is the same thing as the Green’s function, $\langle\phi({\bf x})\phi({\bf y})\rangle=\beta^{-1}G({\bf x},{\bf y})$ , and hence solves,

\displaystyle(-\gamma\nabla^{2}+\mu^{2})\,\langle\phi({\bf x})\phi(0)\rangle=% \frac{1}{\beta}\delta^{d}({\bf x})

This is telling us that if we perturb the system at the origin then, for a free energy of the quadratic form (2.59), the correlator $\langle\phi({\bf x})\phi(0)\rangle$ responds by solving the original saddle point equation.

There is one further avatar of the correlation function that is worth mentioning: it is related to the susceptibility. Recall that previously we defined the susceptibility in (1.19) as $\chi={\partial m}/{\partial B}$ . Now, we have a more refined version of susceptibility which knows about the spatial structure,

\displaystyle\chi({\bf x},{\bf y})=\frac{\delta\langle\phi({\bf x})\rangle}{% \delta B({\bf y})}

But, from our discussion above, this is exactly the correlation function $\chi({\bf x},{\bf y})=\beta\langle\phi({\bf x})\phi({\bf y})\rangle$ . We can recover our original, coarse grained susceptibility as

\displaystyle\chi=\int d^{d}x\ \chi({\bf x},0)=\beta\int d^{d}x\ \langle\phi({% \bf x})\phi(0)\rangle

(2.61)

The two point correlation function will play an increasingly important role in later calculations. For this reason it is given its own name: it is called the propagator. Propagators of this kind also arose in the lectures on Quantum Field Theory. In that case, the propagator was defined for a theory in Minkowski space, which led to an ambiguity (of integration contour) and a choice of different propagators: advanced, retarded or Feynman. In the context of Statistical Field Theory, we are working in Euclidean space and there is no such ambiguity.

2.2.3 The Correlation Length

Let’s now look a little more closely at the expression (2.57) for the correlation function which, in two different regimes, scales as

\displaystyle\langle\phi({{\bf x}})\phi({\bf y})\rangle\sim\left\{\begin{array% }[]{cc}\dfrac{1}{r^{d-2}}&r\ll\xi\\ &\\ \dfrac{e^{-r/\xi}}{r^{(d-1)/2}}&r\gg\xi\end{array}\right.

(2.62)

where $r=|{\bf x}-{\bf y}|$ . The exponent contains a length scale, $\xi$ , called the correlation length, defined in terms of the parameters in the free energy as $\xi^{2}=\gamma/\mu^{2}$ .

We see from (2.62) that all correlations die off quickly at distances $r\gg\xi$ . In contrast, for $r\ll\xi$ there is only a much slower, power-law fall-off. In this sense, $\xi$ provides a characteristic length scale for the fluctuations. In a given thermal ensemble, there will be patches where the magnetisation is slightly higher, or slightly lower than the average $\langle m\rangle$ . The size of these patches will be no larger than $\xi$ .

Recall that, close to the critical point, $\mu^{2}\sim|T-T_{c}|$ . This means that as we approach $T=T_{c}$ , the correlation length diverges as

\displaystyle\xi\sim\frac{1}{|T-T_{c}|^{1/2}}

(2.63)

This is telling us that system will undergo fluctuations of arbitrarily large size. This is the essence of a second order phase transition, and as we move forward we will try to better understand these fluctuations.

Numerical Simulations of the Ising Model

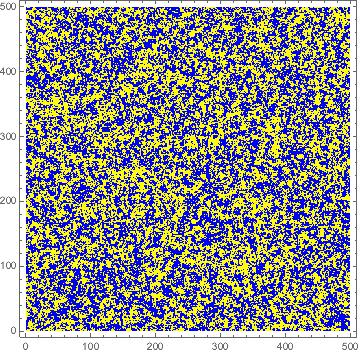
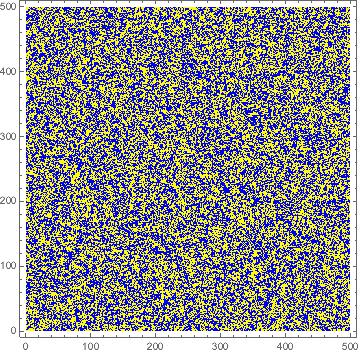
It’s useful to get a sense for what these fluctuations look like. We start in the disordered phase with $T>T_{c}$ . In the figures you can see two typical configurations that contribute to the partition function of the Ising model⁵⁵ 5 These images were generated by the Metropolis algorithm using a mathematica programme created by Daniel Schroeder. It’s well worth playing with to get a feel for what’s going on. Ising simulations, in various formats, can be found on his webpage http://physics.weber.edu/thermal/computer.html.. The up spins are shown in yellow, the down spins in blue.

Spins when — Figure 16: Spins with when $T>T_{c}$

On the left, the temperature is $T_{1}>T_{c}$ , while on the right the temperature is $T_{2}>T_{1}>T_{c}$ . In both pictures, the spins look random. And yet, you can see by eye that there is something different between the two pictures; on the right, when the temperature is higher, the spins are more finely intertwined, with a yellow spin likely to have a blue dot sitting right next to it. Meanwhile, on the left, the randomness is coarser.

What you’re seeing here is the correlation length at work. In each picture, $\xi$ sets the typical length scale of fluctuations. In the right-hand picture, where the temperature is higher, the correlation length is smaller.

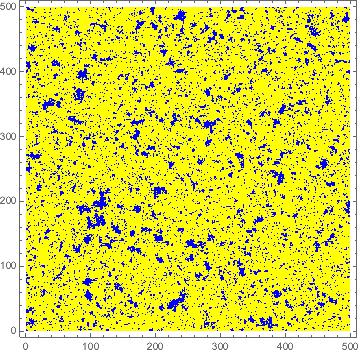
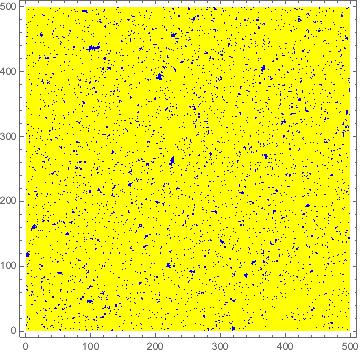
There is a similar story in the ordered phase, with $T<T_{c}$ . Once again, we show two configurations below. Now the system must choose between one of the two ground states; here the choice is that the yellow, up spins are dominant. The left-hand configuration has temperature $T_{1}^{\prime}<T_{c}$ , and the right-hand configuration temperature $T_{2}^{\prime}<T_{1}^{\prime}<T_{c}$ . We see that sizes of the fluctuations around the ordered phase become smaller the further we sit from the critical point.

Figure 20:

T=T_{c}

Finally, we can ask what happens when we sit at the critical point $T=T_{c}$ . A typical configuration is shown in Figure 20. Although it may not be obvious, there is now no characteristic length scale in the picture. Instead, fluctuations occur on all length scales, big and small⁶⁶ 6 The best demonstration that I’ve seen of this scale invariance at the critical point is this Youtube video by Douglas Ashton.. This is the meaning of the diverging correlation length $\xi\rightarrow\infty$ .

Critical Opalescence

There is a nice experimental realisation of these large fluctuations, which can be seen in liquid-gas transitions or mixing transitions between two different fluids. (Both of these lie in the same universality class as the Ising model.) As we approach the second order phase transition, transparent fluids become cloudy, an effect known as critical opalescence⁷⁷ 7 You can see a number of videos showing critical opalescence on Youtube. For example, here.. What’s happening is that the size of the density fluctuations is becoming larger and larger, until they begin to scatter visible light.

More Critical Exponents

We saw in previous sections that we get a number of power-laws at critical points, each of which is related to a critical exponent. The results above give us two further exponents to add to our list. First, we have a correlation length $\xi$ which diverges at the critical point with power (2.63)

\displaystyle\xi\sim\frac{1}{|T-T_{c}|^{\nu}}\ \ \ \ {\rm where}\ \nu=\frac{1}% {2}

Similarly, we know that the correlation function itself is a power law at the critical point, with exponent

\displaystyle\langle\phi({{\bf x}})\phi({\bf y})\rangle\sim\frac{1}{r^{d-2+% \eta}}\ \ \ \ {\rm where}\ \eta=0

Each of these can be thought of as a mean field prediction, in the sense that we are treating the path integral only in quadratic order, which neglects important effects near the critical point. Given our previous discussion, it may not come as a surprise to learn that these critical exponents are correct when $d\geq 4$ . However, they are not correct in lower dimensions. Instead one finds

	MF	$d=2$	$d=3$
$\eta$	$0$	$\frac{1}{4}$	0.0363
$\nu$	$\frac{1}{2}$	$1$	0.6300

This gives us another challenge, one we will rise to in Section 3.

2.2.4 The Upper Critical Dimension

We’re finally in a position to understand why the mean field results hold in high dimensions, but are incorrect in low dimensions. Recall our story so far: when $T<T_{c}$ , the saddle point suggests that

\displaystyle\langle\phi({{\bf x}})\rangle=\pm m_{0}

Meanwhile, there are fluctuations around this mean field value described, at long distances, by the correlation function (2.62). In order to trust our calculations, these fluctuations should be smaller than the background around which they’re fluctuating. In other words, we require $\langle\phi^{2}\rangle\ll\langle\phi\rangle^{2}$ .

It’s straightforward to get an estimate for this. We know that the fluctuations decay after a distance $r\gg\xi$ . We can gain a measure of their importance if we integrate over a ball of radius $\xi$ . We’re then interested in the ratio

\displaystyle R=\dfrac{\int_{0}^{\xi}d^{d}x\ \langle\phi({{\bf x}})\phi(0)% \rangle}{\int_{0}^{\xi}d^{d}x\ m_{0}^{2}}\sim\frac{1}{m_{0}^{2}\,\xi^{d}}\int_% {0}^{\xi}dr\ \frac{r^{d-1}}{r^{d-2}}\sim\frac{\xi^{2-d}}{m_{0}^{2}}

In order to trust mean field theory, we require that this ratio is much less than one. This is the Ginzburg criterion. We can anticipate trouble as we approach a critical point, for here $\xi$ diverges and $m_{0}$ vanishes. According to mean field theory, these two quantities scale as

\displaystyle m_{0}\sim|T-T_{c}|^{1/2}\ \ \ {\rm and}\ \ \ \xi\sim|T-T_{c}|^{-% 1/2}

results which can be found, respectively, in (1.31) and (2.63). This means that the ratio $R$ scales as

\displaystyle R\sim|T-T_{c}|^{(d-4)/2}

We learn that, as we approach the critical point, mean field – which, in this context, means computing small fluctuations around the saddle point – appears trustworthy only if

\displaystyle d\geq d_{c}=4

This is the upper critical dimension for the Ising model. Actually, at the critical dimension $d=4$ there is a logarithmic divergence in $R$ and so we have to treat this case separately; we’ll be more careful about this in the Section 3.

For dimensions $d<4$ , mean field theory predicts its own demise. We’ll see how to make progress in Section 3.

2.3 The Analogy with Quantum Field Theory

There is a very close analogy between the kinds of field theories we’re looking at here, and those that arise in quantum field theory. This analogy is seen most clearly in Feynman’s path integral approach to quantum mechanics⁸⁸ 8 You will see this in next term’s Advanced Quantum Field Theory course.. Correlation functions in both statistical and quantum field theories are captured by partition functions

	Statistical Field Theory:		$\displaystyle\ \ \ Z=\int{\cal D}\phi\ e^{-\beta\int d^{d}x\ {\cal F}(\phi)}$
	Quantum Field Theory:		$\displaystyle\ \ \ Z=\int{\cal D}\phi\ e^{\frac{i}{\hbar}\int d^{d}x\ {\cal L}% (\phi)}$

You don’t need to be a visionary to see the similarities. But there are also some differences: the statistical path integral describes a system in $d$ spatial dimensions, while the quantum path integral describes a system in $d$ spacetime dimensions, or $d-1$ spatial dimensions.

The factor of $i$ in the exponent of the quantum path integral can be traced to the fact that it describes a system evolving in time, and means that it has more subtle convergence properties than its statistical counterpart. In practice, to compute anything in the quantum partition function, one tends to rotate the integration contour and work with Euclidean time,

\displaystyle\tau=it

(2.64)

This is known as a Wick rotation. After this, the quantum and statistical partition functions are mathematically the same kind of objects

\displaystyle Z=\int{\cal D}\phi\ e^{\frac{i}{\hbar}S[\phi]}\ \ \ \rightarrow% \ \ \ Z=\int{\cal D}\phi\ e^{-S_{E}[\phi]/\hbar}

where $S_{E}[\phi]$ is the Euclidean action, and is analogous to the free energy in statistical mechanics. If the original action $S[\phi]$ was Lorentz invariant, then the Euclidean action $S_{E}[\phi]$ will be rotationally invariant. Suddenly, the $d=4$ dimensional field theories, which seemed so unrealistic in the statistical mechanics context, take on a new significance.

By this stage, the only difference between the two theories is the words we drape around them. In statistical mechanics, the path integral captures the thermal fluctuations of the local order parameter, with a strength controlled by the temperature $\beta$ ; in quantum field theory the path integral captures the quantum fluctuations of the field $\phi$ , with a strength controlled by $\hbar$ . This means that many of the techniques we will develop in this course can be translated directly to quantum field theory and high energy physics. Moreover, as we will see in the next section, much of the terminology has its roots in the applications to quantum field theory.

Note that the second order phase transition occurs in our theory when the coefficient of the quadratic term, vanishes: $\mu^{2}=0$ . From the perspective of quantum field theory, a second order phase transition describes massless particles.

Given that the similarities are so striking, one could ask if there are any differences between statistical and quantum field theories. The answer is yes: there are some quantum field theories which, upon Wick rotation, do not have real Euclidean actions. Perhaps the simplest example is Maxwell (or Yang-Mills) theory, with the addition of a “theta term”, proportional to $\epsilon^{\mu\nu\rho\sigma}F_{\mu\nu}F_{\rho\sigma}$ . This gives rise to subtle effects in the quantum theory. However, because it contains a single time derivative, it becomes imaginary in the $\tau$ variable (2.64) and, correspondingly, there is no interpretation of $e^{-S_{E}[\phi]}$ as probabilities in a thermal ensemble.

A Different Perspective on the Lower Critical Dimension

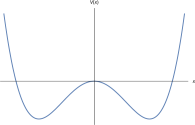
A statistical field theory in $d=1$ spatial dimensions is related to quantum field theory in $d=0$ spatial dimensions. But we have a name for this: we call it quantum mechanics.

Viewed in this way, the lower critical dimension becomes something very familiar. Consider the quartic potential $V(x)$ shown in the figure. Classical considerations suggest that there are two ground states, one for each of the minima. But we know that this is not the way things work in quantum mechanics. Instead, there is a unique ground state in which the wavefunction has support in both minima, but with the expectation value $\langle x\rangle=0$ . Indeed, the domain wall calculation that we described in Section 1.3.3 is the same calculation that one uses to describe quantum tunnelling using the path integral.

Dressed in fancy language, we could say that quantum tunnelling means that the ${\bf Z}_{2}$ symmetry cannot be spontaneously broken in quantum mechanics. This translates to the statement that there are no phase transitions in $d=1$ statistical field theories.