4 Continuous Symmetries
So far we have focussed almost exclusively on the Ising model. Now it is time to diversify. First, however, there is one more lesson to wring from Landau’s approach to phase transitions…
4.1 The Importance of Symmetry
Phases of matter are characterised by symmetry. More precisely, phases of matter are characterised by two symmetry groups. The first, which we will call , is the symmetry enjoyed by the free energy of the system. The second, which we call , is the symmetry of the ground state.
This structure can be seen in the Ising model. When , the free energy has a symmetry. In the high temperature, disordered phase this symmetry is unbroken; here also. In contrast, in the low temperature ordered phase, the symmetry is spontaneously broken as the system must choose one of two ground states; here . The two different phases – ordered and disordered – are characterised by different choices for .
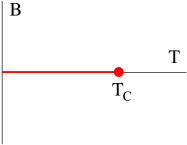
In the ordered phase we have two different ground states, whose phase diagram is reproduced on the next page. Whenever a discrete symmetry group like is spontaneously broken, it results in multiple ground states. One can move from one ground state to another by acting with the broken generators of .
In contrast, when the free energy does not have a symmetry, so . According to Landau’s criterion, this means that there is only a single phase. Indeed, by going to temperatures , it is possible to move from any point in the phase diagram to any other point without passing through a phase transition, so there is no preferred way to carve the phase diagram into different regions. However, this also means that, by varying at low temperatures , we can have a first order phase transition between two states which actually lie in the same phase. This can also be understood on symmetry grounds because the first order transition does not occur at a generic point of the phase diagram, but instead only when is enhanced to .
|
|
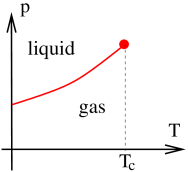
The discussion carries over identically to any system which lies in the Ising universality class, including the liquid-gas system. This leaves us with the slightly disconcerting idea that a liquid and gas actually describe the same phase of matter. As with the Ising model, by taking a path through high pressures and temperatures one can always convert one smoothly into the other, which means that any attempt to label points in the phase diagram as “liquid” or “gas” will necessarily involve a degree of arbitrariness. It is really only possible to unambiguously distinguish a liquid from a gas when we sit on the line of first order phase transitions. Here there is an emergent symmetry, which is spontaneously broken to , and the two states of matter – liquid and gas – are two different ground states of the system. In everyday life, we sit much closer to the line of first order transitions than to the critical point, so feel comfortable extending this definition of “liquid” and “gas” into other regimes of the phase diagram, as shown in the figure.
Beyond Ising
The idea of symmetry, and of broken symmetry, turns out to be useful in characterising nearly all phases of matter. In each case, one should first determine an order parameter and a symmetry group under which it transforms. Sometimes the choice of order parameter is obvious; sometimes it is more subtle. One then writes down the most general Landau-Ginzburg free energy, subject to the requirement that it is invariant under . The different phases of matter within this class are characterised by the group preserved by the ground state.
There are a number of reasons why it is useful to characterise states of matter in terms of their (broken) symmetry. The original idea of Landau was that, as we’ve seen with the Ising model, symmetry provides a powerful mechanism to understand when a phase transition will take place. In particular, there must be a phase transition whenever changes.
However, it turns out that this is not the only thing symmetry is good for. As we will see below, knowledge of and is often sufficient to determine many of the low energy properties of a system, both through a result known as Goldstone’s theorem (that we will describe in Section 4.2) and through various topological considerations (some of which we will see in Section 4.4).
Finally, and particularly pertinent for this course is the role that symmetry plays in the renormalisation group and specifically in universality. One can ask: when do two systems lie in the same universality class? Although the full answer to this question is not yet understood, a fairly good guess is: when they share the same symmetry .
There are many different systems and choices of that we could look at. A particularly interesting class occurs when we take , the group of spatial translations and rotations. The pattern of symmetry breaking provides, for example, a clean distinction between a liquid/gas and a solid, with the latter breaking down to its crystal group. In this framework, there is not one solid phase of matter, but many, with each different crystal structure preserving a different and hence representing a different phase of matter. The different breaking patterns of spatial rotations also allows us to define novel phases of matter, such as liquid crystals. Viewed in this way, even soap, which can undergo a discontinuous change to become slippery, constitutes a new phase of matter. We will not discuss this form of symmetry breaking in this course, but you can learn more about it in next term’s course on Soft Matter.
Here, instead, we will be interested in phases of matter that are characterised by “internal” symmetry groups that are continuous, as opposed to the discrete symmetry of the Ising model. This includes materials like magnets, where the spin is a vector that is free to rotate. It also includes more exotic quantum materials such as Bose-Einstein condensates, superfluids and superconductors. We will see that systems with continuous symmetry groups exhibit a somewhat richer physics than we’ve seen in the Ising model.
Beyond the Landau Classification
The idea that phases of matter can be classified by (broken) symmetries has proven crucial in placing some order on the world around us. However, it is not the last word. Over the past twenty years, it has become increasingly clear that certain highly entangled quantum systems defy a simple characterisation by symmetry. The first, and most prominent, examples are the quantum Hall states. To understand these, one needs a new ingredient: topology. We will not touch upon this here, but you can read more in the lecture notes on the Quantum Hall Effect.
4.2 Models
Phases of matter that are characterised by continuous, as opposed to discrete, symmetries offer a rich array of new physics. The simplest such models contain real scalar fields, which we arrange in a vector
We will ask that the free energy is invariant under the symmetry
where so that . Now, when constructing the free energy we write down only the terms invariant under . The first few are
where rotational invariance requires . These kind of theories are known, not unreasonably, as models. They are of interest for all , but and play particularly prominent roles.
: The XY-Model
When , it is often convenient to pair the two real scalar fields into a single complex field
The free energy now consists of all terms which are invariant under phase rotations, . The first few terms are
| (4.113) |
This is also known as the XY-model or, sometimes, the rotor model.
There are at least two physical systems which sit in this universality class. The first are magnets where, in contrast to the Ising model, each atom has a continuous spin which can rotate in a plane. (This is usually taken to be the plane, which is where the name comes from.) The microscopic Hamiltonian is the generalisation of the Ising model (1.1) to
| (4.114) |
where . This is also written as
where is the angle that the spin makes with some, fixed reference direction. Coarse-graining this microscopic model gives rise to the free energy (4.113). One could also add a magnetic field term , where is also a two-component vector. Such a term would break the symmetry, and introduce terms in (4.113) that are odd in .
The second physical system described by (4.113) is rather different in nature: it is a Bose-Einstein condensate, or its strongly coupled counterpart, a superfluid. Here, the origin of the order parameter is rather more subtle, and is related to off-diagonal long-range order in the one-particle density matrix. In this case, the saddle point of the free-energy leads to the equation of motion
which is known as the Gross-Pitaevskii equation.
It is sometimes, rather lazily, said that can be thought of as the macroscopic wavefunction of the system, and the Gross-Pitaevskii equation is then referred to as a non-linear Schrödinger equation. This is misleading for the simple reason that quantum mechanics is always linear.
: The Heisenberg Model
The case also describes magnets. The microscopic energy again takes the form (4.114), but now where each is free to rotate in three dimensions. This is referred to as the model or, alternatively, as the Heisenberg model.
4.2.1 Goldstone Bosons
The real novelty of continuous symmetries arises in the ordered phase, where and, correspondingly, in the ground state. For the Ising model, we had two possible choices: . The system had to pick one, and in doing so spontaneously broke the symmetry. With a continuous symmetry, we have an infinite number of choices. The minimum of the free energy constrains only the magnitude of which is given by
However, minimising the free energy does not determine the direction of . We are left with a space of ground states which is the sphere . Each point on the sphere, parameterises the direction of and has the same energy. The configuration in which all the spins point like this:
has the same energy as the configuration in which all the spins point like this:
This infinitely degenerate choice of ground states gives us something new. We can consider configurations in which we stay within the space of ground states, but the direction varies in space. For such configurations, the part of the free energy remains minimised, but we pick up contributions from the gradient terms . However, we can always lower this free energy by making the variation take place over longer and longer distances. The upshot is that there are excitations of the system that look like this
which can be made to cost an arbitrarily small amount of energy, by stretching the winding over longer and longer distance scales.
These kind of excitations, which arise from the spontaneous breaking of continuous symmetries, are known as Goldstone bosons, or sometimes Nambu-Goldstone bosons. In the particular context of magnets, they are called spin waves.
There is a dizzying array of names for these kind of excitations, reflecting their ubiquity and importance. In general, an excitation whose energy cost vanishes as the wavelength goes to infinity is referred to as a soft mode or, alternatively, is said to be gapless. These are to be contrasted with gapped excitations whose energy remains finite in this limit. In the context of quantum field theory, “gapless” = “massless”, and “gapped” = ”massive”, with the energy gap coming from .
Gapless excitations often dominate the low-temperature behaviour of a system, where they are the only excitations that are not Boltzmann suppressed. In many systems, these gapless modes arise from the breaking of some symmetry. A particularly important example, that we will not discuss in these lectures, are phonons in a solid. These can be thought of as Goldstone bosons for broken translational symmetry.
The Symmetry Behind Goldstone Bosons
The intuitive idea described above can be placed on more rigorous footing in the form of Goldstone’s theorem. This states that, in any system the spontaneous breaking of a continuous symmetry gives rise to a gapless excitation, the eponymous Goldstone boson. This can be stated in language of group theory.
For our model, the symmetry is broken by a choice of to . (To see this, note that if then there is a surviving symmetry which acts on the on the string of zeros.) The space of ground states has a group theoretic interpretation as the coset space
This idea generalises. If a continuous symmetry is spontaneously broken to , then the manifold of ground states is given by . We get a Goldstone boson for each broken symmetry generator, so the total number is
For the model, and so the number of Goldstone modes is then , which is indeed the dimension of the sphere .
An Example: the XY-Model
It’s simple to write some equations to go with the pictures above. Let’s start with the XY-model. In the ordered phase, we get a so-called Mexican hat potential, as shown in the figure. We can see that there is a circle, of minima. It’s useful to decompose the field as . In the ground state , while is arbitrary. If we write
| (4.115) |
Then the free energy has the expansion
| (4.116) | |||||
Here, the Goldstone boson is . There can be no terms of the form or arising in the free energy. Instead, it has only derivative interactions.
Another Example: The Heisenberg Model
For the model, we decompose the field in spherical polar coordinates,
with and . Once again, in the ordered phase we have , with and arbitrary. Expanding as (4.115), the free energy now takes the form
| (4.117) | |||||
Here and are the two Goldstone modes and, correspondingly, have only derivative interactions. Note, however, that this time the Goldstone modes interact with each other, as seen in the term.
The kinetic terms for the Goldstone bosons above take the form of the metric on the two-sphere , i.e. . This is no coincidence: the Goldstone bosons describe fluctuations around the minima of the free energy . In the present case, this set of minima is , and this geometry gets imprinted on the dynamics of the Goldstone modes. We will explore this more in Section 4.3.
Correlation Functions
We saw in Section 2.2 that the quadratic term in the free energy is related (inversely) to the correlation length . For Goldstone bosons this quadratic term necessarily vanishes and so they have infinite correlation length.
This manifests itself in the correlation function, which decays as a power-law rather than exponential. This is simplest to see in the XY-model. (We will discuss models with in more detail in Section 4.3.) The free energy (4.116) is
where the higher order terms are all derivatives and will not affect the discussion below. To compute the correlation function , we can simply import the result (2.53). (There are some subtleties in doing the path integral because is periodic, now valued in rather than . These subtleties turn out not to be important here but we will revisit them in Section 4.4.) The long distance behaviour is
| (4.118) |
This is similar to the behaviour of the correlation function at the critical point. Indeed, a critical point can be thought of as having gapless excitations. But there are differences.
First, the power-law decay at critical point requires some fine-tuning of a parameter; we must pick the temperature to be exactly . In contrast, spontaneous symmetry breaking is more robust, and we get power-law decay for all . In other words, we have a phase with long range correlations, rather than just a point in the phase diagram. (For , where there is no symmetry breaking, all modes still decay exponentially as in the Ising model.)
The second difference is that Goldstone bosons are much simpler to understand than the gapless modes at a critical point. As we have seen, at critical points the power-law decay of correlation functions suffers a correction due to integrating out short distance modes, resulting in the critical exponent . There are no such subtleties for Goldstone modes since all the dynamics is constrained by symmetry, and the correlation function (4.118). There are two caveats to this statement, both of which we will elaborate upon below. The first is that the simplicity only holds when ; when we sit at the critical point , things become interesting once again. The second caveat is that we have to be above the lower critical dimension for the Goldstone bosons to exist.
4.2.2 The Expansion
At the critical temperature, , the models exhibit critical behaviour. The mean field approach to the model gives the same answer as we saw for the Ising field theory in previous sections. By now, you will not be surprised to learn that these mean field exponents are not always correct. However, the system now does not flow to the Ising critical point. Instead, they lie in a different universality class.
In , the theories flow to a different critical point for each . The critical exponents are known to be:
| MF | 0 | |
|---|---|---|
| Ising | 0.0363 | 0.6300 |
| 0.0385 | 0.6719 | |
| 0.0386 | 0.702 |
where the other critical exponents, , , and all follow from the scaling relations that we saw in Section 3.2.
While the values of and do not look very different from the Ising exponents, there is an important difference in the critical exponent for the heat capacity , which is given by . For both the and transition, is negative. For example, for the transition. This means that the heat capacity exhibits a cusp, rather than a true divergence.
For example, the superfluid transition of helium lies in the XY universality class. The heat capacity has long been known to exhibit cusp-like behaviour as shown in Figure 3499 9 This data is taken from Buckingham and Fairbank, “The Nature of the Lambda Transition”, in Progress in Low Temperature Physics III, 1961.. This characteristic shape means that the second order superfluid transition is sometimes referred to as the “lambda transition”. It turns out that the accuracy in these experiments is limited by the effect of the Earth’s gravitational field. In the 1990s, these measurements were made on a space shuttle flight, in broad (but not perfect) agreement with theoretical prediction of for the critical exponent and suitable coefficients and .
The transition to Bose-Einstein condensate also sits in the XY universality class. This is a particularly clean system which allows precision experiments. For example, the data above shows the behaviour of the correlation length as a gas of ultracold rubidium-87 atoms passes through the critical point. The critical exponent is found to be , in good agreement with the theoretical prediction (albeit with fairly large error bars)1010 10 This data is taken from the paper “Critical behaviour of a trapped interacting Bose gas” by T. Donner et. al., arXiv:0704.1439..
It is not too difficult to repeat the RG calculations that we did in Sections 3.3 - 3.5 for the model. As before, we rescale fields so that our order parameter – which we now call , with – has free energy
The study of the Gaussian fixed point, at , goes through much as before. Indeed, a simple dimensional analysis argument tells us that
and, so
so that is always a relevant deformation, while is relevant in dimensions. So far, nothing depends on .
The differences arise in perturbation theory. The part of the free energy which mixes long and short wavelength modes is
The presence of the internal indices, , means that the interaction has more structure than previously. To reflect this, we need to change our rules for drawing diagrams. First, each line should now be accompanied by an internal index . Second, it is useful to split the interaction vertex as
where the red ellipse splits the four legs into two pairs, each of which is a singlet under the symmetry, as shown in the delta function structure. (You may have to squint in some of the following pictures to see which pairs of legs are contracted.)
Order
We can now run through our previous calculation to see how things change when we have fields. At order , we previously found just a single diagram which renormalised . Now the index structure means that splits into two different contributions. The first is:
The other contribution has a different contraction between internal indices
Note that the overall coefficients are , which agrees with our earlier counting (3.92). Each of these gives the same result we saw for a single scalar field, but with an important difference: the first diagram has an extra factor of , arising from the fact that any of the species can run in the loop. This is general result: any closed dotted loop gives an extra factor of .
Order
A similar thing happens at the next order, with the single diagram at splitting into three different diagrams,
Only the first of these has a closed loop, unattached to the external legs. This comes with a factor of , while the other two do not. A careful computation of the relevant overall factors shows that these diagrams renormalise the quartic coupling as
Again, this reproduces our earlier result (3.104) when .
The Epsilon Expansion
We learn that the general structure of RG flow around the Gaussian fixed point is essentially the same as in the Ising field theory discussed in Section 3; only the coefficients of the beta functions differ. The same structure is also seen in the epsilon expansion. Working in dimension
the beta function equations become, at leading order in and ,
where, as in our earlier discussion, we’ve introduced the dimensionless coupling . The analog of the Wilson-Fisher fixed point sits at
Around this fixed point, the linearised beta functions take the form
where the off-diagonal entry is . This does not affect the eigenvalues which are given by the diagonal entries,
The interacting fixed point has one relevant and one irrelevant direction, just like for the Ising model. To leading order in , the critical exponents are
and
| (4.119) |
Meanwhile is independent of , and the anomalous dimension turns out to be
4.2.3 There Are No Goldstone Bosons in
We learned in Section 1 that field theories have a lower critical dimension, in which the ordered phase ceases to exist. For theories characterised by any discrete symmetry, such as the of the Ising field theory, this lower critical dimension is . As we explained in (1.3.3), the lack of an ordered phase in dimensions can be traced to the existence of domain walls.
The story is different when we have continuous symmetries. Now there are no domain walls because the space of ground states is continuously connected. However, there is a more prominent phenomena which means that the lower critical dimension is raised to .
An Example: the XY model
The lack of ordered phase in dimensions arises due to the presence of the would-be Goldstone modes. This is simplest to explain in the XY model. Let’s sit in the broken phase and focus only on the Goldstone bosons. We must pick a ground state for : this is the essence of spontaneous symmetry breaking. Let’s choose . We now look at fluctuations around this ground state,
| (4.120) |
From the correlation function (4.118), the long distance behaviour is
| (4.121) |
with .
We see that there is a qualitative difference between and . For , the two point correlator decays to a constant as . This constant is cancelled by the other term in (4.120), which means that the phase returns to its original value .
In contrast, for , the fluctuation of the phase grows indefinitely as we go to larger distances. You may have thought that you had placed the system in a fixed ground state, but the thermal fluctuations of the Goldstone mode mean that it doesn’t stay there. The interpretation is that there is no ordered phase with in dimensions or below.
This is a general result, known as the Mermin-Wagner theorem. A continuous symmetry cannot be spontaneously broken in dimensions or below: there are no Goldstone bosons in dimensions.
This leaves us with a delicate question. The existence of the gapless Goldstone modes was predicated on the idea of spontaneous symmetry breaking. But for dimensions, no such symmetry breaking happens. What, then, is the resulting physics?
In , the physics is straightforward: there are no gapless modes. As before, this can also be understood in the language of quantum mechanics, where the spectrum of a particle moving on is discrete and gapped. For , the physics is more interesting. It turns out that the answer is somewhat different for models with and for the XY-model with . We will discuss the fate of the Goldstone modes for each of these in Sections 4.3 and 4.4 respectively.
4.3 Sigma Models
We have still to understand the fate of the Goldstone bosons in dimensions. In this section, we will tell their story. As a spin-off, we will see that we also a get a new handle on the critical point in dimensions.
We place ourselves firmly in the ordered phase, with . Mean field considerations tell us that , leaving us with a space of possible ground states which is identified with the sphere . As we saw in Section 4.2.1, fluctuations in the directions parallel to the have only power-law decay; these are the Goldstone modes. In contrast the “longitudinal” fluctuation, in which , acts very much like in the Ising model and has exponential decay with a correlation length . This suggests that the long distance dynamics is dominated purely by the Goldstone modes.
Here we will study the theory of these Goldstone modes. First, rather than working with , we rescale the field to a new field, which has unit length,
| (4.122) |
For now, we will keep the dimension arbitrary. The free energy is given by
| (4.123) |
where the coefficient is the price that we pay for rescaling to be a unit vector. The free energy (4.123) looks like that of a free theory; all the interactions come from the constraint (4.122) which say that the fields must lie on the unit sphere .
We would like to understand the path integral for the sigma model. Schematically, this can be written as
| (4.124) |
Here we’ve imposed the constraint through a delta function. Note that the only coefficient in the game is ; this will play the role of our coupling constant. Recall that, long ago, before we grew up and set , we used to write the partition function as . Comparing to this form suggests that can be viewed as temperature, with large corresponding to high temperature. This interpretation will be useful later.
We can do some simple dimensional analysis. The field must be dimensionless since it obeys the constraint (4.122). So,
| (4.125) |
In particular, is dimensionless in . Here the theory is weakly coupled when , in the sense that field configurations with wild spatial variations are suppressed in the path integral. Before our rescaling, this corresponds to the case where parameterise a large sphere. In contrast, when these configurations are unsuppressed and the theory is strongly coupled; in this case the parameterise a small sphere.
It is possible to write the sigma model in a more explicit form. We can decompose the vector as
where is an -dimensional vector and is given by
which ensures that the fields sit on the ground state manifold . The free energy is then given by
| (4.126) | |||||
This form of the sigma model does not have any constraint; it is an interacting theory of the Goldstone modes . However, we have paid a price: only an symmetry is now manifest in the free energy, rather than the full symmetry. This is because we have had to make a choice of which of the redundant variables to eliminate in order to solve the constraint (4.122). Related to this, our free energy (4.126) is now only valid as long as anywhere, in which case the second term would diverge. This is because the fields are coordinates on the space and it is impossible to introduce coordinates which are well behaved over the entire manifold.
As an aside: the name “sigma model ” is, obviously, completely uninformative. It has its roots in particle physics where a theory of this type describes the interactions of pions. Strangely, the eponymous “sigma” meson is the one particle not described by the sigma-model; it is analogous to the longitudinal mode which is determined in terms of the fields in our description above.
4.3.1 The Background Field Method
We would like to perform a renormalisation group analysis on the sigma model. There are a number of ways to proceed. First, we could Taylor expand the second term in the free energy for small . This would result in an infinite tower of interactions. We could then restrict attention to the first few, and do the kind of Wilsonian RG treatment we’ve seen before. This method works, but it butchers the underlying geometry and, in doing so, disguises what’s really going on.
Instead, there is a better approach, first introduced in this context by Polyakov, called the background field method. First, suppose that takes some profile which varies slowly in space,
This profile must obey . This will play the role of our long wavelength modes.
On top of this background, we want to introduce short wavelength modes which change rapidly in space. To parameterise these modes, we first introduce frame fields. These are a basis of unit vectors , with and , which are orthogonal to ,
| (4.127) |
The frame fields are, like , slowly varying in space. There is an ambiguity in the definition of these frame fields; we can always rotate them by a local transformation and we will still have a good set of frame fields.
The short wavelength modes sit on top of our original field and fluctuate in the direction of the frame fields. We call these , and write the full configuration as
| (4.128) |
By construction, this configuration still satisfies the constraint (4.122). This is morally equivalent to our previous Fourier space decomposition , but now in real space. We will integrate out the short wavelength modes and determine their effect on the long wavelength mode .
Integrating out Short Wavelengths
We have a short calculation ahead of us. Our plan is to expand the free energy to quadratic order in the short wavelength fields and then integrate them out, in exactly the same way that we integrated out the Fourier modes previously. We will then interpret this in terms of an effective free energy for the long wavelength fields and, in particular, in terms of a renormalisation of the coupling .
First, we have
The gradient term then becomes
where we have used the identities (4.127). One of the cross-terms vanishes by dint of the fact that so that .
Our partition function is now
where the interaction between and are captured in
As previously, we interpret the functional integral over as computing the expectation value of using the probability distribution . In other words,
The expectation value can be Taylor expanded,
| (4.129) |
As usual, the renormalisation group will generate many terms when we integrate out . Our interest is in how the leading order kinetic terms are affected; all other terms will turn out to be irrelevant. At leading order, it is sufficient to focus on . (Given the term linear in , one might wonder if such a term can be generated from ; a closer inspection shows that this in fact gives rise only to terms like .) We have
| (4.130) |
where we’ve used the fact that to lose the linear term. The correlator that we want takes the same form that we calculated in previous sections. (See, for example, (2.54).)
where
Here we’ve introduced the limits on the integral to reflect the fact that, as in our earlier RG analysis, the short wavelength modes – which are here – have support only in . The integral is simple to perform; we have
where is the area of the unit sphere . Substituting this into (4.130), it is clear that the first term corrects the kinetic term in the sigma model. But what of the second term? Using the fact that the correlator is proportional to , it takes the form . We can massage this into the form we need using some identities. Between then, the fields provide an orthonormal basis of . Inverting this, we have
| (4.131) |
Using this, we can write
But since , we have so
where, in going to the second line, we’ve used (4.131) again, together with the fact that . The first term is just what we want; the second term is a new term that we can add to the sigma model and will be generated by RG. It is related to the geometric concept of torsion; it turns out to be irrelevant and we will not discuss it further here.
Both terms in (4.130) now give a contribution to ; the first is ; the second is simply . The upshot of this is that the includes the term
We now exponentiate this so that, to the order we’re working at, (4.129) becomes . This gives us an effective free energy for the long wavelength field ,
with
Usually there are two further steps in the RG programme. First, we need to rescale our momentum cut-off back up to , and in doing so rescale all length by . This proceeds as before. The second step, advertised in Section 3, is to rescale the fields so that the kinetic term is canonically normalised. This step is not for us, since the normalisation of the kinetic term is the only coupling we have. Instead, the fields are normalised correctly by imposing the constraint (4.122). The upshot is that we have the running coupling constant
| (4.132) |
The first term comes from the naive dimensional analysis that we saw in (4.125); the second term is the one-loop correction from integrating out the high momentum modes.
Note that this second term vanishes when . This reflects the fact that the Goldstone boson in the XY-model is free; this can be seen in (4.116) where there are no interaction terms. Interesting things happen in the XY-model but we will postpone discussion to Section 4.4. In contrast, for the Goldstone bosons are interacting, as can be seen for the model in (4.117), and this drives the running of the coupling constant.
4.3.2 Asymptotic Freedom and the Expansion
Let’s look more closely at the running coupling (4.132). To start, consider what happens in dimensions. As previously, we write
and compute the beta function
The beta function vanishes for . This is because, as we mentioned above, the Goldstone mode in the XY model is non-interacting. However, for the beta function is positive. It means that is an example of a marginally relevant coupling: as we flow the infra-red, gets larger and the theory becomes strongly coupled. Correspondingly, the theory is weakly coupled in the ultra-violet. This property is known as asymptotic freedom, which refers to the fact that the theory is free at asymptotically high energies.
Asymptotically free theories are rather rare in physics. Perhaps the best known example is QCD or, in general, Yang-Mills theory with some small number of matter fields.
The sign of the beta function is telling us that, in (and indeed in ), the weakly coupled ordered phase that we started with is unstable. This is a manifestation of the Mermin-Wagner theorem that we mentioned in Section 4.2.3; there are no Goldstone bosons in . Unfortunately to really understand the infra-red physics in these low dimensions we will have to figure out how to deal with the strongly interacting theory. We will introduce a particularly useful approach in Section 4.3.3.
In higher dimensions, say , the beta function is negative. This means that the sigma-model flows towards weak coupling in the infra-red, telling us that the ordered phase is stable.
However, there is now something new we can do. We can look at what happens in dimension
Here the beta function takes the form
This has a fixed point that lies within the remit of perturbation theory, namely
| (4.133) |
However, in contrast to the story of Section 4.2, this is now a UV fixed-point, rather than an IR fixed point. How should we interpret this?
To understand this, let’s recap the story so far. The model, with unconstrained fields , has a Wilson-Fisher fixed point in dimension . This has one relevant deformation which is, roughly speaking, . If we turn on this relevant deformation with negative sign, we flow to the ordered phase which is described by our sigma model.
What we’ve seen above is this story in reverse. Starting from the ordered phase, described by the sigma model, we have managed to claw our way back up the RG flow to find a UV fixed point, at least in dimensions . It is natural to identify this with the Wilson-Fisher point, viewed through different eyes. This provides us with a different handle on the Wilson-Fisher fixed points for ; we can either approach them from above using the expansion, or from below using the expansion.
To extract the critical exponent , we need to understand how is related to the temperature. From our definition of the path integral (4.124), we see that sits in the exponent where would sit in a usual partition function. This motivates us to identify with temperature and the fixed point with the critical temperature . We then linearise about the fixed point by writing to find
This gives and, correspondingly, the critical exponent
| (4.134) |
independent of . To compute the critical exponent , one could add the interaction or, alternatively, extract the anomalous dimension of from the calculation above. One finds that
The expansion does not give great results if we just go ahead and plug in . But then, there is little reason that it should! For example, for , we can compare the best known results with mean field, and with the and expansions, where we work to first order and plug in . We have
| MF | 0 | |
|---|---|---|
| 0 | 0.61 | |
| 1 | 1 | |
| Actual | 0.0386 | 0.702 |
Nonetheless, there is some utility in having two expansion parameters, coming from different ends. By going to higher powers in , one can try to use sophisticated matching techniques to join together the two expansions and get a better handle on the values of the critical exponents for .
4.3.3 Large
So far, we have seen that the dynamics of interacting Goldstone modes (i.e. ) becomes strongly coupled in dimensions. But we have yet to figure out what actually happens.
Questions like this are typically hard. As , it naively appears that all field configurations contribute equally to the path integral, no matter how wildly they vary and how far they are from the saddle point. We have very few techniques to deal with such situations. Often we have to turn to some hidden and surprising symmetry, or to some unusual limit where the theory is soluble.
In the present case, it turns out that such a limit exists: it is . To proceed, we first rewrite the delta-function in the path integral (4.124) as
| (4.135) | |||||
Here the field plays the role of a Lagrange multiplier; integrating it out gives us back the delta-function, imposing the field constraint .
Now, however, we’re left with a free energy which is quadratic in the . Instead of integrating out , we can instead integrate out . This gives us
Here the determinant of the differential operator should be viewed, in the usual way, as the product of all its eigenvalues, with a truncation associated to the UV cut-off , reflecting the fact that the eigenfunctions can’t oscillate at high frequencies. This determinant will, in general, be a complicated function of , and it does not look as if we are any closer to evaluating the path integral. We can, however, use the standard “” identity to write the partition function as
| (4.136) |
The factor of in front of the first term is what gives us hope because, in the limit , this term is then crying out to be evaluated by saddle point. However, we’re still left with the second term. We can only apply the saddle point technique to this too if we scale the coupling with in a particular way. Specifically, we send , keeping fixed.
The path integral (4.136) is then dominated by the minimum. We use the identity , to find that the saddle point is
| (4.137) |
where is the Green’s function for the operator . This equation looks somewhat foreboding, but is rather simple in Fourier space. First, we look for constant solutions, of the form
Note the factor of ; our saddle point sits on the complex plane, but is nonetheless still applicable. The saddle point (4.137) then becomes simpler in Fourier space: we have
| (4.138) |
where we’ve explicitly included the UV cut-off in the integral. This equation should now be viewed as an equation for .
Large in
It is perhaps no surprise by now to learn that solutions to (4.138) depend on the dimension . Our main concern was with the fate of the Goldstone bosons in . Here the integral gives us
| (4.139) |
If we start with a weakly coupled theory in the UV, , then we can self-consistently assume that to find the solution
| (4.140) |
This simple formula is interesting for several reasons. First, let’s understand the physical interpretation of setting . Referring back to (4.135), we see that it induces an effective quadratic term for in the free energy. This kind of term was supposed to be prohibited by Goldstone’s theorem, but here we see that it is generated – at least in the large limit – by thermal fluctuations in dimensions. This means that the Goldstone bosons in are no longer gapless. Correspondingly, if we compute their correlator using (4.135), we will see that it decays exponentially, with a finite correlation length given by .
The second interesting fact about (4.140) is that the dynamically generated scale is exponentially smaller than the UV cut-off . Indeed, the function has the lovely property that its Taylor expansion around vanishes at every order in . This means that the gap will not show up in any order in perturbation theory in . We say that it is a non-perturbative effect.
Although the calculation we presented above is valid for , it turns out that the conclusions hold for all ; that is, for any theory of interacting Goldstone bosons in dimensions. This means that there is no phase transition for models with in dimensions. As we lower the temperature, mean field theory suggests that we enter an ordered phase with gapless excitations, but this is misleading: instead, thermal fluctuations destroy both the order and gapless modes.
The discussion above carries over directly to quantum field theory, where non-linear sigma models in dimensions are also of great interest. Here the interpretation of the calculation is that the Goldstone modes – which appear to be massless in the classical action – get a mass due to quantum effects. If one didn’t think carefully about the meaning of quantum field theory this appears miraculous because the sigma-model in dimensions has only a dimensionless coupling . Yet somehow, the theory generates a mass out of this dimensionless coupling, a phenomenon that is known as dimensional transmutation. The reason that this is mathematically possible is because a quantum field theory, like is statistical counterpart, is not defined by the classical action (or free energy) alone. It also requires a UV cut-off . And, as we see in (4.140), it is this UV cut-off which provides the dimensional scale for the mass.
Finally, I should mention that if you can do a calculation like the one above for Yang-Mills in dimensions (or, indeed, in dimensions) then fame and fortune awaits. The massless gauge bosons that appear in the classical action are strongly believed to get a mass through quantum effects, yet this remains to be proven. This is the famous “Yang-Mills mass gap” problem. The sigma model in dimensions provides a useful analogy for how this might happen.
Large in
We can also ask if our large analysis can shed any light on the Wilson-Fisher fixed point in . (Or, if you’re willing for dimensions to wander, in .) Here we find something interesting. The saddle point equation (4.138) has different behaviour for and for ,
| (4.141) |
where we haven’t been careful about the coefficients in front of either term, except to stress that the second term comes with a negative sign relative to the first. (We also analysed the behaviour of this integral in (2.46), but there only kept the leading term.) This equation now has rather different behaviour than the corresponding equation (4.139) in . In particular, when the theory is weakly coupled at the cut-off scale, in the sense that
there are no solutions to (4.141) for . In this case, one finds that the saddle point of the free energy actually arises when gets an expectation value. In other words, it’s reconfirming our expectation that the low-energy physics is that of Goldstone bosons.
In contrast, as the theory becomes more strongly coupled at the cut-off scale, there is a critical value
at which solutions to (4.141) for start to appear.
As in the previous section, we identify the deviation from with the temperature,
We can then ask how the correlation length diverges as we approach this critical coupling from above. Here the story is different for and , because of the different behaviour of the subleading term in (4.141). For , we have
which gives the critical exponent
Rather wonderfully, this agrees precisely (for all ) with the result of our expansion (4.134), and with the large limit of our result from the expansion (4.119). Indeed, this result is exact in the limit and can be used as the starting point for a expansion
Meanwhile, when we can read off the behaviour from (4.141); we have
This, of course, is the mean field value that we expect.
4.4 The Kosterlitz-Thouless Transition
The Mermin-Wagner theorem means that any system with a continuous symmetry has no ordered phase in dimensions. As we saw in the previous sections, for the model with , the would-be Goldstone modes are interacting and become gapped as a result of the thermal fluctuations. This means that these models do not exhibit a phase transition as the temperature is lowered.
However, the results of the previous section do not hold for the XY model with . In this case, the sigma-model coupling does not run, and the system remains gapless at low temperatures. As we will now see, the resulting physics is rather more subtle and interesting.
The first surprise is that the XY model does exhibit a phase transition as the temperature is lowered. However, it is somewhat different from the kind of phase transitions that we have met so far. In particular, as we saw in Section 4.2.3, thermal fluctuations mean that there can be no spontaneous breaking of continuous symmetry in and, correspondingly, there is no local order parameter that distinguishes the two phases. Instead, that task falls on the correlation function.
In the high temperature phase, we work with the complex field . The free energy has a quadratic term and, as we’ve now seen many times (starting in (2.62)) the correlation function decays exponentially
| (4.142) |
with . In contrast, in the low temperature phase we have and, as we described in Section 4.2, we can write , with the long distance physics dominated by . To leading order, we can write the free energy as
| (4.143) |
Very low temperatures correspond to .
The correlation function for this Goldstone mode exhibits a log divergence (4.121),
To compare to (4.142), we should look at
where the final equality follows because we are dealing with a Gaussian theory (4.143) and so can employ Wick’s identity (3.98). We learn that, in the low temperature phase, the correlation function for the XY model takes power-law form
| (4.144) |
where the anomalous dimension is given by
Note that this power-law does not occur just at a critical point, but for a range of temperatures. As we increase the coupling , which is equivalent to increasing the temperature, the anomalous dimension increases. We see that the coupling in the XY model (which can be traced to the coupling in the original theory) is something rather rare: it is an example of a genuinely marginal coupling.
The correlation function exhibits two different behaviours in the high temperature (4.142) and low temperature phases (4.144). This suggests that there may be a phase transitions between them. The fact that the order parameter for this phase transition is non-local – it involves the position of fields at two distinct points rather than one – is our first hint that this phase transition has a slightly different smell from others. As we will now see, this is not the only thing that sets it apart.
4.4.1 Vortices
The mechanism for the phase transition can be found within the sigma model approach (4.143), but involves something a little novel. The novelty arises from the fact that, in contrast to the Ising field that we worked with in Section 3, the field is periodic. There can be field configurations, localised around a point , in which winds some number of times,
Crucially the winding number must be an integer so that comes back to itself up to a shift. A configuration with is referred to as a vortex; when , it is an anti-vortex. These are examples of topological defects. The configurations of lattice spins that correspond to a vortex and anti-vortex are shown in the figures.
At the location of the vortex, the field is not well defined. One way to proceed is to revert to the original XY model and allow the magnitude of to vary close to the core. However, for our purposes it will suffice to do something simpler: we just admit ignorance on short distance scales, and say that the vortex has some core size which we denote as . This will later play the role of the UV cut-off in our system.

|

|
We’ll start by giving a rough and ready derivation of the effect of vortices. A configuration with winding has , and so free energy
| (4.145) |
where, in addition to the UV cut-off , we also need to place the system in a finite size to avoid a long-distance divergence in the energy. We’ve also included a contribution from the vortex core region which depends on the microscopic details. Note that the free energy of multi-vortices, with , scales as and so is energetically disfavoured. For this reason we focus on configurations with .
The logic now is very similar to the story of domain walls in dimension that we met in Section 1.3.3. The probability of a vortex configuration arising in the system is enhanced by the fact that it can sit anywhere; this gives an extra factor of . We then have
We see that, when surpasses a critical value,
| (4.146) |
then there is no suppression of vortices; their entropy, coming from the fact that they can sit anywhere on the plane, wins out over their energetic cost. As in the previous section, can be viewed as the temperature of the system, and translates into a temperature scale , above which vortices proliferate. This, it turns out, is responsible for the change in the behaviour of the correlation function, with the vortices randomising the phase , destroying the delicate power-law fall off (4.144).
This phase transition, driven by proliferation of vortices, is known as the Kosterlitz-Thouless transition, and is important both for superfluid films, and for the melting of two-dimensional lattices, where the defects play the role of vortices. It is also known as the BKT transition, as the Russian theorist Berezinskii was the first to appreciate that such a transition is possible, although he didn’t fill in all the details. It is sometimes referred to as a topological phase transition, because it is driven by the proliferation of topological defects.
Michael Kosterlitz and David Thouless are both Brits, educated in Cambridge, who subsequently moved to the US. In fact, Thouless was the first Director of Studies of physics in Churchill College. They shared the 2016 Nobel prize in physics for their work on this transition.
A Coulomb Gas of Vortices
The quick discussion above shows that vortices proliferate when gets too large. But we can do better. The first step is to appreciate that what really emerges as we increase the coupling is a gas of vortices and anti-vortices. The Kosterlitz-Thouless transition is better thought of as an unbinding of vortex-anti-vortex pairs.
To see this in more detail, we will first look at the interactions between vortices. To this end, it’s useful to think in terms of the vector field
| (4.147) |
In the context of superfluids, this is the velocity field. The equation of motion for is
| (4.148) |
A smooth vector field defined by (4.147) would obey . However, in the presence of vortices, the field admits singularities and, correspondingly, the velocity field obeys
| (4.149) |
where is the unit vector out of the plane, and determines the charge of the vortex at position .
We can perform a change of variables to transform (4.148) and (4.149) into more familiar equations. We define
and the equations of motion then become
| (4.150) |
These are the Maxwell equations for the auxiliary electric field , with the vortices acting as “electric charge”. This means that we can import our machinery from our course on Electromagnetism; the only difference is that our electric field lives in spatial dimensions. For example, to determine the interaction between two vortices, we need to solve the Gauss’ law equation in (4.150). We do this by writing , where
| (4.151) |
The free energy (4.143) can be expressed in terms of the electric field as
This looks very similar to our starting point (4.143), except that the relationship between the original field and the new field is given by , which is not straightforward to solve. However, it is now straightforward to compute the free energy. First integrating by parts, we have
where, to get the second equality, we’ve substituted in the expressions (4.150) and (4.151) and, for the cases , replaced our expression with the energy of the core of the vortex. We learn that the interaction between vortices grows logarithmically. This is the Coulomb force in dimensions; it is repulsive for vortex pairs, and attractive for a vortex-anti-vortex pair.
We can now use this expression to write down an expression for the partition function of the XY sigma model. There are two contributions. To isolate these, we decompose the velocity field as
The first of these obeys
This is circulation-free flow in the absence of vortices. It describes the contribution from the fluctuations of : we call these “spin waves”. The second contribution comes from vortices and obeys . The free energy, and hence the partition function, then factorise into two
The spin wave piece is harmless; it shows no sign of a phase transition. Meanwhile, the vortex piece contains contributions from all number of vortices and anti-vortices. We restrict attention to configurations that have equal number of vortices and anti-vortices, as these don’t suffer the IR divergence (4.145) in their free energy. We’re left with
| (4.152) |
where the initial comes from the configuration with no vortices, and the can be thought of as the fugacity of vortices. Here denote the positions of vortices, and the positions of anti-vortices. Meanwhile, the argument of the logarithm involves the sum over the separations , of all (anti)-vortices, regardless of their charge. Finally, the integral should be taken over all so that the cores of vortices do not overlap.
is the partition function of a neutral Coulomb gas in the grand canonical ensemble, with the charges interacting through the 2d Coulomb force.
We would like to understand the phase structure of as the coupling is varied. There are different ways to go about this. One possibility is to implement the RG directly on . This proceeds by integrating out the vortices that are separated on by some short distance scale , effectively increasing the UV cut-off scale . Here we will take an alternative approach. We will first map the Coulomb gas to a seemingly very different problem, one which will be more amenable to the traditional RG methods that we’ve been using in this course.
4.4.2 From Coulomb Gas to Sine-Gordon
The Coulomb gas (4.152) lies in the same universality class as the so-called Sine-Gordon model. This is a theory of a real scalar field , with free energy,
| (4.153) |
The name is a physicist’s version of a joke: it is a play on ‘‘Klein-Gordon” theory1111 11 Sidney Coleman has a famous paper on this model which starts with the sentence “The Sine-Gordon equation is the sophomoric but unfortunately standard name for…”..
We start by giving a quick derivation of the equivalence between the Sine-Gordon model and the Coulomb gas. We will be fairly heuristic. It turns out that this mapping is somewhat simpler if we revert back to a spatial lattice, rather than working in the continuum.
To this end, we introduce a lattice with spacing with lattice sites . On each lattice site, we include a variable which can take values . The interpretation is that if , there is a vortex at this site; if there is an anti-vortex; and if the site is empty. We allow to only take these three values to reflect the fact that two vortices feel a large repulsion, which means that they effectively have a hard core, while a vortex and an anti-vortex annihilate to nothing if they come too close.
The grand canonical partition function (4.152) can then be rewritten as
| (4.154) |
We restrict the sum to configurations that are neutral, so . This mimics the sum over all numbers and positions of vortex-anti-vortex pairs.
To proceed, we will use the fact that the log that appears in is the Green’s function for the 2d Laplacian . In general, we have
where we’ve dropped a factor of the determinant which gives an unimportant overall contribution to the partition function. Using this, the partition function (4.154) can be rewritten yet again as
where we’re using a slightly unholy mix of continuous notation and discrete notation. You should think of as the value of at the lattice site, and write your preferred discretised version of the kinetic term. Now we can do the sum over the ; we have
This is the Sine-Gordon model, as promised. Although our derivation used an underlying lattice, the final result is expressed as a continuum field theory, and this is the form we will use moving forward. As always, however, the memory of the lattice will remain in the UV cut-off scale . The dictionary between the couplings in (4.153) and those of the original XY-model are
We will now see how these couplings fare under the renormalisation group.
4.4.3 RG Flows in Sine-Gordon
We apply our standard RG programme to the Sine-Gordon model,
where we’ve added the subscript to reflect that fact that this free energy is defined at the cut-off scale .
What follows next is familiar. We work in Fourier space and decompose the field into low and high momentum modes,
where includes all modes in the momentum shell . We also define and in real space as the inverse Fourier transform of and respectively.
We then integrate out the high momentum modes to leave ourselves with an effective free energy,
| (4.155) |
where
and the expectation value reflects the fact that we’re integrating out the fast momentum modes, weighted with
Our goal is to compute this effective free energy.
First Order in
We will assume that is suitably small, so that leading order term is
Meanwhile, we can use our handy Wick identity (3.98) to write
The propagator for the fast mode, evaluated at the same point, is
| (4.156) |
The upshot of this calculation is that the interaction term is renormalised after integrating out the high momentum modes, and becomes
and the coupling becomes
The next step of the RG is the rescaling, . It’s simple to check that the rescaling of the field is trivial. With this, our free energy becomes
with
| (4.157) |
Already we can see the essence of the Kosterlitz-Thouless phase transition in this equation. When is suitably large,
then the effect of RG is to reduce . This means that the coupling is an irrelevant operator and, as we flow towards the infra-red, . In this case, the free energy for is given just by the gradient terms, and the correlation function will exhibit a power-law fall off.
In contrast, when is small,
the operator becomes relevant, growing as we go towards the infra-red1212 12 This same result is derived in a very different way, using conformal field theory, in the lectures on String Theory. It can be found in Claim 2 of Section 4.3.3 where, in the notation of that course, the operator is shown to have dimension . A quick check of the conventions for the propagator shows that we should set so that and the operator is relevant if .. Now the minimum of the potential is at mod . Expanding the potential about this minimum gives a quadratic term for and correlation functions will now be exponentially suppressed, with a finite correlation length. It is perhaps surprising that our sophisticated RG analysis gives exactly the same value for the critical coupling as our previous, hand-waving discussion of vortex proliferation (4.146).
Using our earlier result (4.144) for the anomalous dimension, we see that at the phase transition, , the system exhibits a universal anomalous dimension,
Second Order in
At order , we find ourselves with the double cosine
where, as a space-saving measure, I’ve put the spatial position as a subscript, . Taking the logarithm in (4.155) means that we subtract the disconnected diagrams, . The upshot is that, at order , the effective free energy includes the piece
The expectation values that sit in the exponents are given by
Previously we needed only ; now we see that the correlator at spatially separated points also arises. We have
At first sight, we seem to have a non-local free energy involving a double integral. To massage it into something more familiar, we need to realise that the function receives contributions from a small sliver of Fourier modes, and so decays quickly at distances . This means that the functions are non-zero only in a small window .
We write and Taylor expand the factors in the integral for small . For the first, we have simply
The second is more interesting for us; we have
Our free energy, at order , then becomes
| (4.158) |
where all the messy details have been absorbed into two functions
| (4.159) |
We see that the RG flow has generated two terms for us in (4.158). The first, , is something new: it can be viewed as the effect of two vortices, which we didn’t include in our original Sine-Gordon model but is generated upon integrating out high momentum modes. We will not need this here. The second term is something familiar: it is renormalisation of our kinetic term. The final steps of the RG procedure tell us to rescale space, , but also rescale the field so that the kinetic term remains canonically normalised, as in (3.70). We have
This rescaling gets spat out inside the potential, where it has the effect of renormalising our other coupling, . We have
| (4.160) |
Recall that, in terms of our original XY model, . Looking back to our XY sigma model (4.143), we see that it renormalises the coefficient of the kinetic term. This is sometimes called the spin wave“stiffness”, since it measures how difficult it is to twist the spins. The intuition behind the result (4.160) is that a gas of vortex-anti-vortex pairs screens the spins, reducing their stiffness.
Beta Functions
Our task now is to understand the global properties of the resulting RG flow. We write down the beta function in terms of . From (4.157) we have
Meanwhile, from (4.160), we get
where is a positive function that we could extract from the formula (4.159); it’s exact value will not be important for us. Written in terms of , this latter RG equation becomes

|

|
The global structure of the RG flow is shown in the figure. To get a sense for this, first note that if is small, and , then will be rapidly driven to zero; this is the low-temperature phase in which correlation functions drop off with a power-law. Meanwhile if then will be pushed large. This is the high temperature phase, with a non-vanishing correlation length. In the high temperature phase, we see that as . Meanwhile, in the low temperature phase is finite as . At the transition, there is a jump
To see the larger picture, it’s best to zoom in to the phase transition itself. We define
For and small, the beta functions become
From this we can compute
In other words, close to the critical point, the flows are hyperbolae. A general flow can be written as
where are the initial “bare” values of the couplings at the cut-off scale. There are two regions with ; these correspond to the low and high temperature regimes that we discussed above. The separatrix at is given by . The line with flows directly to the critical point. The line with flows away from the critical point.
Suppose that we start on the left of the figure, with . Then the initial data, shown as a dotted line in the figure, is . As we vary this data, we pass through the phase transition. In this sense, it is natural to think of this initial data as a function of the temperature , with
ensuring that we hit the critical point when .
Finally, we can ask about the correlation length . To compute this, we can look at flows with which don’t quite hit the axis. We have
which we can solve to give
This has the slightly odd property that as remains finite. This is an artefact of our approximation but, nonetheless, can be used to our advantage. By the time , we also have and the theory is in the gapped phase. We can stop the RG flow here and use this as a proxy for our correlation length which, as we approach the phase transition from above, scales as
We’re are used to a fairly soft divergence in the correlation length as we approach the critical temperature. For the Kosterlitz-Thouless transition, the change is much more dramatic. This also has an effect on the thermodynamic free energy which, as an extensive quantity scales as . As we approach the phase transition from above, we have
This is a very weak singularity. There is no discontinuity in the heat capacity. Moreover, there is no discontinuity in any derivative of the free energy. In terms of Ehrenfest’s original classification, the Kosterlitz-Thouless transition is rather strange: it is a phase transition of infinite order.