| Department of Applied Mathematics and Theoretical Physics |

Natalia G BerloffProfessor of Applied MathematicsFellow of Jesus CollegeResearch interests: Quantum hydrodynamics and physics-inspired computing understanding and exploiting coherence in non-equilibrium quantum systems: Bose Condensation of excitons and polaritons, magnons, atomic gases, superfluid helium, strong light-matter coupling in solid-state systems, quantum simlators, physics-inspired and physics-based computing.
Several platforms are currently being explored for simulating physical systems whose complexity increases faster than polynomially with the number of particles or degrees of freedom in the system. Many of these computationally intractable problems can be mapped into classical spin models such as the Ising and the XY models and be simulated by a suitable physical system. My research investigates the use of physical systems with analog minimization capabilities. Such systems function with continuous variables and present a viable approach for tackling discrete combinatorial challenges. This includes quadratic binary minimization, a notable issue in the classical Ising minimization of discrete spins, where both theoretical proposals and experimental realizations of physics-based analog systems have been explored. More details of our research on physics-inspired computing can be found at π-Computing Research group website. We are part of the HeInsingberg EU Pathfinder project
HeIsingberg Project
entitled "Spatial Quantum Optical Annealer".
One direction of my research is to relate and improve different mathematical models of superfluid turbulence by developing hierarchies of new stochastic models of vortex motion and turbulence. Mathematical models of superfluidity and superfluid turbulence have used four approaches: (1) the phenomenological Landau two-fluid model, (2) the phenomenological Hall-Vinen-Bekherevich-Khalatnikov (HVBK) model, (3) classical inviscid model of vortex motion with ad hoc reconnections, and (4) the Gross-Pitaevskii (GP) semi-classical model. The first of these was designed to describe the superfluid motion at all temperatures at which superfluidity exists. It requires modification when the vorticity is present. The HVBK model is intended for situations in which superfluid lines are dense. The GP model is applicable at very low temperatures where normal fluid is absent; it has proved its worth especially recently in describing dilute condensates. (Image at right adapted from N.G.Berloff and B.V. Svistunov, Phys. Rev. A, 66 , 013603, 2002.) 
The aim of my research on superfluid turbulence is to model and investigate the fundamental processes of superfluid turbulence in Bose-Einstein condensates (BEC). The central idea is to develop a hierarchy of new models of vortex motion in which the action of sound waves on the large-scale superfluid motion is parametrised in terms of simple random dynamic forces representing sound acting on nonlinear `reduced' dynamic equations with relatively few degrees of freedom representing the vortex motion. Spatially inhomogeneous parameters of the random forcing will be estimated from the statistics diagnosed from the Gross-Pitaevskii (GP) equation. There are three major tasks to achieve this goal: (A) To use GP theory to study the reconnection process in order to evaluate quantitatively the associated radiation of sound and Kelvin waves and to define the reconnection rules for the vortex dynamics; (B) To develop a new method of decomposing the superfluid turbulence into the time-dependent large-scale vortex motion and sound components which makes transparent the sound/sound and vortex/sound nonlinear interactions and allows us to understand the fundamental dynamics involved; (C) To repeat (A) and (B) for nonlocal and dissipative GP models that have different acoustic properties. Finally, there is a hope that the random-forcing parameters can be expressed in terms of the large-scale flow characteristics -- this would be a new turbulent closure. (Image at left: cover page of PRL featuring N. G. Berloff and C. F. Barenghi, Phys. Rev. Lett. 93, 090401, 2004 )
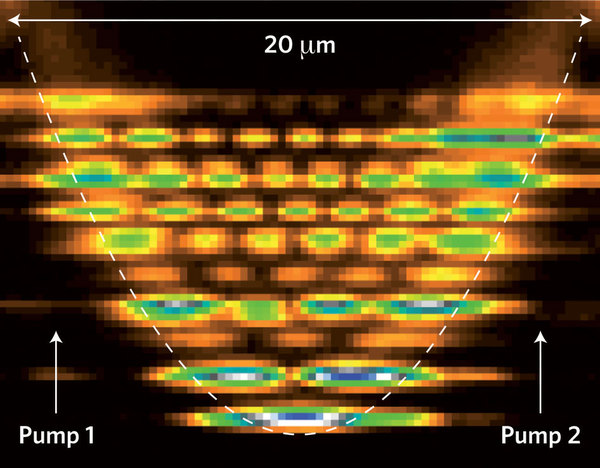
A separate line of investigation focuses on exciton-polariton condensates. Microcavity exciton-polaritons are quasi-particles that result from the hybridisation of excitons and photons confined inside semiconductor microcavities. At low enough densities, they behave as bosons according to Bose-Einstein statistics, and so one may investigate Bose-Einstein condensation of these quasi-particles. Because of the imperfect confinement of the photon component, exciton-polaritons have a finite lifetime, and have to be continuously re-populated. Therefore, exciton-polariton condensates lie somewhere between equilibrium Bose-Einstein condensates and lasers. Similar to other laser systems nonequlibrium nature of the polariton condensates gives rise to different kinds of interesting pattern formation. Specific to polariton condensates, the mechanism responsible for pattern formation is an intricate interplay between nonlinear interactions, forcing, dissipation, dispersion and intrincic disorder in the material. The key to understanding the universal behaviour of pattern-forming systems lies in a common description obtained when particular microscopic models reduced to an order parameter equation. This project concerns with development of such models in close interaction with experimental groups such as Nanophotonics group of Professor Jeremy Baumberg (Cavendish). (Image at right adapted from G. Tosi et al Nature Physics, 8, 190-194 2012 ) 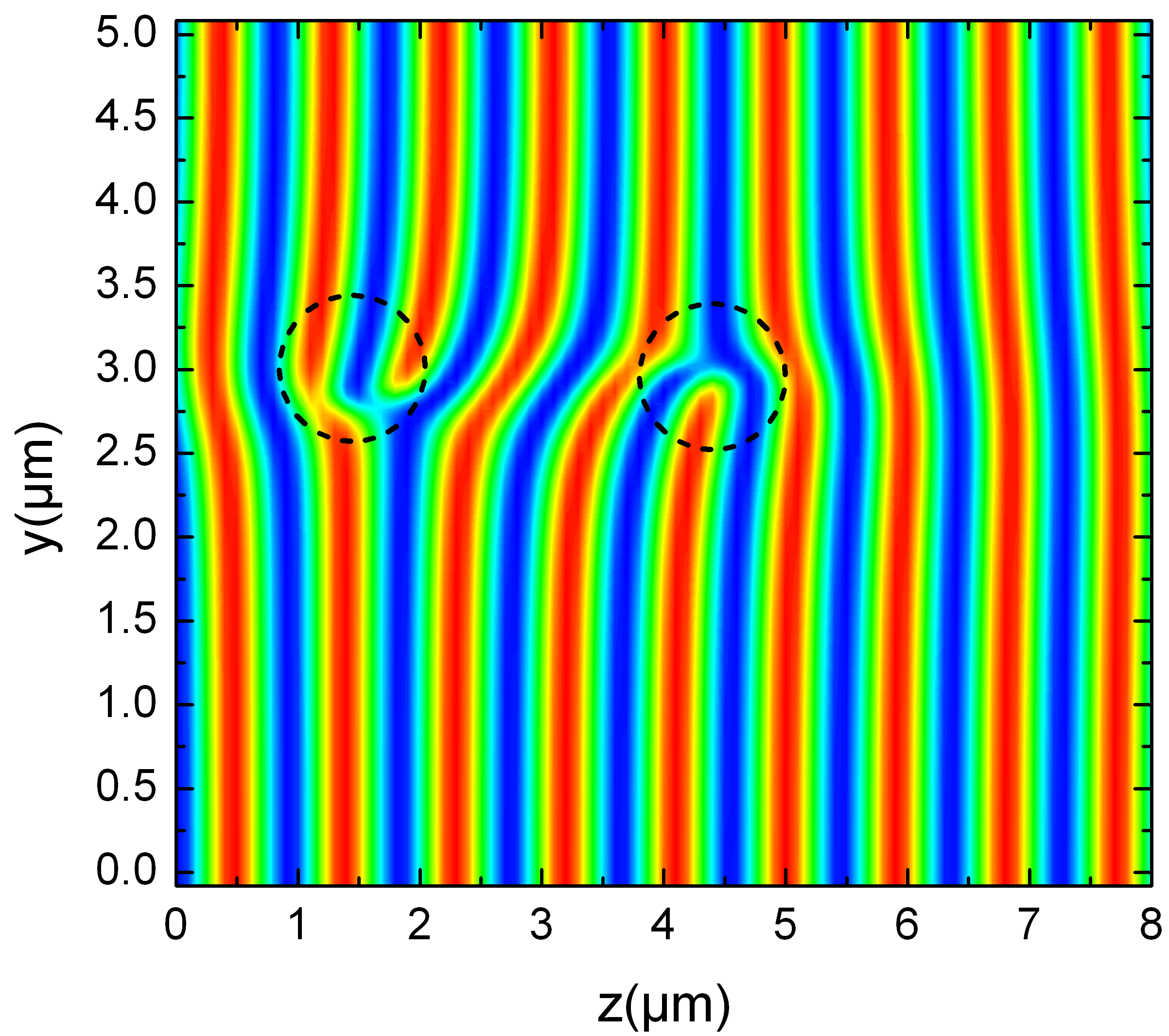
Exciton-polaritons are not the only quasi-particles in solids in which condensation has been sought or realised and I am interested in other solid-state systems that exhibit similar coherent motion, such as magnon condensates. Magnons, which are elementary excitations -- quantised spin waves -- of a magnetic system have been observed to condense in ferromagnets and in superfluid 3He-B and in compressed aerogel of superfluid 3He-A. Similar to the phases of non-condensed Bose gas, atomic spins of normal magnetic materials are in a disordered paramagnetic state. In the ordered state the spins develop the common global frequency and phase of precession. The magnon condensation of room temperature yttrium-iron garnet (YIG) films magnetised by in-plane fields is driven by microwave radiation. A microwave photon excites two primary magnons that relax forming a magnon gas with the Bose distribution. The chemical potential increases with pumping power. When the microwave power exceeds a threshold value, the magnon population condenses at finite minima of the dispersion spectrum formed by the combined effects of the exchange and magnetic dipolar interactions. I am interested in modelling these condensates and understanding the structure of the ground state and excitations such as sound waves. On this project we work in close collaboration with professor Demokritov group in Munster, Germany. |
 Optical simulators rank among the most promising candidates to power future technological breakthroughs in terms of speed, scalability, power-consumption and quantum advantage, serving a wide range of useful optimization problems.
However, the operation of such simulators remains currently limited by noise, the extent of algorithmic problems they can embed and to the classical regime where they compete with supercomputers.
HEISINGBERG aims to bring our state-of-the-art spatial photonic spin simulator (an iterated cycle of all-optical processing through a spatial light modulator that couples 10,000 spins) into the quantum regime by upgrading its coherent drive to squeezed light, making it fully programmable through vector-matrix multiplication schemes, use of holography, ancillary spins & effective magnetic fields and designing dedicated custom-tailored and purpose-built algorithms.
Optical simulators rank among the most promising candidates to power future technological breakthroughs in terms of speed, scalability, power-consumption and quantum advantage, serving a wide range of useful optimization problems.
However, the operation of such simulators remains currently limited by noise, the extent of algorithmic problems they can embed and to the classical regime where they compete with supercomputers.
HEISINGBERG aims to bring our state-of-the-art spatial photonic spin simulator (an iterated cycle of all-optical processing through a spatial light modulator that couples 10,000 spins) into the quantum regime by upgrading its coherent drive to squeezed light, making it fully programmable through vector-matrix multiplication schemes, use of holography, ancillary spins & effective magnetic fields and designing dedicated custom-tailored and purpose-built algorithms.
