Hamza Fawzi
Home Research group Publications Talks/Slides CodeResearch
My research group focusses on the design and analysis of optimization algorithms. We are primarily motivated by applications in quantum theory. See below for some of the current research projects we are involved in.Research group members:
- Ahmad Al-Sulami
- Giorgio Facelli
- Sujit Rao
Former members:
- Kun Fang (now Assistant Professor at CUHK-Shenzhen)
- Oisín Faust (now at Tower Research Capital)
- Samuel O. Scalet (now at UC Davis)
- Shengding Sun (now at LSE)
Algorithms for quantum many-body systems
A key computational task in quantum many-body theory is to determine the ground energy of an N-body system, defined as the lowest eigenvalue of the Hamiltonian operator. More generally, a fundamental quantity is the free energy of the system at temperature T > 0: \[ F(T) = -T \log \text{tr} \exp(-H/T) \] which converges to the ground energy as \(T\to0\). What makes this problem extremely challenging is that the dimensions of the Hamiltonian operator \(H\) grows exponentially with \(N\). In our research group, we seek to develop and analyze algorithms to compute the ground and free energies of quantum many-body systems using tools and ideas from convex optimization.
H. Fawzi, O. Fawzi, S. Scalet, Certified algorithms for equilibrium states of local quantum Hamiltonians, QIP'24
H. Fawzi, O. Fawzi, S. Scalet, Entropy constraints for ground state optimization, J. of Math. Phys.
H. Fawzi, O. Fawzi, S. Scalet, A subpolynomial-time algorithm for the free energy of one-dimensional quantum systems in the thermodynamic limit, ITCS'23, QIP'23

Quantum relative entropy optimization
The quantum relative entropy function plays a fundamental role in quantum information theory, and its joint convexity is a cornerstone result due to Lieb. One line of research in the group is to develop efficient and reliable numerical methods to solve optimization problems involving the quantum relative entropy function. These methods were successfully applied to problems in quantum information theory and quantum cryptography (see below).
O. Faust, H. Fawzi, J. Saunderson, A Bregman divergence view on difference of convex optimization, AISTATS’23
H. Fawzi, J. Saunderson, Optimal self-concordant barriers for quantum relative entropies, SIAM J. Optim.
H. Fawzi, J. Saunderson, P. A. Parrilo Semidefinite approximations of the matrix logarithm, Found. Comp. Math.
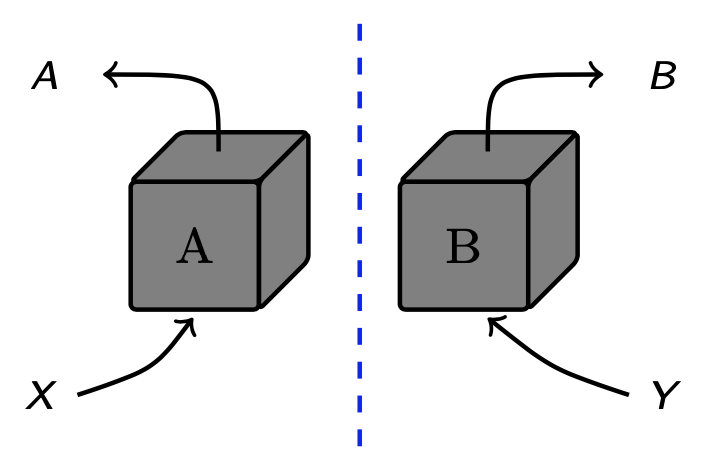
Optimization and quantum information processing
Various quantities in quantum information theory are formulated as optimization problems such as quantum channel capacities, the rate of quantum key distribution protocols, or strong data processing constants. There are many factors that make these problems challenging such as nonconvexity, infinite-dimensionality, and/or the presence of nonpolynomial functions such as the quantum entropy. In our group, we develop methods to solve such problems using ideas from semidefinite relaxations and tools from numerical analysis such as approximation theory.
O. Faust, H. Fawzi, Strong data processing inequalities via sums of squares, ISIT'22
P. Brown, H. Fawzi, O. Fawzi, Device-independent lower bounds on the conditional von Neumann entropy, QIP'22
K. Fang, H. Fawzi, The geometric Rényi divergence and its applications in quantum channel capacities, Commun. Math. Phys.
Extended formulations and conic optimization
A fundamental question in optimization theory is to characterize which convex sets admit a computationally tractable formulation. When the convex set is “complex”, a natural and very fruitful idea is to attempt to express it as the projection of a higher-dimensional convex set which is much simpler. This is called an extended formulation. One direction of research in our group is to understand the extension complexity of convex sets, and in particular the ones that arise in quantum theory, such as the set of density matrices, or the set of separable states.
H. Fawzi, J. Gouveia, P. A. Parrilo, J. Saunderson, R. Thomas, Lifting for simplicity: concise descriptions of convex sets, SIAM Rev.
H. Fawzi, The set of separable states has no finite semidefinite representation except in dimension 3x2, Commun. Math. Phys.
H. Fawzi, On polyhedral approximations of the positive semidefinite cone, Math Oper. Res.