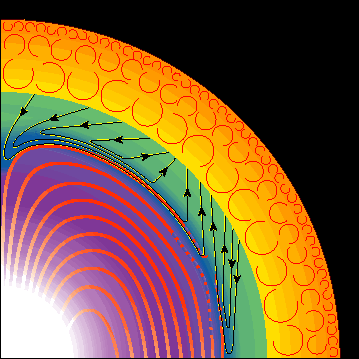

Figure 1 from Gough and McIntyre 1998, 'Inevitability of a magnetic field in the Sun's radiative interior' (Nature, 394, 755--757. The full caption is reproduced below, at the end of this page.
The full text is downloadable from here as gzipped postscript (68Kbyte), or as uncompressed postscript (326Kbyte). Here's a precursor paper supporting the `inevitability' argument (1994, The quasi-biennial oscillation (QBO): some points about the terrestrial QBO and the possibility of related phenomena in the solar interior). Two followup papers tying up the fluid-dynamical arguments including those on anti-frictional eddy motion, and drawing still stronger conclusions about tachocline and deep-interior rotation, are downloadable (1) from here and (2) from here as an acrobat (.pdf) file (0.7Mbyte). The first of these is my 2002 `Millennium' review and the second is chapter 8 in the Douglas Gough Festschrift Stellar Astrophysical Fluid Dynamics edited by M. J. Thompson and J. Christensen-Dalsgaard, copyright © Cambridge University Press, 2003, pages 111-130. Here's an animated version of Figure 8.1 of the Festschrift paper, showing an example of the real stratosphere's anti-frictional eddy motion -- a phenomenon well observed, well studied and, for more than two decades now, well understood.
More recent work has been changing aspects of the picture through various twists and turns.... here's the pdf (270K) of a preprint reporting progress up to 2006, now published as Chapter 8 in The solar tachocline, ed. D. W. Hughes, R. Rosner and N. O. Weiss, copyright © Cambridge University Press, 2007, pages 183-212. CORRIGENDUM: After equation (8.6) in the published version, please replace "where C is a constant, provided also that..." by "where C is a constant. We have also assumed that..." (It's correct in the preprint.) The chapter title is `Magnetic confinement and the sharp tachopause'.
STILL MORE RECENTLY,
Toby Wood and I discovered a new set of fully nonlinear solutions
helping to solve the
magnetic confinement problem.
They show in detail how the weak downwelling expected in high latitudes
can confine the interior field. The dynamics involves a nontrivial
interplay between microscopic magnetic diffusion and the
Lorentz and Coriolis forces. A remarkable feature of these nonlinear
confinement-layer solutions
is that the extreme smallness of the flow velocities makes the
flows likely to be
hydrodynamically and magnetohydrodynamically stable.
So although they describe very simple, strictly laminar flows
they may well provide us
with a realistic high-latitude piece of the confinement jigsaw.
A short paper presenting some of the
confinement-layer solutions (pdf, 300K)
was published in 2007, pp. 303-308 of
the proceedings of the July 2007 conference on
Unsolved Problems in Stellar Physics,
edited by R. J. Stancliffe, J. Dewi, G. Houdek, R. G. Martin,
and C. A. Tout, ISBN 978-0-7354-0462-5, ISSN 0094-243X, 465pp.,
©2007 American Institute of Physics,
AIP Conf. Proc. 948
(also arXiv:0709.1377 [astro-ph]).
CORRIGENDUM:
A coding error has been discovered which,
however, leaves the main conclusions unchanged.
Profile shapes are qualitatively the same as before,
but numerical values need changing.
The upshot is mostly to strengthen the conclusions.
In particular, there is an increase in the range of permissible downwelling
velocities U.
Also, we now know that the dynamics of the tachopause slip
layer is not Ekman-like.
These and other corrections, clarifications and extensions regarding
both the confinement-layer solutions and
the likely way they fit into a global-scale picture are
incorporated into a
 further and comprehensive paper now published in the
Journal of Fluid Mechanics,
entitled
Polar confinement of the Sun's interior magnetic
field by laminar magnetostrophic flow
(1.1 Mbyte, © 2011 Cambridge University Press,
J. Fluid Mech. 677, 445-482).
further and comprehensive paper now published in the
Journal of Fluid Mechanics,
entitled
Polar confinement of the Sun's interior magnetic
field by laminar magnetostrophic flow
(1.1 Mbyte, © 2011 Cambridge University Press,
J. Fluid Mech. 677, 445-482).
A
 survey talk trying to assess our current and prospective understanding of
tachocline fluid dynamics is
available here, complete with movies.
The title is
Tachocline fluid dynamics: an interim assessment.
survey talk trying to assess our current and prospective understanding of
tachocline fluid dynamics is
available here, complete with movies.
The title is
Tachocline fluid dynamics: an interim assessment.
The figure above (detail in green layer now superseded, but polar downwelling still, arguably, a robust feature), had the following caption in the original Nature paper. It's interesting to see how our ideas have evolved since then!
"Schematic representation of a meridional quadrant of the sun. The arrows represent the tachocline ventilation circulation, which follows surfaces S of constant specific angular momentum in the (green) body of the tachocline (whose thickness has been exaggerated by a factor 5), and is deflected by the magnetic field in the (blue) diffusive boundary layer (whose thickness has been exaggerated by a factor 50). The inclinations of the S-surfaces, which, owing to the exaggeration of the tachocline thickness, are not drawn accurately, follow from the observation that the interior angular velocity Omegai lies between the angular velocities at the equator and at the poles in the (orange) convection zone. Moreover, the centre of upwelling should be at a latitude of about 30 degrees (where, incidentally, sunspots emerge at the start of a new cycle). We are unable to draw the return flow in the convection zone without knowledge of the Reynolds stresses; details in the midlatitude upwelling region are also uncertain, obeying severely nonlinear dynamics, and may well be unsteady. The red lines represent the magnetic field in the (purple and white) radiative interior, which is assumed to be the dipole relic of a primordial field, arguably the most likely possibility (for simplicity, aligned with the rotation axis); we are unsure of the geometry of the field near the centre of upwelling, where the field lines are either dashed or absent. North-south asymmetry, as seen in the sunspot distributions observed in the Maunder minimum, may be related to the non-reversing interior dipole field. At the base of the tachocline the interior field vanishes on the rotation axis, where the magnetic boundary-layer theory suggests a singularity in the tachocline depth. The corresponding physical reality, which would again require nonlinear theory to describe it, would be relatively deep penetration of the tachocline circulation into and out of a `polar pit', which might, conceivably, extend deep enough for lithium and beryllium to be destroyed by nuclear reactions. The latest inversions of SOI seismic data suggest such a pit in the angular-velocity variation."
Note added 2010: the abovementioned paper in J. Fluid Mech. vol. 677, shows how this "pit" or, more accurately, shallow `frying pan', might be dynamically possible -- contrary to what I thought in the above `preprint reporting progress up to 2006'.