Research
Opportunities
Stay tuned for future opportunities in the group
Recent journal covers
Complex & Biological Fluids
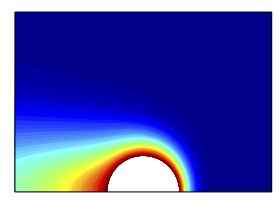

A detailed look at the biological world generates endless new problems in fluid mechanics -
new in the sense that they occur in a basic setup or regime very different from problems in the physical world.
A lot of my research activity is centered on developing quantitative models for novel questions
in biological fluid mechanics using a combination
of analytical derivations, asymptotic analysis, and numerical computations.
Past work in this area has included fluid-structure interactions at low Reynolds numbers,
many-body problems with long-range hydrodynamic interactions,
transport in non-Newtonian flows, and propulsion near boundaries.
Self-propulsion also plays an important role in the design of synthetic devices,
with bioengineering applications ranging from sensing to therapeutics.
I have in the past developed models for synthetic locomotion involving fluid motion,
including the dynamics of helical field-driven swimmers, the design of
flexible nanowire motors and their application for drug delivery, models for Marangoni transport,
friction-based locomotion, catalytic and acoustic self-propulsion, and the design of new bio-inspired pumps.
Biological Physics

Many open problems in cellular biophysics can be approached using the tools of
continuum mechanics and classical physics.
My group has been actively trying to contribute to this field, with a focus on
problems involving the interactions of cells with a viscous fluid.
Some of our past projects include the synchronization
between cellular appendages (flagella or cilia), the hydrodynamic interactions between
swimming cells and their resulting collective locomotion, the derivation of the
energetically-optimal modes of locomotion for eukaryotic and prokaryotic organisms,
and the stochastic behavior of self-propelled cells.
Physical Hydrodynamics

Flows in microfluidic devices are
dominated by the effects of geometry and surface forces. Capillarity, one of the oldest
branches of classical fluid mechanics, is relevant on length scales below millimeters.
More broadly, problems in small-scale fluid mechanics are beautiful examples of the need for an interdisciplinary approach to problem solving,
often requiring the combination of different aspects of classical physics to make new discoveries. Some of my past topics of interest
in this field include the dynamics of particle streams and suspensions, quantifying the geometry and friction of
super-hydrophobic surfaces, micro-rheology, inertia-less mixing, modelling capillary folding,
electrokinetic flows, flow stability at small scales, capillary self-assembly, and
developing new models to quantify wall slip.