Encyclopedia of Atmospheric Sciences
First Edition edited by
James R. Holton, John A. Pyle, and Judith A. Curry
and
 Second Edition edited by
Second Edition edited byGerald R. North, John A. Pyle, and Fuqing Zhang
 Second Edition edited by
Second Edition edited by(Academic Press, 2003, vol 2, pp. 680-685 and 685-694, and Elsevier 2015, vol 2, pp. 298-303 and 375-383.)
Copyright © Elsevier 2015, with special permission to
post on this website for fair use.
For the Second Edition, both articles have been substantially
revised and, I think, substantially improved. Here are reprints
 of the second edition's
Balanced Flow
and
Potential Vorticity
articles.
Again these are posted here by special permission.
of the second edition's
Balanced Flow
and
Potential Vorticity
articles.
Again these are posted here by special permission.
The balanced-flow article deals with the non-Hamiltonian velocity-splitting issue flagged below. (By contrast, the Hamiltonian velocity splitting explored in the 2002 paper by Ian Roulstone and myself has no such issues of which I'm aware; indeed, experts in the theory have long been familiar with this kind of velocity splitting, so much so that it's usually taken for granted and hardly ever mentioned, indeed often well hidden in the equations. And there is always the difficulty that the term `velocity splitting' is used with a host of other meanings. `Human language is a conceptual minefield.' However, some such terminology is still needed to express an idea that, in my opinion, is essential in order to make sense of the Hamiltonian balance theory, in the generic form originally put forward by Rick Salmon.)
For the record, the following flags up a few caveats about my articles in the First Edition, having regard to its presence in libraries.
As published in the First Edition, the two articles suffered from occasional, though mostly harmless, copy-editing damage. For instance the phrase `the submanifold in phase space' became `the in phase space submanifold' -- could the copy editor have been thinking in German? -- and the phrase `the stratospheric transport or Brewer-Dobson circulation' became `the stratospheric or transport Brewer-Dobson circulation'. (The Second Edition, by contrast, has hardly any copy-editing damage. I owe that to the very kind intervention of the Editor-in Chief.)
In June 2004, after the First Edition came out, I discovered to my embarrassment that the statement about non-Hamiltonian velocity splitting in the Balanced Flow article was wrong. (Splitting means here that the model has two velocity fields: one to advect mass, and another to advect and evaluate the exact potential vorticity.) The statement in the Balanced Flow article was true, to be sure, of all the most accurate balanced models and potential vorticity inversion operators known at the time of writing. They all exhibit velocity splitting in the sense just indicated. And it seemed to be supported by a strong heuristic argument, given in the concluding section of my paper with W. A. Norton published in 2000. In brief the argument says that, because any balanced model has to suppress the local mass rearrangement involved in the spontaneous-adjustment emission of inertia-gravity waves, there should be a tradeoff between accuracy and splitting. That is, non-Hamiltonian balanced models constrained to be free of velocity splitting should, by that fact, be unable to attain as high an accuracy as non-Hamiltonian balanced models not so constrained.
However, subsequent work with Dr A. R. Mohebalhojeh resulted in the discovery of a novel class of `hyperbalance equations', free of velocity splitting yet capable of arbitrarily high formal accuracy. The equations involve functional derivatives as well as ordinary partial derivatives. (This technicality perhaps explains why the hyperbalance equations remained undiscovered for so long.)
Very careful numerical work by Dr Mohebalhojeh then showed that the hyperbalance equations are capable of extraordinarily high numerical accuracy as well. High formal accuracy does not, of course, necessarily imply high numerical accuracy. But from extensive numerical tests it appeared that there is, after all, no systematic tradeoff between accuracy and splitting, for non-Hamiltonian balanced models.
Though surprising and embarrassing to me personally, this was excellent news theoretically. It seems that in the hyperbalance equations we now have in our possession what had long seemed an unattainable prize -- a class of non-Hamiltonian potential-vorticity-conserving balanced models competitive with all known such models in terms of accuracy, yet also (because the splitting is healed) having an exactly conserved potential enstrophy, and exact conservation of all the other non-Hamiltonian Casimirs. This work was published in June 2007 as a pair of papers in J. Atmos. Sci 64, 1782-1793 and 1794-1810. Pdf reprints are available here (copyright © American Meteorological Society): Hyperbalance Equations Part I (0.2 Mbyte), Hyperbalance Equations Part II (2.6 Mbyte). A short paper in vol. 15 of ADGEO (Advances in Geosciences), 2008, pp.47-56, gives a brief summary of the hyperbalance equations (.pdf, 0.16 Mbyte).
These results are for the shallow-water equations only. It remains possible that a tradeoff between accuracy and splitting will be found for 2-layer and multi-layer models. Related issues of balance, imbalance, slow quasimanifold etc. are discussed in a paper in the J. Atmos. Sci. Special Collection on `Spontaneous Imbalance', entitled Spontaneous imbalance and hybrid vortex-gravity structures (.pdf, 0.7 Mbyte).
The first-edition Potential Vorticity article had an extra accompanying figure, reproduced here:
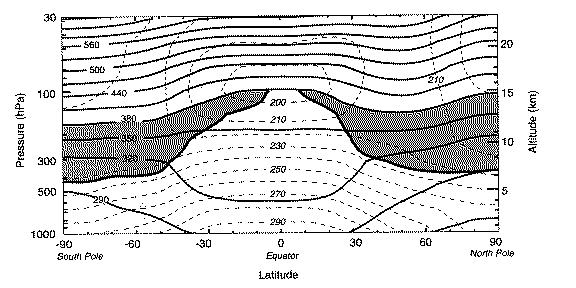
Latitude-altitude cross-section for January 1993 showing the monthly and zonally averaged temperature as dashed contours, and potential temperature as light solid contours. The heavy solid contour shows the nominal extratropical tropopause as defined by the 2 PVU contour of the Rossby-Ertel PV field calculated from Rossby's formula (3), using zonally averaged potential temperature, horizontal wind and pressure/height fields obtained from UK Met Office analyses. From the review by Holton et al., Revs. Geophys., 33, 403-439 (1995) on Stratosphere-troposphere exchange, to which the reader is referred for further detail.