(GIF Created by Philip Sellars)
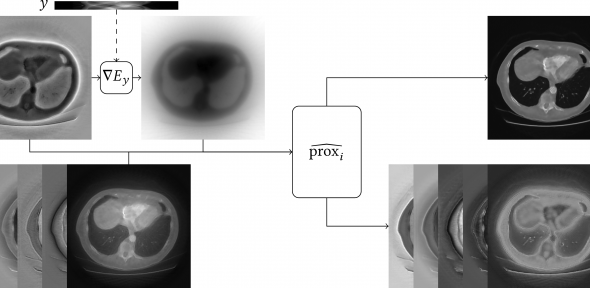
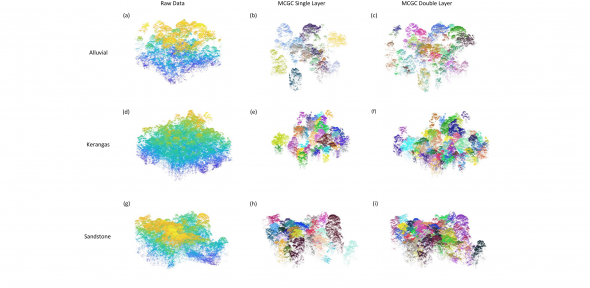
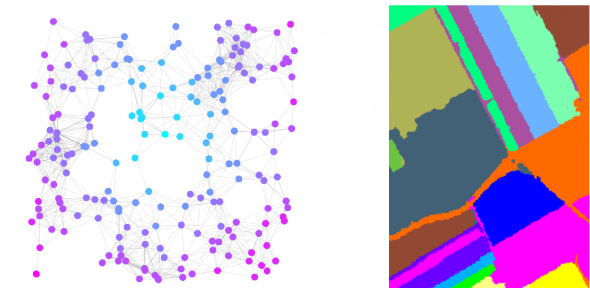
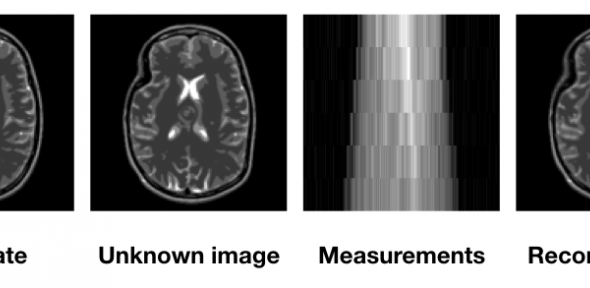
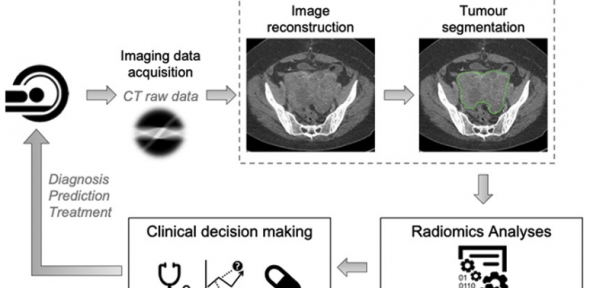
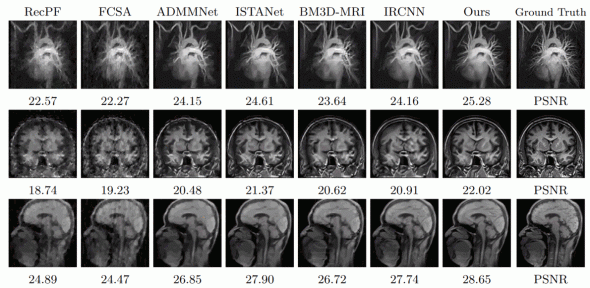
We are interested in all aspects of mathematical imaging: the use of mathematical techniques to analyse and to improve real-world images, ranging from photographs made with consumer cameras to the images made with professional imaging devices in the sciences and medicine. These include techniques such as MRI (magnetic resonance imaging) and PET (positron emission tomography). Our current research concentrates in particular on higher order PDEs for image inpainting, and discontinuity-preserving higher-order variational approaches for the recovery of sparsely sampled data. Further themes include parameter learning, with the goal of building "black box" imaging tools suitable for use by non-professionals.
Listed below are ongoing and previous projects in alphabetical order as well as funding sources. For categorised projects, follow the links on the left.