University of Cambridge  >  DAMTP  >  Goldstein Lab  >  Research

 

Goldstein Lab

Research (since ~2006)


Overview

When asked whether I am a theorist or an experimentalist, my reply is that I am a scientist. Our group seeks to understand fundamental principles that govern the behavior of nonequilibrium systems in physics and biology, using a combination of experiment and theory. This research is not easily described by a single, conventional academic label; rather, it involves the domains of condensed matter physics, physical chemistry, biological physics, fluid dynamics, applied mathematics, and geophysics.  I subscribe to Poincaré's motivation:

The scientist does not study nature because it is useful;
he studies it because he delights in it, and he delights in it because
it is beautiful. If nature were not beautiful, it would not be worth knowing, and
if nature were not worth knowing, life would not be worth living.

I also believe that some of the best science is close to art, and that Glenn Gould captured this spirit when he said

The purpose of art is not the release of a momentary ejection of adrenaline but rather the gradual,
lifelong construction of a state of wonder and serenity.

Current research in my group falls into two broad categories: Biological Physics and Natural Pattern Formation.

I. Biological Physics

Our group is currently focused on a range of questions centred around the origins of multicellularity. We use extensively the Volvocine green algae as a class of model organisms to understand the driving force behind the emergence of germ-soma differentiation, the nature of flagellar synchronization, the mechanisms of phototaxis, and basic aspects of biological fluid dynamics. A parallel set of investigations on the phenomenon of cytoplasmic streaming aims to answer the basic question of its biological purpose. Here we use the Characean algae as model organisms, and also have a developing collaboration involving streaming in the developing fruit fly oocyte.



Swimming, Stirring, and Scaling in the Volvocales

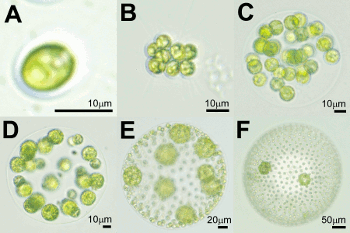One of the most fundamental issues in biology is the nature of evolutionary transitions from single cell organisms to multicellular ones. It is a general rule of nature that larger organisms are more complex, at least as measured by the number of distinct types of cells present. This reflects the fitness advantage conferred by a division of labor among specialized cells over homogeneous totipotency. Yet, increasing size has both costs and benefits, and the search for the driving forces behind the evolution of multicellularity is becoming a very active area of research. Not surprisingly for microscopic life in a fluid environment, many of the processes involved are related to transport and locomotion, for efficient exchange of chemical species with the environment is one of the most basic features of life. We study these issues using as model organisms the Volvocales, which comprise algae ranging from Chlamydomonas (A), swimming single cells, to coenobia of undifferentiated cells, such as Gonium (B) and Pandorina (C), to Volvox sp. (E,F), where the surface is covered by thousands of flagellated somatic cells, while the interior contains a far smaller number of gonidia. The existence of these closely related species allows one to study some of the most basic questions in the evolution of multicellularity. What determines the length scale or the cell number at which germ-soma differentiation appears? How do simple multicellular (or colonial) organisms lacking a central nervous system achieve the apparently coordinated motion they exhibit? What developmental program leads to the long-range cellular orientation observed in the larger species? Our first two works in this area laid the groundwork for many of these issues by developing micromanipulation and fluid dynamical methods of studying the flagella-driven flows in these organisms, thereby establishing the high Péclet numbers found in these systems and showing through experiment and theory that such flows can remove what would otherwise be a diffusional bottleneck in nutrient uptake limiting viability of the larger species.
[back to overview]

Tracking Protists in Three Dimensions

Many flagellated protists display swimming behavior that is inherently three dimensional, and a number of important questions in biology and physics are associated with how the motion of such organisms is related to their body plan and to external stimuli such as light, dissolved molecular species, gravity, temperature, boundaries, and electromagnetic fields. It is thus desirable to track their position and orientation in 3D with high spatiotemporal resolution and, unless desired, free from systematic bias introduced by external stimuli, background fluid motion, and hydrodynamic surface effects. We have developed such an apparatus, optimized for tracking swimming micro-organisms in the size range of 10-1000 microns, in three dimensions, far from surfaces, and with negligible background convective fluid motion. Charge coupled device cameras attached to two long working distance microscopes synchronously image the sample from two perpendicular directions, with narrow band dark-field or bright-field illumination chosen to avoid triggering a phototactic response. The images from the two cameras can be combined to yield 3D tracks of the organism. Using additional, highly directional broad-spectrum illumination with millisecond timing control the phototactic trajectories in 3D of organisms ranging from Chlamydomonas to Volvox can be studied in detail. Surface-mediated hydrodynamic interactions can also be investigated without convective interference. Minimal modifications to the apparatus allow for studies of chemotaxis and other taxes.
[back to overview]

Hydrodynamic Bound States of Swimming Algae

Because of its bottom-heaviness, in the absence of phototactic cues Volvox swims upward against gravity. Using glass chambers we discovered that when nearby colonies reach the chamber ceiling they are attracted together and can form a stable bound state in which they "waltz" around each other. The attractive interaction was shown to be a surface-mediated effect associated with the density offset of the colonies relative to water (so that in the far-field each is described by a downward-pointing Stokeslet), in the presence of a no-slip wall. Quantitative agreement with experimental observations on infalling trajectories was achieved with no free parameters. Lubrication theory for the dynamics of nearby spinning, bottom-heavy colonies can be used to explain the orbiting dynamics of the bound states. A second "minueting" dynamics occurs with older colonies that hover near the lower chamber wall. These phenomena are suggested to underlie observed clustering of Volvox at surfaces.
[back to overview]

Synchronization of Eukaryotic Flagella

The coordination of eukaryotic flagella is essential for many of the most basic processes of life (motility, sensing, and development), yet its emergence and regulation and its connection to locomotion are poorly understood. Previous studies show that the unicellular alga and Chlamydomonas reinhardtii, widely regarded as an ideal system in which to study flagellar biology, swims forward by the synchronous action of its two flagella. Using high-speed imaging over long intervals, we found a richer behavior: A cell swimming in the dark stochastically switches between synchronous and asynchronous flagellar beating. The synchronous state is interrupted stochastically by phase slips. The dynamics of slips and the statistics of phase-locked intervals are consistent with a low-dimensional stochastic model of hydrodynamically coupled oscillators, with a noise amplitude set by the intrinsic fluctuations of single flagellar beats. Three-dimensional tracking shows that the alternation between synchronous and asynchronous beating regimes leads, respectively, to nearly straight swimming and to abrupt large reorientations, which yield a eukaryotic version of the "run-and-tumble" motion of peritrichously flagellated bacteria.
[back to overview]

Fidelity of Adaptive Phototaxis

Along the evolutionary path from single cells to multicellular organisms with a central nervous system are species of intermediate complexity that move in ways suggesting high-level coordination, yet have none. Instead, organisms of this type possess many autonomous cells endowed with programs that have evolved to achieve concerted responses to environmental stimuli. In our recent paper experiment and theory are used to develop a quantitative understanding of how cells of such organisms coordinate to achieve phototaxis, by using the colonial alga Volvox carteri as a model. It is shown that the surface somatic cells act as individuals but are orchestrated by their relative position in the spherical extracellular matrix and their common photoresponse function to achieve colony-level coordination. Analysis of models that range from the minimal to the biologically faithful shows that, because the flagellar beating displays an adaptive down-regulation in response to light, the colony needs to spin around its swimming direction and that the response kinetics and natural spinning frequency of the colony appear to be mutually tuned to give the maximum photoresponse. These models further predict that the phototactic ability decreases dramatically when the colony does not spin at its natural frequency, a result confirmed by phototaxis assays in which colony rotation was slowed by increasing the fluid viscosity.
[back to overview]

Emergence of Synchronized Beating During the Regrowth of Eukaryotic Flagella

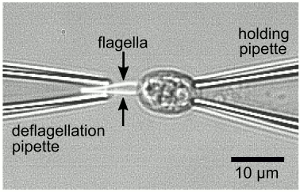A fundamental issue in the biology of eukaryotic flagella is the origin of synchronized beating observed in tissues and organisms containing multiple flagella. Our recent studies of the biflagellate unicellular alga Chlamydomonas reinhardtii provided the first evidence that the interflagellar coupling responsible for synchronization is of hydrodynamic origin. To investigate this mechanism in detail we have studied synchronization in Chlamydomonas as its flagella slowly regrow after mechanically-induced self-scission. The duration of synchronized intervals is found to be strongly dependent on flagellar length. Analysis within a stochastic model of coupled phase oscillators is used to extract the length dependence of the interflagellar coupling and the intrinsic beat frequencies of the two flagella. Physical and biological considerations that may explain these results are proposed.

Anomalous Tracer Statistics in Active Suspensions

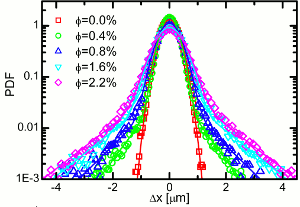In contexts such as suspension feeding in marine ecologies there is an interplay between Brownian motion of nonmotile particles and their advection by flows from swimming microorganisms. One appealing point of view is that the sea of swimming organisms constitutes an effective "thermal bath" analogous to the multitudes of molecules responsible for Brownian motion, where each encounter of a tracer particle with a swimmer provides a random kick. In conventional Brownian motion, e.g., with micron-size particles in water, there is an enormous separation of time scales between the duration of molecular collisions (ps) and the observed particle motion (ms). In contrast, in a suspension of microorganisms it is possible to resolve the encounters with tracer particles, and the dynamical problem involves correlated advective trajectories in the presence of true Brownian noise. As a laboratory realization of this, we have studied passive tracers in suspensions of eukaryotic swimmers, the alga Chlamydomonas reinhardtii. While the cells behave ballistically over short intervals, the tracers behave diffusively, with a time-dependent but self-similar probability distribution function of displacements consisting of a Gaussian core and robust exponential tails. We emphasize the role of flagellar beating in creating oscillatory flows that exceed Brownian motion far from each swimmer.
[back to overview]

Direct Measurements of the Flow Fields Around Swimming Microorganisms

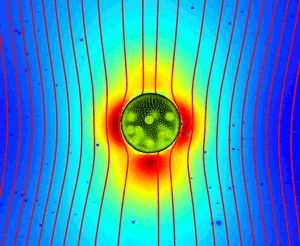Swimming microorganisms create flows that influence their mutual interactions and modify the rheology of their suspensions. While extensively studied theoretically, these flows have not been measured in detail around any freely-swimming microorganism. Using a synthesis of tracking microscopy, particle imaging velocimetry, and particle tracking velocimetry, we achieved such measurements for the microphytes Volvox carteri, and Chlamydomonas reinhardtii. The minute (~0.3%) density excess of V. carteri over water leads to a strongly dominant Stokeslet contribution, with the widely-assumed stresslet flow only a correction to the subleading source dipole term. This implies that suspensions of V. carteri have features similar to suspensions of sedimenting particles (see the next section for an explanation of the consequences of this). The flow in the region around C. reinhardtii where significant hydrodynamic interaction is likely to occur differs qualitatively from a puller stresslet, and can be described by a simple three-Stokeslet model.
[back to overview]

Fluid Dynamics and Noise in Bacterial Cell-Cell and Cell-Surface Interactions

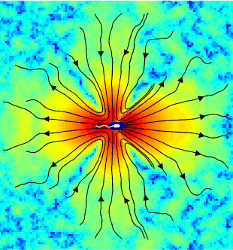Bacterial processes ranging from gene expression to motility and biofilm formation are constantly challenged by internal and external noise. While the importance of stochastic fluctuations has been appreciated for chemotaxis, it is currently believed that deterministic long-range fluid dynamical effects govern cell-cell and cell-surface scattering, the elementary events that lead to swarming and collective swimming in active suspensions and to the formation of biofilms. We have succeeded in making the first direct measurements of the bacterial flow field generated by individual swimming Escherichia coli both far from and near to a solid surface. These experiments allowed us to examine the relative importance of fluid dynamics and rotational diffusion for bacteria. For cell-cell interactions it is shown that thermal and intrinsic stochasticity drown the effects of long-range fluid dynamics, implying that physical interactions between bacteria are determined by steric collisions and near-field lubrication forces. This dominance of short-range forces closely links collective motion in bacterial suspensions to self-organization in driven granular systems, assemblages of biofilaments, and animal flocks. For the scattering of bacteria with surfaces, long-range fluid dynamical interactions are also shown to be negligible before collisions; however, once the bacterium swims along the surface within a few microns after an aligning collision, hydrodynamic effects can contribute to the experimentally observed, long residence times. Because these results are based on purely mechanical properties, they apply to a wide range of microorganisms.
[back to overview]

Fluid Velocity Fluctuations in a Suspension of Swimming Protists

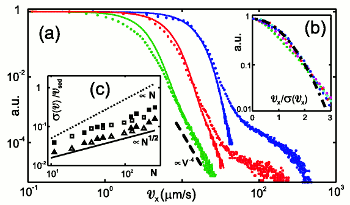In dilute suspensions of swimming microorganisms the local fluid velocity is a random superposition of the flow fields set up by the individual organisms, which in turn have multipole contributions decaying as inverse powers of distance from the organism. We have studied the relationship between the decay exponent of the dominant multipole contribution and the statistics of velocity fluctuations, and derived the conditions under which the central limit theorem guarantees a Gaussian probability distribution function of velocities are satisied. This holds when the leading force singularity is a Stokeslet, but not when it is any higher multipole. These results are confirmed by numerical studies and by experiments on suspensions of the alga Volvox carteri, which show that deviations from Gaussianity arise from near-field effects. Such observations are complementary to the observation (see above) of non-Gaussian finite-time particle displacement distribution functions in suspensions of C. reinhardtii.
[back to overview]

Physics and Biology of Cytoplasmic Streaming

Since Bonaventura Corti's discovery in 1774 of the persistent circulation of the cytoplasm of plant cells, the phenomenon now known as cytoplasmic streaming or cyclosis has been conjectured to play an important role in metabolism. It occurs in organisms as diverse as amoebae, algae and terrestrial plants, and fungi. In plants it is driven by multitudes of the motor protein myosin moving along bundled actin at the boundary of the cytoplasm, carrying microscopic particles or organelles, and entraining fluid. The motion of protoplasmic granules entrained in the flow includes unidirectional streaming, "fountain streaming" (in which the motion near the central axis of the cell is opposite to that near the periphery), and spiral "rotational streaming." The fact that transport by fluid motion becomes necessary to outrun the slow pace of diffusion in larger organisms, as emphasized in the celebrated essay by Haldane on size in biology, has been a theme in discussions of cytoplasmic streaming for many years. Yet, there has been little theoretical work and fewer experiments that have quantified the full implications of cytoplasmic streaming for transport and mixing. We have embarked on a research program aimed at answering some of the most basic open questions in this field: What purpose does cytoplasmic streaming have in cells? How does it impact on homeostasis and development? What gives rise to the often complex flow geometries found in streaming?
[back to overview]

Microfluidics of Cytoplasmic Streaming

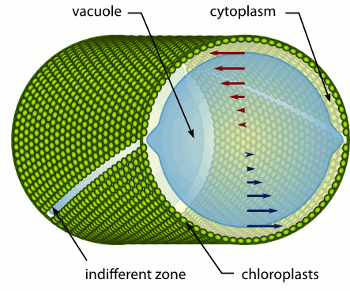In the more than two centuries since its discovery, streaming has frequently been conjectured to aid in transport and mixing of molecular species in the cytoplasm and, by implication, in cellular homeostasis, yet no theoretical analysis has been presented to quantify these processes. We show by solution of the coupled dynamics of fluid flow and diffusion appropriate to the archetypal "rotational streaming" of algal species such as Chara and Nitella that internal mixing and the transient dynamical response to changing external conditions can indeed be enhanced by streaming, but to an extent that depends strongly on the pitch of the helical flow. The possibility that this may have a developmental consequence is illustrated by the coincidence of the exponential growth phase of Nitella and the point of maximum enhancement of those processes. Key to these results is the discovery and analysis of a circulatory flow transverse to the cylinder's long axis, akin to Dean vortices at finite Reynolds numbers, which arises from the chiral geometry. Strongly enhanced lateral transport and longitudinal homogenization occur if the transverse Péclet number is sufficiently large, with scaling laws arising from boundary layers.
[back to overview]

Measurement of Cytoplasmic Streaming by Magnetic Resonance Velocimetry

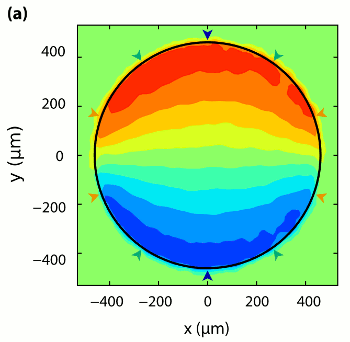In the giant cylindrical cells found in Characean algae, multitudes of the molecular motor myosin transport the cytoplasm along opposing spiralling bands covering the inside of the cell wall, generating a helical shear flow in the large central vacuole. It has been suggested that such flows enhance mixing within the vacuole and thereby play a role in regulating metabolism. For this to occur the membrane that encloses the vacuole, namely the tonoplast, must transmit efficiently the hydrodynamic shear generated in the cytoplasm. Existing measurements of streaming flows are of insufficient spatial resolution and extent to provide tests of fluid mechanical theories of such flows and information on the shear transmission. We have used magnetic resonance velocimetry (MRV) to obtain the first measurements of cytoplasmic streaming velocities in single living cells. The spatial variation of the longitudinal velocity field in cross-sections of internodal cells of Chara corallina was obtained and shown to be in quantitative agreement with our theoretical analysis of rotational cytoplasmic streaming driven by bidirectional helical forcing in the cytoplasm, with direct shear transmission by the tonoplast.
[back to overview]

Shear-Driven Circulation Patterns in Lipid Membrane Vesicles

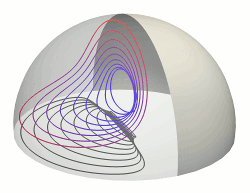Recent experiments have shown that when a hemispherical lipid vesicle attached to a solid surface is subjected to a simple shear flow it exhibits a pattern of membrane circulation much like a dipole vortex. This is in marked contrast to the toroidal circulation that would occur in the related problem of a drop of immiscible fluid attached to a surface and subjected to shear. This profound difference in floow patterns arises from the lateral incompressibility of the membrane, which restricts the observable flows to those in which the velocity field in the membrane is two-dimensionally divergence free, so there is no return flow to the bulk. We have studied these circulation patterns within the simplest model of membrane fluid dynamics. A systematic expansion of the flow field based on Papkovich-Neuber potentials is developed for general viscosity ratios between the membrane and the surrounding fluids. Comparison with experimental results [C. Vezy, G. Massiera, and A. Viallat, Soft Matter 3, 844 (2007)] is made, and it is shown how such studies can allow measurements of the membrane viscosity. Issues of symmetry-breaking and pattern selection are discussed.
[back to overview]

Fluctuations, Dynamics, and the Stretch-Coil Transition of Single Actin Filaments in Extensional Flows

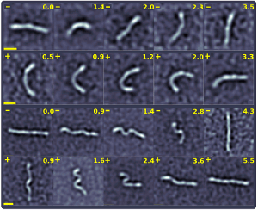Recent work on the motion of elastic filaments subject to hydrodynamic forces has revealed complex nonlinear dynamics in the neighborhood of hyperbolic stagnation points in the flow. Unlike the simpler orbits of rigid elongated objects in the presence of shear and vorticity, these dynamics arise from the tension induced in the filament by an extensional flow, which beyond a critical value can induce an instability analogous to Euler buckling of a filament with thrust at its two ends. This predicted `stretch-coil' transition, which is complementary to the `coil-stretch' transition of exible polymers, has recently been observed with macroscopic fibers in cellular flows generated by electrodynamic forcing. Motivated by the role that semiflexible polymers subject to hydrodynamic forcing play in cytoskeletal motions in the cell, particularly when filaments guide molecular motors whose motions create flows, we have used a microfluidic cross-flow geometry to provide the first comprehensive study of the interplay between tension, fluctuations, and buckling of biopolymers, including a fluctuation-rounded stretch-coil transition of actin filaments.
[back to overview]

Coupling of Active Motion and Advection Shapes Intracellular Cargo Transport

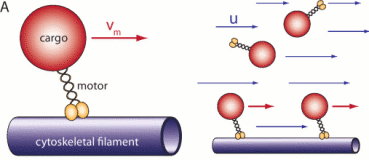Intracellular cargo transport can arise from passive diffusion, active motor-driven transport along cytoskeletal filament networks, and passive advection by fluid flows entrained by such motor/cargo motion. Active and advective transport are thus intrinsically coupled as related, yet different representations of the same underlying network structure. We have used a reaction-advection-diffusion system to show that this coupling affects the transport and localization of a passive tracer in a confined geometry. For sufficiently low diffusion, cargo localization to a target zone is optimized either by low reaction kinetics and decoupling of bound and unbound states, or by a mostly disordered cytoskeletal network with only weak directional bias. These generic results may help to rationalize subtle features of cytoskeletal networks, for example as observed for microtubules in fly oocytes.
[back to overview]

Cytoplasmic Streaming in Drosophila Oocytes Varies with Kinesin
Activity and Correlates with the Microtubule Cytoskeleton Architecture

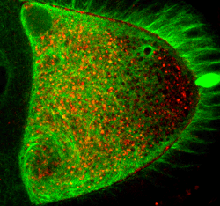Cells can localize molecules asymmetrically through the combined action of cytoplasmic streaming, which circulates their fluid contents, and specific anchoring mechanisms. Streaming also contributes to the distribution of nutrients and organelles such as chloroplasts in plants, the asymmetric position of the meiotic spindle in mammalian embryos, and the developmental potential of the zygote, yet little has been known quantitatively about the relationship between streaming and the motor activity which drives it. In a collaboration with Dr. Isabel Palacios and her student Dr. Lucy S. Williams (Zoology, Cambridge) we have used Particle Image Velocimetry (PIV) to quantify the statistical properties of Kinesin-dependent streaming during mid-oogenesis in Drosophila. We find that streaming can be used to detect subtle changes in Kinesin activity and that the flows reflect the architecture of the microtubule cytoskeleton. Furthermore, based on characterization of the rheology of the cytoplasm in vivo, we establish estimates of the number of Kinesins required to drive the observed streaming. Using this in vivo data as the basis of a model for transport, we suggest that the disordered character of transport at mid-oogenesis, as revealed by streaming, is an important component of the localization dynamics of the body plan determinant oskar mRNA.
[back to overview]

Spontaneous Circulation in Confined Active Suspensions

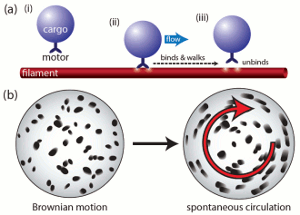Many active fluid systems encountered in biology are set in total geometric confinement. Cytoplasmic streaming in plant cells is a prominent and ubiquitous example, in which cargo-carrying molecular motors move along polymer filaments and generate cell-scale flow. When filaments are not fixed to the cell periphery, a situation found both in vivo and in vitro, we observe that the basic dynamics of streaming are closely related to those of a nonmotile stresslet suspension. Under this model, we have demonstrated that confinement makes possible a stable circulating state; a linear stability analysis reveals an activity threshold for spontaneous autocirculation. Numerical analysis of the longtime behavior reveals a phenomenon akin to defect separation in nematic liquid crystals and a high-activity bifurcation to an oscillatory regime. These observations provide a possible interpretation to the experiments of Yotsuyanagi from 1953, in which drops of cytoplasm extracted from the aquatic plant Chara were observed over time to undergo a transition from disordered random internal motion to organized persistent circulation.
[back to overview]

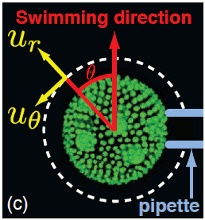Metachronal Waves on Volvox carteri

From unicellular ciliates to the respiratory epithelium, carpets of cilia display metachronal waves, long-wavelength phase modulations of the beating cycles. A large body of theoretical work over the past few decades has suggested that these waves may arise from hydrodynamic coupling between the beating flagella. Experimental study of this phenomenon has been limited by a lack of organisms for which the flagella and the flows they create can be visualized with ease. Using time-resolved particle image velocimetry and micropipette manipulation, we report the discovery of metachronal waves on the surface of the colonial alga Volvox carteri, whose large size and ease of growth and visualization make it an ideal model organism for these studies. The flagella of Volvox are relatively far apart compared to the celebrated ciliate Paramecium, and thus more nearly in the weak-coupling limit amenable to theory. V. carteri robustly displays symplectic metachronal waves, those for which the wave propagation direction is that of the power stroke of each flagellum. An elastohydrodynamic model of weakly coupled compliant oscillators, recast as interacting phase oscillators, reveals that orbit compliance can produce fast, robust synchronization in a manner essentially independent of boundary conditions, and offers an intuitive understanding of a possible mechanism leading to the emergence of metachronal waves.
[back to overview]

Antiphase Flagellar Synchronization

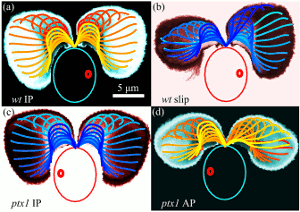Groups of beating flagella or cilia often synchronize so that neighboring filaments have identical frequencies and phases. A prime example is provided by the unicellular biflagellate Chlamydomonas reinhardtii, which typically displays synchronous in-phase beating in a low-Reynolds number version of breaststroke swimming. It is known that steering by flagella during phototaxis is a consequence of `flagellar dominance', namely that the two flagella exhibit different responses to intracellular calcium levels produced by the photoresponse. The mutant ptx1 is a flagellar dominance mutant in which the asymmetric response is absent. We report the discovery that ptx1, can exhibit synchronization in precise antiphase, as in the freestyle swimming stroke. High-speed imaging shows that ptx1 flagella switch stochastically between in-phase and antiphase states, and that the latter has a distinct waveform and significantly higher frequency, both of which are strikingly similar to those found during phase slips that stochastically interrupt in-phase beating of the wild type. Possible mechanisms underlying these observations are discussed.
[back to overview]

The Many `Phases' of Coupled Flagella

In a multitude of life's processes, cilia and flagella are found indispensable. Recently, the biflagellated chlorophyte alga Chlamydomonas has become a model organism for the study of ciliary motility and synchronization. Here, we use high-speed, high-resolution imaging of single pipette-held cells to quantify the rich dynamics exhibited by their flagella. Underlying this variability in behaviour are biological dissimilarities between the two flagella -- termed cis and trans, with respect to a unique eyespot. With emphasis on the wildtype, we derive limit cycles and phase parameterizations for self-sustained flagellar oscillations from digitally-tracked flagellar waveforms. Characterizing interflagellar phase-synchrony via a simple model of coupled oscillators with noise, we find that during the canonical swimming breaststroke the cis flagellum is consistently phase-lagged relative to, whilst remaining robustly phase-locked with, the trans flagellum. Transient loss of synchrony, or phase-slippage, may be triggered stochastically, in which the trans flagellum transitions to a second mode of beating with attenuated beat-envelope and increased frequency. Further, exploiting this alga's ability for flagellar regeneration, we mechanically induced removal of one or the other flagellum of the same cell to reveal a striking disparity between the beating of the cis vs trans flagellum, in isolation. These results are evaluated in the context of the dynamic coordination of Chlamydomonas flagella.
[back to overview]

Rheotaxis Facilitates Upstream Navigation of Mammalian Sperm Cells

A major puzzle in biology is how mammalian sperm determine and maintain the correct swimming direction during the various phases of the sexual reproduction process. Whilst chemotaxis is assumed to dominate in the immediate vicinity of the ovum, it is unclear which biochemical or physical cues guide spermatozoa on their long journey towards the egg cell. Currently debated mechanisms range from peristaltic pumping to temperature sensing (thermotaxis) and direct response to fluid flow variations (rheotaxis), but little is known quantitatively about their relative importance. We report the first quantitative experimental study of mammalian sperm rheotaxis. Using microfluidic devices, we investigate systematically the swimming behavior of human and bull sperm over the whole range of physiologically relevant shear rates and viscosities. Our measurements show that the interplay of fluid shear, steric surface-interactions and chirality of the flagellar beat leads to a stable upstream spiraling motion of sperm cells, thus providing a generic and robust rectification mechanism to support mammalian fertilisation. To rationalise these findings, we identify a minimal mathematical model that is capable of describing quantitatively the experimental observations. The combined experimental and theoretical evidence supports the hypothesis that the shape and beat patterns of mammalian sperm cells have evolved to optimally exploit rheotaxis for long-distance navigation.
[back to overview]

Fluid Flows Created by Swimming Bacteria Drive Self-Organization in Confined Suspensions

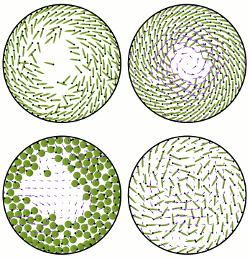Concentrated suspensions of swimming microorganisms and other forms of active matter are known to display complex, self-organized spatio-temporal patterns on scales large compared to those of the individual motile units. Despite intensive experimental and theoretical study, it has remained unclear the extent to which the hydrodynamic flows generated by swimming cells, rather than purely steric interactions between them, drive the self-organization. We utilize the recent discovery of a spiral-vortex state in confined suspensions of B. subtilis to study this issue in detail. Those experiments showed that if the radius of confinement in a thin cylindrical chamber is below a critical value the suspension will spontaneously form a steady single-vortex state encircled by a counter-rotating cell boundary layer, with spiral cell orientation within the vortex. Left unclear, however, was the flagellar orientation, and hence the cell swimming direction, within the spiral vortex. Here, using a fast simulation method that captures oriented cell-cell and cell-fluid interactions in a minimal model of discrete-particle systems, we predict the striking, counterintuitive result that in the presence of collectively-generated fluid motion the cells within the spiral vortex actually swim upstream against those flows. This is then confirmed by new experiments reported here, which include measurements of flagella bundle orientation and cell tracking in the self-organized state. These results highlight the complex interplay between cell orientation and hydrodynamic flows in concentrated suspensions of microorganisms.
[back to overview]

Flagellar Synchronization Through Direct Hydrodynamic Interactions

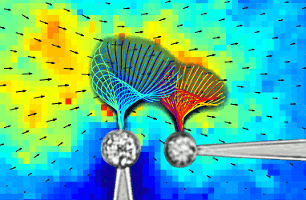Flows generated by ensembles of flagella are crucial to development, motility and sensing, but the mechanisms behind this striking coordination remain unclear. We present novel experiments in which the two micropipette-held somatic cells of Volvox carteri, with distinct intrinsic beating frequencies, are studied by high-speed imaging as a function of their separation and orientation. Analysis of time series shows that the interflagellar coupling, constrained by lack of connections between cells to be hydrodynamical, exhibits a spatial dependence consistent with theory. At close spacings it produces robust synchrony for thousands of beats, while at increasing separations synchrony is degraded by stochastic processes. Manipulation of the relative flagellar orientation reveals in-phase and antiphase states, consistent with dynamical theories. Flagellar tracking with exquisite precision reveals waveform changes that result from hydrodynamic coupling. This study proves unequivocally that flagella coupled solely through a fluid can achieve robust synchrony despite differences in their intrinsic properties.
[back to overview]

How a Volvox Embryo Turns Itself Inside Out

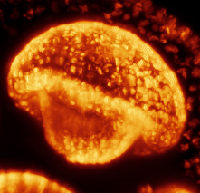Deformations of cell sheets are ubiquitous in early animal development, often arising from a complex and poorly understood interplay of cell shape changes, division, and migration. A prime example of this type of phenomenon is gastrulation, the process in early embryonic development in which an initially spherical mass of cells develops an invagination that leads eventually to the formation of the gastric system, and a change of topology to toroidal. In order to begin to unravel the separate contributions to such folding events, we have explored perhaps the simplest example of cell sheet folding: the "inversion" process of the algal genus Volvox, during which spherical embryos turn themselves inside out through a process hypothesized to arise from cell shape changes alone. We have used light sheet microscopy to obtain the first four-dimensional (3 space + time) visualizations of so-called type-B inversion in the species Volvox globator, from which it is possible make detailed quantitative measurements of many relevant geometry quantities. In this work, we also proposed the first mathematical theory of this process, in which cell shape changes appear as local variations of intrinsic curvature, contraction and stretching of a thin elastic shell. Our results support a scenario in which these active processes function in a defined spatiotemporal manner to enable inversion.

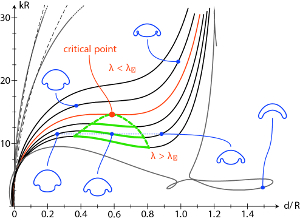Subsequent work on type B inversion explored in detail the continuum model, which is based on the biological features of cell shape changes and changes in the location of intercellular cytoplasmic bridges, which hold the sheet together. When those bridges connect the midpoints of adjacent cells in a sheet, then cells that become tall and thin produce contraction of the cell sheet area, while those that become short and squat produce expansion. When cells become elongated and the bridges migrate to the cell tips, as is known to be the case during initiation of inversion, then a preferred curvature is created. We have explored the sequence of quasistatic equilibria that occur when a wave of such changes progresses around the colony, coupled with anterior expansion and posterior contraction. When all three occur in the right spatio-temporal sequence, inversion can occur smoothly. This work also revealed an interesting bifurcation structure in the parameter space, and the possibility of multiple coexisting shapes. A generalization of the problem to type-A inversion has also been developed, addressing the bending and peeling of elastic "lips".
[back to overview]

Cortical Microtubule Nucleation Can Organise the Cytoskeleton of Drosophila Oocytes to Define the Anteroposterior Axis

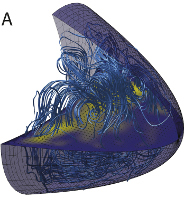Many cells contain non-centrosomal arrays of microtubules (MTs), but the assembly, organisation and function of these arrays are poorly understood. We present the first theoretical model for the non-centrosomal MT cytoskeleton in Drosophila oocytes, in which bicoid and oskar mRNAs become localised to establish the anterior-posterior body axis. Constrained by experimental measurements, the model shows that a simple gradient of cortical MT nucleation is sufficient to reproduce the observed MT distribution, cytoplasmic flow patterns and localisation of oskar and naive bicoid mRNAs. Our simulations exclude a major role for cytoplasmic flows in localisation and reveal an organisation of the MT cytoskeleton that is more ordered than previously thought. Furthermore, modulating cortical MT nucleation induces a bifurcation in cytoskeletal organisation that accounts for the phenotypes of polarity mutants. Thus, our three-dimensional model explains many features of the MT network and highlights the importance of differential cortical MT nucleation for axis formation.
[back to overview]

Motility of Colonial Choanoflagellates and the Statistics of Aggregate Random Walkers

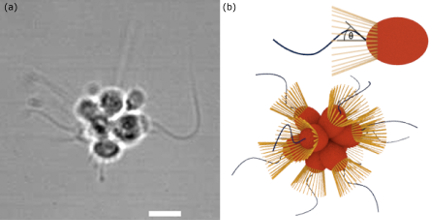We illuminate the nature of the three-dimensional random walks of microorganisms composed of individual organisms adhered together. Such aggregate random walkers are typified by choanoflagellates, eukaryotes that are the closest living relatives of animals and have emerged as as important model organisms in the study of the evolution of multicellularity. In the colony-forming species Salpingoeca rosetta, which consists of cells oriented roughly radially, with flagella pointing outwards and the cell body inward, we show that the beating of each flagellum is stochastic and uncorrelated with others within the colony. Moreover, the vectorial sum of the flagellar propulsion forces and torques results in residuals of each that lead to stochastic helical swimming. A quantitative theory for these results is presented and species variability discussed.
[back to overview]

Ferromagnetic and Antiferromagnetic Order in Bacterial Vortex Lattices

Despite their inherently non-equilibrium nature, living systems can self-organize in highly ordered collective states that share striking similarities with the thermodynamic equilibrium phases of conventional condensed-matter and fluid systems. Examples range from the liquid-crystal-like arrangements of bacterial colonies, microbial suspensions and tissues to the coherent macro-scale dynamics in schools of fish and flocks of birds. Yet, the generic mathematical principles that govern the emergence of structure in such artificial and biological systems are elusive. It is not clear when, or even whether, well-established theoretical concepts describing universal thermostatistics of equilibrium systems can capture and classify ordered states of living matter. Here, we connect these two previously disparate regimes: through microfluidic experiments and mathematical modelling, we demonstrate that lattices of hydrodynamically coupled bacterial vortices can spontaneously organize into distinct patterns characterized by ferro- and antiferromagnetic order. The coupling between adjacent vortices can be controlled by tuning the inter-cavity gap widths. The emergence of opposing order regimes is tightly linked to the existence of geometry-induced edge currents, reminiscent of those in quantum systems. Our experimental observations can be rationalized in terms of a generic lattice field theory, suggesting that bacterial spin networks belong to the same universality class as a wide range of equilibrium systems.
[back to overview]

Coordinated Beating of Algal Flagella is Mediated by Basal Coupling

Cilia and flagella often exhibit synchronized behavior; this includes phase locking, as seen in Chlamydomonas, and metachronal wave formation in the respiratory cilia of higher organisms. Since the observations by Gray and Rothschild of phase synchrony of nearby swimming spermatozoa, it has been a working hypothesis that synchrony arises from hydrodynamic interactions between beating filaments. Recent work on the dynamics of physically separated pairs of flagella isolated from the multicellular alga Volvox has shown that hydrodynamic coupling alone is sufficient to produce synchrony. However, the situation is more complex in unicellular organisms bearing few flagella. We show that flagella of Chlamydomonas mutants deficient in filamentary connections between basal bodies display markedly different synchronization from the wild type. We perform micromanipulation on configurations of flagella and conclude that a mechanism, internal to the cell, must provide an additional flagellar coupling. In naturally occurring species with 4, 8, or even 16 flagella, we find diverse symmetries of basal body positioning and of the flagellar apparatus that are coincident with specific gaits of flagellar actuation, suggesting that it is a competition between intracellular coupling and hydrodynamic interactions that ultimately determines the precise form of flagellar coordination in unicellular algae.
[back to overview]

Directed Collective Motion of Bacteria Under Channel Confinement

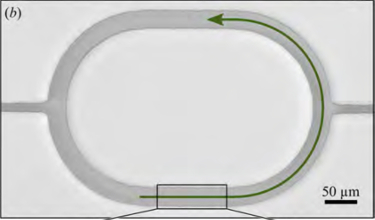Dense suspensions of swimming bacteria are known to exhibit collective behaviour arising from the interplay of steric and hydrodynamic interactions. Unconfined suspensions exhibit transient, recurring vortices and jets, whereas those confined in circular domains may exhibit order in the form of a spiral vortex. Here, we show that confinement into a long and narrow macroscopic "racetrack" geometry stabilises bacterial motion to form a steady unidirectional circulation. This motion is reproduced in simulations of discrete swimmers that reveal the crucial role that bacteria-driven fluid flows play in the dynamics. In particular, cells close to the channel wall produce strong flows which advect cells in the bulk against their swimming direction. We examine in detail the transition from a disordered state to persistent directed motion as a function of the channel width, and show that the width at the crossover point is comparable to the typical correlation length of swirls seen in the unbounded system. Our results shed light on the mechanisms driving the collective behaviour of bacteria and other active matter systems, and stress the importance of the ubiquitous boundaries found in natural habitats.
[back to overview]

Filter-Feeding, Near-field Flows, and the Morphologies of Colonial Choanoflagellates

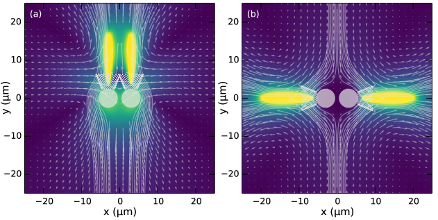Efficient uptake of prey and nutrients from the environment is an important component in the fitness of all microorganisms, and its dependence on size may reveal clues to the origins of evolutionary transitions to multicellularity. Because potential benefits in uptake rates must be viewed in the context of other costs and benefits of size, such as varying predation rates and the increased metabolic costs associated with larger and more complex body plans, the uptake rate itself is not necessarily that which is optimized by evolution. Uptake rates can be strongly dependent on local organism geometry and its swimming speed, providing selective pressure for particular arrangements. Here, we examine these issues for choanoflagellates, filter-feeding microorganisms that are the closest relatives of the animals. We explore the different morphological variations of the choanoflagellate Salpingoeca rosetta, which can exist as a swimming cell, as a sessile thecate cell, and as colonies of cells in various shapes. In the absence of other requirements and in a homogeneously nutritious environment, we find that the optimal strategy to maximize filter-feeding by the collar of microvilli is to swim fast, which favors swimming unicells. In large external flows, the sessile thecate cell becomes advantageous. Effects of prey diffusion are discussed and also found to be to the advantage of the swimming unicell.
[back to overview]

Elastohydrodynamic Synchronization of Adjacent Beating Flagella

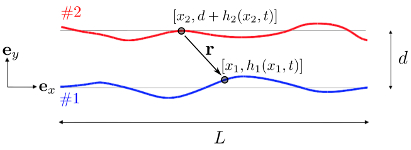It is now well established that nearby beating pairs of eukaryotic flagella or cilia typically synchronize in phase. A substantial body of evidence supports the hypothesis that hydrodynamic coupling between the active filaments, combined with waveform compliance, provides a robust mechanism for synchrony. This elastohydrodynamic mechanism has been incorporated into bead-spring models in which the beating flagella are represented by microspheres tethered by radial springs as they are driven about orbits by internal forces. While these low-dimensional models reproduce the phenomenon of synchrony, their parameters are not readily relatable to those of the filaments they represent. More realistic models, which reflect the underlying elasticity of the axonemes and the active force generation, take the form of fourth-order nonlinear partial differential equations (PDEs). While computational studies have shown the occurrence of synchrony, the effects of hydrodynamic coupling between nearby filaments governed by such continuum models have been examined theoretically only in the regime of interflagellar distances d large compared to flagellar length L. Yet in many biological situations d/L≪1. Here we present an asymptotic analysis of the hydrodynamic coupling between two extended filaments in the regime d/L≪1 and find that the form of the coupling is independent of the microscopic details of the internal forces that govern the motion of the individual filaments. The analysis is analogous to that yielding the localized induction approximation for vortex filament motion, extended to the case of mutual induction. In order to understand how the elastohydrodynamic coupling mechanism leads to synchrony of extended objects, we introduce a heuristic model of flagellar beating. The model takes the form of a single fourth-order nonlinear PDE whose form is derived from symmetry considerations, the physics of elasticity, and the overdamped nature of the dynamics. Analytical and numerical studies of this model illustrate how synchrony between a pair of filaments is achieved through the asymptotic coupling.
[back to overview]

Aerotaxis in the Closest Relatives of Animals

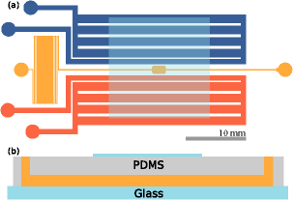As the closest unicellular relatives of animals, choanoflagellates serve as useful model organisms for understanding the evolution of animal multicellularity. An important factor in animal evolution was the increasing ocean oxygen levels in the Precambrian, which are thought to have influenced the emergence of complex multicellular life. As a first step in addressing these conditions, we study here the response of the colony-forming choanoflagellate Salpingoeca rosetta to oxygen gradients. Using a microfluidic device that allows spatio-temporal variations in oxygen concentrations, we report the discovery that S. rosetta displays positive aerotaxis. Analysis of the spatial population distributions provides evidence for logarithmic sensing of oxygen, which enhances sensing in low oxygen neighborhoods. Analysis of search strategy models on the experimental colony trajectories finds that choanoflagellate aerotaxis is consistent with stochastic navigation, the statistics of which are captured using an effective continuous version based on classical run-and-tumble chemotaxis.
[back to overview]

Spontaneous Oscillation of Elastic Filaments Induced by Molecular Motors

It is known from the wave-like motion of microtubules in motility assays that the piconewton forces that motors produce can be sufficient to bend the filaments. In cellular phenomena such as cytosplasmic streaming, molecular motors translocate along cytoskeletal filaments, carrying cargo which entrains fluid. When large numbers of such forced filaments interact through the surrounding fluid, as in particular stages of oocyte development in Drosophila melanogaster, complex dynamics are observed, but the detailed mechanics underlying them has remained unclear. Motivated by these observations, we study perhaps the simplest model for these phenomena: an elastic filament, pinned at one end, acted on by a molecular motor treated as a point force. Because the force acts tangential to the filament, no matter what its shape, this "follower-force" problem is intrinsically non-variational, and thereby differs fundamentally from Euler buckling, where the force has a fixed direction, and which, in the low-Reynolds-number regime, ultimately leads to a stationary, energy-minimizing shape. Through a combination of linear stability theory, analytical study of a solvable simplified "two-link" model and numerical studies of the full elastohydrodynamic equations of motion, we elucidate the Hopf bifurcation that occurs with increasing forcing of a filament, leading to flapping motion analogous to the high-Reynolds-number oscillations of a garden hose with a free end.
[back to overview]

Mutualism Between Microbial Populations in Structured Environments: The Role of Geometry in Diffusive Exchanges

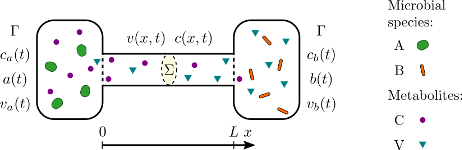The exchange of diffusive metabolites is known to control the spatial patterns formed by microbial populations, as revealed by recent studies in the laboratory. However, the matrices used, such as agarose pads, lack the structured geometry of many natural microbial habitats, including in the soil or on the surfaces of plants or animals. Here we address the important question of how such geometry may control diffusive exchanges and microbial interaction. We model mathematically mutualistic interactions within a minimal unit of structure: two growing reservoirs linked by a diffusive channel through which metabolites are exchanged. The model is applied to study a synthetic mutualism, experimentally parametrized on a model algal-bacterial co-culture. Analytical and numerical solutions of the model predict conditions for the successful establishment of remote mutualisms, and how this depends, often counterintuitively, on diffusion geometry. We connect our findings to understanding complex behavior in synthetic and naturally occurring microbial communities.
[back to overview]

The Role of Tumbling Frequency and Persistence in Optimal Run-and-Tumble Chemotaxis

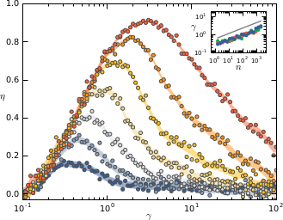One of simplest examples of navigation found in nature is run-and-tumble chemotaxis. Tumbles reorient cells randomly, and cells can drift towards attractants or away from repellents by biasing the frequency of these events. The post-tumble swimming directions are typically correlated with those prior, as measured by the variance of the reorientation angle distribution. This variance can range from large, in the case of bacteria, to so small that tumble events are imperceptible as observed in choanoflagellates. This raises the question of optimality: why is such a range of persistence observed in nature? Here, we study persistent run-and-tumble dynamics, focusing first on the optimization of the linearized chemotactic response within the 2D parameter space of tumble frequency and angular persistence. Although an optimal persistence does exist for a given tumble frequency, in the full parameter space there is a continuum of optimal solutions. Introducing finite tumble times that depend on the persistence can change this picture, illuminating one possible method for selecting tumble persistence based on species-specific reorientation dynamics. Moving beyond linear theory we find that optimal chemotactic strengths exist, and that these maximize reaction when swimming in a wrong direction but have little or no reaction when swimming with even the slightest projection along the chemoattractant gradient.
[back to overview]

The Noisy Basis of Morphogenesis: Mechanisms and Mechanics of Cell Sheet Folding Inferred from Developmental Variability

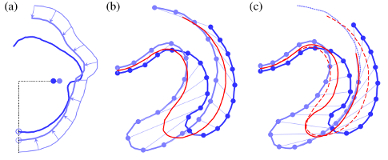Variability is emerging as an integral part of development. It is therefore imperative to ask how to access the information contained in this variability. Yet most studies of development average their observations and, discarding the variability, seek to derive models, biological or physical, that explain these average observations. Here, we analyse this variability in a study of cell sheet folding in the green alga Volvox, whose spherical embryos turn themselves inside out in a process sharing invagination, expansion, involution, and peeling of a cell sheet with animal models of morphogenesis. We generalise our earlier, qualitative model of the initial stages of inversion by combining ideas from morphoelasticity and shell theory. Together with three-dimensional visualisations of inversion using light sheet microscopy, this yields a detailed, quantitative model of the entire inversion process. With this model, we show how the variability of inversion reveals that two separate, temporally uncoupled processes drive the initial invagination and subsequent expansion of the cell sheet. This implies a prototypical transition towards higher developmental complexity in the volvocine algae and provides proof of principle of analysing morphogenesis based on its variability.
[back to overview]

Time-Irreversibility and Criticality in the Motility of a Flagellate Microorganism

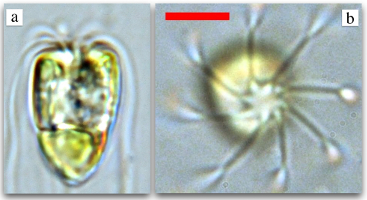Active living organisms exhibit behavioral variability, partitioning between fast and slow dynamics. Such variability may be key to generating rapid responses in a heterogeneous, unpredictable environment wherein cellular activity effects continual exchanges of energy fluxes. We demonstrate a novel, noninvasive strategy for revealing nonequilibrium control of swimming - specifically, in an octoflagellate microalga. These organisms exhibit surprising features of flagellar excitability and mechanosensitivity, which characterize a novel, time-irreversible "run-stop-shock" motility comprising forward runs, knee-jerk shocks with dramatic beat reversal, and long stops during which cells are quiescent yet continue to exhibit submicron flagellar vibrations. Entropy production, associated with flux cycles arising in a reaction graph representation of the gait-switching dynamics, provides a direct measure of detailed balance violation in this primitive alga.
[back to overview]

Evaporation-Driven Convective Flows in Suspensions of Non-Motile Bacteria

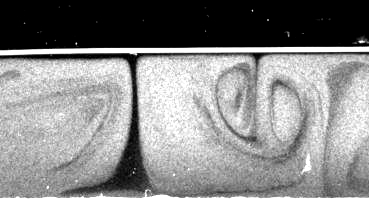We report a novel form of convection in suspensions of the bioluminescent marine bacterium Photobacterium phosphoreum. Suspensions of these bacteria placed in a chamber open to the air create persistent luminescent plumes most easily visible when observed in the dark. These flows are strikingly similar to the classical bioconvection pattern of aerotactic swimming bacteria, which create an unstable stratification by swimming upwards to an air-water interface, but they are a puzzle since the strain of P. phosphoreum used does not express flagella and therefore cannot swim. When microspheres were used instead of bacteria, similar flow patterns were observed, suggesting that the convective motion was not driven by bacteria but instead by the accumulation of salt at the airwater interface due to evaporation of the culture medium. Even at room temperature and humidity, and physiologically relevant salt concentrations, the water evaporation was found to be sufficient to drive convection patterns. To prove this hypothesis, experiments were complemented with a mathematical model that aimed to understand the mechanism of plume formation and the role of salt in triggering the instability. The simplified system of evaporating salty water was first studied using linear stability analysis, and then with finite element simulations. A comparison between these three approaches is presented. While evaporation-driven convection has not been discussed extensively in the context of biological systems, these results suggest that the phenomenon may be broadly relevant, particularly in those systems involving microorganisms of limited motility.
[back to overview]


II. Natural Pattern Formation

We have a longstanding interest in instabilities and pattern formation in geophysical systems, dynamics of interfaces, and aspects of the statistical physics of fibrous materials. This work often combines aspects of differential geometry and nonlinear dynamics.

The Shape of a Ponytail and the Statistical Physics of Hair Fiber Bundles

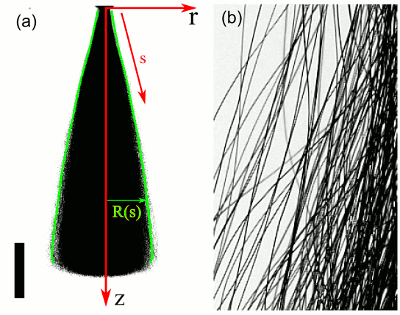A bundle of hair, whether a paintbrush or a ponytail, adopts a shape determined by the interplay of the stiffness and weight of the individual fibers and their intrinsic waviness or curliness. Since a typical bundle may have ten thousand individual hairs, each with a distinct profile of intrinsic curvatures, the determination of its shape is a problem in the statistical physics of disordered systems. In work with Patrick B. Warren and Robin C. Ball we have developed a variational theory for the properties of hair bundles. The theory is based on the local density and mean orientation of hairs, with the effects of random curvatures subsumed into a local energy functional. This decomposition reveals how the concept of an `equation of state' of hair appears naturally in the force balance that governs the equilibrium shape of the bundle. Specializing to long, narrow, axisymmetric bundles, an ansatz of self-similarity allows the many-body problem to be reduced to an equivalent single-fiber one for the envelope of the bundle. The interplay between filament stiffness and weight, and the pressure arising from random curvatures defines two main regimes of ponytail shapes. This reduction in turn allows the equation of state of hair to be determined from measurements of ponytail shapes. A robust image-processing method for determining the three-dimensional shapes of individual hairs and a procedure for extracting the envelope of a bundle are described in detail. Measurements of those properties for commercially-available hair switches are presented, and it is shown that the equation of state thus determined is essentially Hookean, with a spring constant determined by the bending elasticity and the spectrum of random curvatures of individual fibers.
[back to overview]

A Ratchet Trap for Leidenfrost Droplets

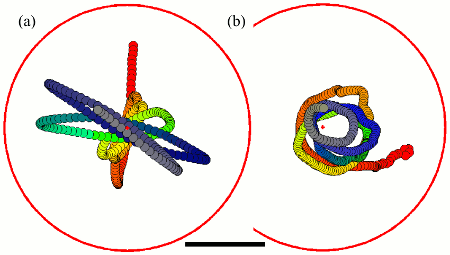When a Leidenfrost drop is levitated above a surface with parallel asymmetric sawtooth-shaped ridges it is known to be propelled in a unique direction by the interaction of the vapour layer with the surface. We have exploited this effect to construct a `ratchet trap' for Leidenfrost drops: a surface with concentric circular ridges, each asymmetric in cross section. A combination of experiment and theory is used to study the dynamics of drops in these traps, whose centre is a stable fixed point. Numerical analysis of the vapour flow over a ratchet surface suggests new insights into the mechanism of motion rectification that are incorporated into the simplest equations of motion for ratchet-driven motion of a Leidenfrost body; these resemble a central force problem in celestial mechanics with mass loss and drag. A phase plane analysis of experimental trajectories is used to extract more detailed information about the ratcheting phenomenon. Orbiting drops are found to exhibit substantial deformations; those with large internal angular momentum can even undergo binary fission. Such ratchet traps may thus prove useful in the controlled study of many properties of Leidenfrost drops.
[back to overview]

Topological Transitions of Minimal Surfaces

It is well known that a soap film spanning a looped wire can have the topology of a Möbius strip and that deformations of the wire can induce a transformation to a two-sided film, but the process by which this transformation is achieved has remained unknown. We have studied this problem by experiment and theory and found that the process consists of a collapse of the film toward the boundary that produces a previously unrecognized finite-time twist singularity that changes the linking number of the film's Plateau border and the centerline of the wire. A movie of this fascinating phenomenon is here. We conjecture that it is a general feature of this type of transition that the singularity always occurs at the surface boundary. The change in linking number is shown to be a consequence of a viscous reconnection of the Plateau border at the moment of the singularity. High-speed imaging of the collapse dynamics of the film's throat, similar to that of the central opening of a catenoid, reveals a crossover between two power laws. Far from the singularity, it is suggested that the collapse is controlled by dissipation within the fluid film surrounding the wire, whereas closer to the transition the power law has the classical form arising from a balance between air inertia and surface tension. Analytical and numerical studies of minimal surfaces and ruled surfaces are used to gain insight into the energetics underlying the transition and the twisted geometry in the neighborhood of the singularity.
[back to overview]

Boundary Singularities Produced by the Motion of Soap Films

Recent work has shown that a Möbius strip soap film rendered unstable by deforming its frame changes topology to that of a disk through a `neck-pinching' boundary singularity. This behaviour is unlike that of the catenoid, which transitions to two disks through a bulk singularity. It is not yet understood whether the type of singularity is generally a consequence of the surface topology, nor how this dependence could arise from an equation of motion for the surface. To address these questions we investigated experimentally, computationally, and theoretically the route to singularities of soap films with different topologies, including a family of punctured Klein bottles. We show that the location of singularities (bulk or boundary) may depend on the path of the boundary deformation. In the unstable regime the driving force for soap-film motion is the mean curvature. Thus, the narrowest part of the neck, associated with the shortest nontrivial closed geodesic of the surface, has the highest curvature and is the fastest-moving. Just before onset of the instability there exists on the stable surface a shortest closed geodesic, which is the initial condition for evolution of the neck's geodesics, all of which have the same topological relationship to the frame. We make the plausible conjectures that if the initial geodesic is linked to the boundary then the singularity will occur at the boundary, whereas if the two are unlinked initially then the singularity will occur in the bulk. Numerical study of mean curvature flows and experiments support these conjectures.
[back to overview]

Instability of a Gravity Current Within a Soap Film

One of the simplest geometries in which to study fluid flow between two soap films connected by a Plateau border is provided by a catenoid with a secondary film at its narrowest point. Dynamic variations in the spacing between the two rings supporting the catenoid lead to fluid flow between the primary and secondary films. When the rings are moved apart, while keeping their spacing within the overall stability regime of the films, after a rapid thickening of the secondary film the excess fluid in it starts to drain into the sloped primary film through the Plateau border at which they meet. This influx of fluid is accommodated by a local thickening of the primary film. Experiments described here show that after this drainage begins the leading edge of the gravity current becomes linearly unstable to a finite-wavelength fingering instability. A theoretical model based on lubrication theory is used to explain the mechanism of this instability. The predicted characteristic wavelength of the instability is shown to be in good agreement with experimental results. Since the gravity current advances into a film of finite, albeit microscopic, thickness this situation is one in which the regularization often invoked to address singularities at the nose of a thin film is physically justified.
[back to overview]

Coiling, Entrainment, and Synchronization of Viscous Fluid Jets

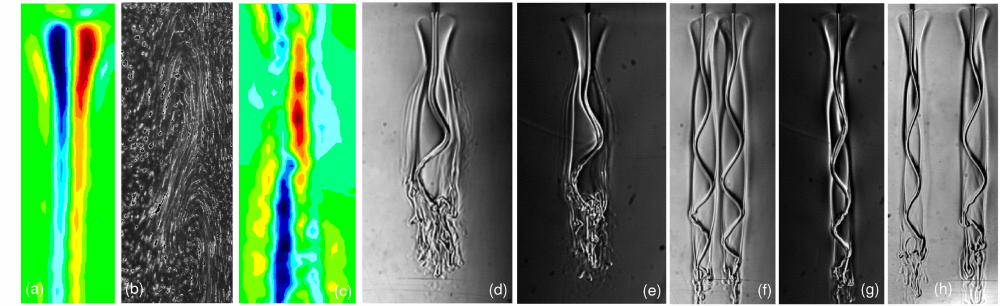From algal suspensions to magma upwellings and galactic dynamics one finds fluid jets which exhibit complex symmetry-breaking instabilities as they are decelerated by their surroundings. We have studied the simplest system that captures this complexity yet allows direct experimental control; a saline jet descending through a salinity gradient.  The descending jet coils like a corkscrew within a conduit of viscously entrained fluid whose upward recirculation braids the jet. The underlying jet structure and certain scaling relations can be understood through similarity solutions to the fluid equations and the physics of Kelvin-Helmholtz instabilities. The image shows vorticity maps (color) obtained from PIV with suspended microspheres that illustrate the recirculating flow within the conduit in a time-averaged manner (left) and instantaneously (right), and a streak photograph (b) offering another view of the swirling flows that braid the coiling jet.  Panels (d,e) and (f,g) show from and side views of two interacting jets that are, respectively, sharing a single conduit and just further apart than a conduit width.  In the latter case, the jets synchronize as mirror-images.   Panel h reveals that when jets are even further apart they nest together.   More recently we have done extensive numerical and analytical work on the underlying mechanism of the instability in a two-dimensional version of this problem.
[back to overview]

Speleothem Morphology

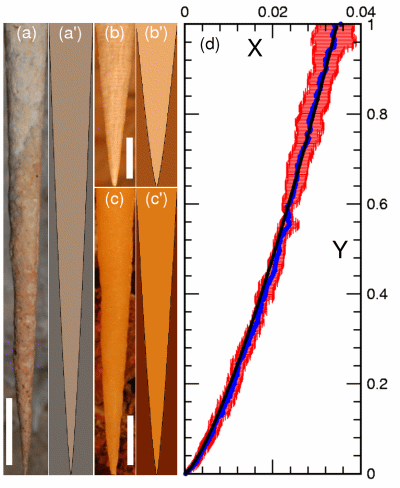The chemical mechanisms underlying the growth of cave formations such as stalactites are well-known, yet no theory had been proposed which successfully accounts for the dynamic evolution of their shapes. We have developed such a theory (see also a longer paper) that considers the interplay of thin-film fluid dynamics, calcium carbonate chemistry, and CO2 transport in the cave to show that stalactites evolve according to a novel local geometric growth law which exhibits extreme amplification at the tip as a consequence of the locally-varying fluid layer thickness. Studies of this model show that a broad class of initial conditions is attracted to an ideal shape which is strikingly close to a statistical average of natural stalactites. This ideal shape has the remarkable property of being completely parameter-free, save for an overall scaling, as for the Platonic ideals like the circle and the square. The figure shows (left) three examples of natural stalactites in Kartchner Caverns (Benson, AZ) and the ideal shape which most closely matches them. At the right is a composite average shape (in blue, with statistical uncertainties in red) compared with our calculated Platonic ideal of stalactites (black). The agreement is striking. We are currently extending these ideas to understand non-axisymmetric shapes found in caves and the surface ripple instability commonly seen.
[back to overview]

Icicle Morphology

In light of the results described above on stalactite growth it was natural to wonder how it is that icicles obtain their characteristic long and pointy shapes, and we have begun to investigate the growth and melting of icicles as free-boundary problems. Our first work describes perhaps the simplest synthesis of atmospheric heat transfer, geometrical considerations, and thin-film fluid dynamics. Crucial to this analysis is the power-law form of the thermal boundary layer rising upwards adjacent to the icicle surface. It acts as an insulating thermal blanket whose thickness self-consistently determines the icicle growth rate. This analysis led to the discovery of a nonlinear ordinary differential equation for the shape of a uniformly advancing icicle, the solution to which defines a parameter-free shape which compares very favorably with that of natural icicles. Away from the tip, the solution has a power-law form identical to that found for the growth of stalactites by precipitation of calcium carbonate. This analysis thereby explains why stalactites and icicles are so similar in form despite the vastly different physics and chemistry of their formation. In addition, a curious link is noted between the shape so calculated and that found through consideration of only the thin coating water layer.
[back to overview]
More recently, we have studied in a more controlled fashion the melting of a cylinder of ice in warm air in order to quantify the heat-transfer mechanisms controlling the evolution of its shape, which are inherent in a range of phenomena involving phase change and fluid flow. Motivated by the initial melting at the top of a flat-topped cylinder of ice, we analyse laminar, natural convection above a cooled, finite, horizontal plate (or below a heated, finite, horizontal plate) and show that, to a very good approximation, the partial-differential, boundary-layer equations can be separated with self-similar vertical profiles scaled by the boundary-layer thickness. We find that the horizontal evolution of the boundary-layer thickness is governed by equations describing a steady, viscous gravity current fed by diffusive entrainment, and therefore describe such flows as diffusive gravity currents. We first use the predictions of our model to examine previous experimental results in two dimensions. Our experimental results relating to the melting of ice in air are then compared with predictions based on our analysis of the axisymmetric thermal boundary layer. This comparison confirms the vertical thermal structure and shows that melting is governed in roughly equal measure by heat transfer from the air, the latent heat of condensation of water vapour, and the net radiative heat transfer from the surroundings to the ice.
[back to overview]

Instability of a Möobius Strip Minimal Surface and a Link with Systolic Geometry

We describe the first analytically tractable example of an instability of a nonorientable minimal surface under parametric variation of its boundary. A one-parameter family of incomplete Meeks Möbius surfaces is defined and shown to exhibit an instability threshold as the bounding curve is opened up from a doublecovering of the circle. Numerical and analytical methods are used to determine the instability threshold by solution of the Jacobi equation on the double covering of the surface. The unstable eigenmode shows excellent qualitative agreement with that found experimentally for a closely related surface. A connection is proposed between systolic geometry and the instability by showing that the shortest noncontractable closed geodesic on the surface (the systolic curve) passes near the maximum of the unstable eigenmode.
[back to overview]

Instabilities and Solitons in Minimal Strips

We show that highly twisted minimal strips can undergo a nonsingular transition, unlike the singular transitions seen in the Möbius strip and the catenoid. If the strip is nonorientable, this transition is topologically frustrated, and the resulting surface contains a helicoidal defect. Through a controlled analytic approximation, the system can be mapped onto a scalar ?4 theory on a nonorientable line bundle over the circle, where the defect becomes a topologically protected kink soliton or domain wall, thus establishing their existence in minimal surfaces. Demonstrations with soap films confirm these results and show how the position of the defect can be controlled through boundary deformation.
[back to overview]

Theory of Shape-Shifting Droplets

Recent studies of cooled oil emulsion droplets uncovered transformations into a host of flattened shapes with straight edges and sharp corners, driven by a partial phase transition of the bulk liquid phase. Here, we explore theoretically the simplest geometric competition between this phase transition and surface tension in planar polygons and recover the observed sequence of shapes and their statistics in qualitative agreement with experiments. Extending the model to capture some of the three-dimensional structure of the droplets, we analyze the evolution of protrusions sprouting from the vertices of the platelets and the topological transition of a puncturing planar polygon.
[back to overview]

Why Clothes Don't Fall Apart: Tension Transmission in Staple Yarns

The problem of how staple yarns, those composed of myriads of short fibers, transmit tension was first described by Galileo in the context of ropes in his Dialogues Concerning Two New Sciences (1638). We examine the mechanics of this problem using abstract models in which the Amontons-Coulomb friction laws yield a linear programing (LP) problem for the tensions in the fiber elements. We find there is a percolation transition such that above the percolation threshold the transmitted tension is in principle unbounded. We determine that the mean slack in the LP constraints is a suitable order parameter to characterize this supercritical state. We argue the mechanism is generic, and in practical terms, it corresponds to a switch from a ductile to a brittle failure mode accompanied by a significant increase in mechanical strength.
[back to overview]
 

© 2011-2019 Department of Applied Mathematics and Theoretical Physics, University of Cambridge
Information provided by R.E.Goldstein@damtp.cam.ac.uk